Chapter 3 Missing values and imputation
3.1 Load data
3.2 Examine predictor missingness
3.2.1 Missingness table
# Look at missingness among predictors.
missing = is.na(data[, vars$predictors])
# This will be a zero-row tibble if there is no missingness in the data.
missing_df =
data.frame(var = colnames(missing),
missing_mean = colMeans(missing),
missing_count = colSums(missing)) %>%
filter(missing_count > 0) %>% arrange(desc(missing_mean))
missing_df## var missing_mean missing_count
## oldpeak oldpeak 0.02310231 7
## ca ca 0.01980198 6
## thal thal 0.01980198 6
## age age 0.01650165 5
## restecg restecg 0.01650165 5
## cp cp 0.01320132 4
## fbs fbs 0.01320132 4
## slope slope 0.01320132 4
## chol chol 0.00990099 3
## thalach thalach 0.00990099 3
## sex sex 0.00660066 2
## exang exang 0.00330033 1if (nrow(missing_df) == 0) {
cat("No missinginess found in the predictors.")
} else {
missing_df$missing_mean = paste0(round(missing_df$missing_mean * 100, 1), "%")
missing_df$missing_count = prettyNum(missing_df$missing_count, big.mark = ",")
colnames(missing_df) = c("Variable", "Missing rate", "Missing values")
print({ kab_table = kable(missing_df, format = "latex", digits = c(0, 3, 0),
booktabs = TRUE) })
cat(kab_table %>% kable_styling(latex_options = "striped"),
file = "tables/missingness-table.tex")
}##
## \begin{tabular}{llll}
## \toprule
## & Variable & Missing rate & Missing values\\
## \midrule
## oldpeak & oldpeak & 2.3\% & 7\\
## ca & ca & 2\% & 6\\
## thal & thal & 2\% & 6\\
## age & age & 1.7\% & 5\\
## restecg & restecg & 1.7\% & 5\\
## \addlinespace
## cp & cp & 1.3\% & 4\\
## fbs & fbs & 1.3\% & 4\\
## slope & slope & 1.3\% & 4\\
## chol & chol & 1\% & 3\\
## thalach & thalach & 1\% & 3\\
## \addlinespace
## sex & sex & 0.7\% & 2\\
## exang & exang & 0.3\% & 1\\
## \bottomrule
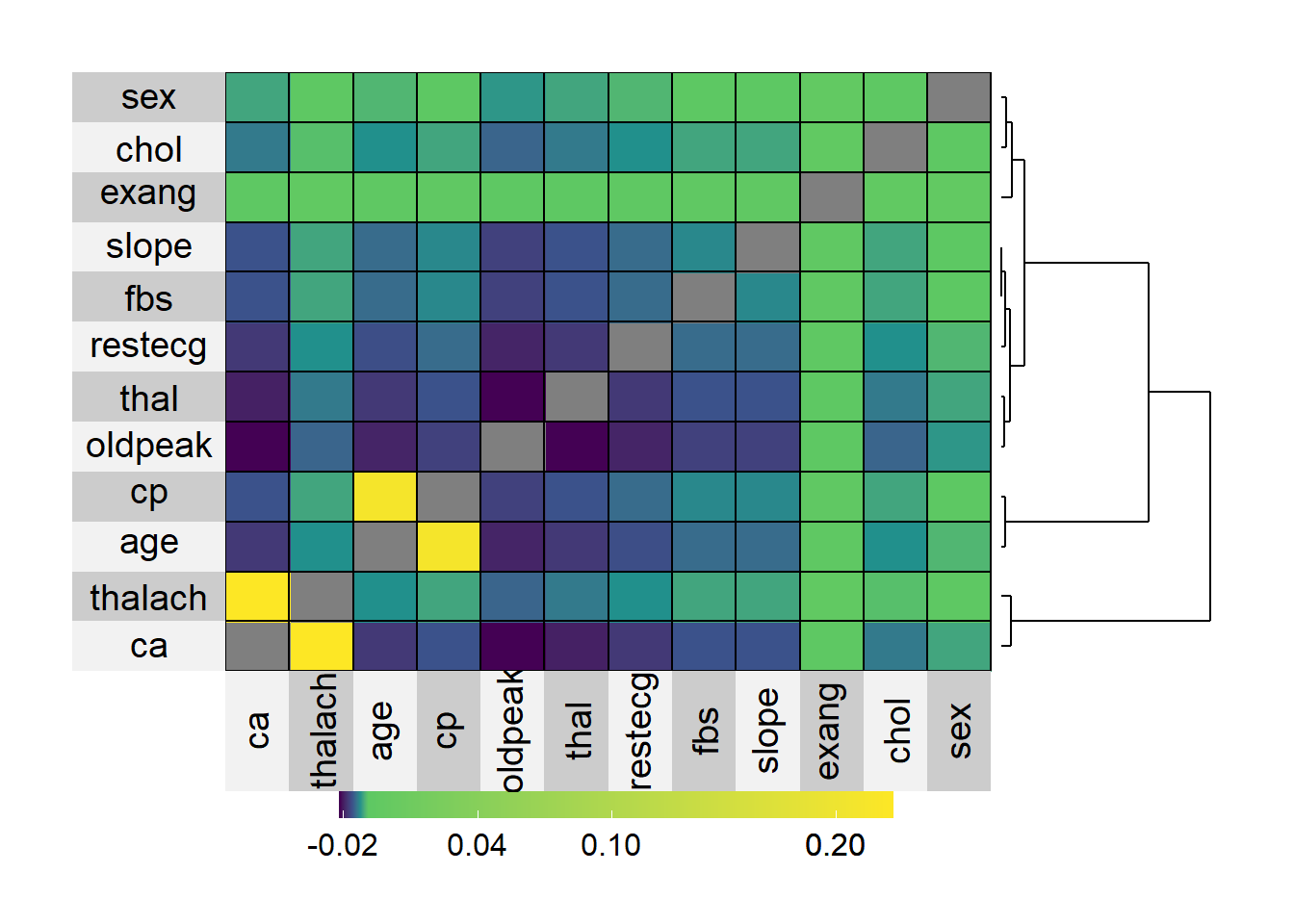
## \end{tabular}3.2.2 Missingness heatmap
if (nrow(missing_df) == 0) {
cat("Skipping missingness heatmap, no missigness found in predictors.")
} else {
# Correlation table of missingness
# Only examine variables with missingness > 0%.
missing2 = is.na(data[, as.character(missing_df$Variable)])
colMeans(missing2)
cor(missing2)
# Correlation matrix of missingness.
(missing_cor = cor(missing2))
# Replace the unit diagonal with NAs so that it doesn't show as yellow.
diag(missing_cor) = NA
# Heatmap of correlation table.
#png("visuals/missingness-superheat.png", height = 600, width = 900)
superheat::superheat(missing_cor,
# Change the angle of the label text
bottom.label.text.angle = 90,
pretty.order.rows = TRUE,
pretty.order.cols = TRUE,
row.dendrogram = TRUE,
scale = FALSE)
#dev.off()
}
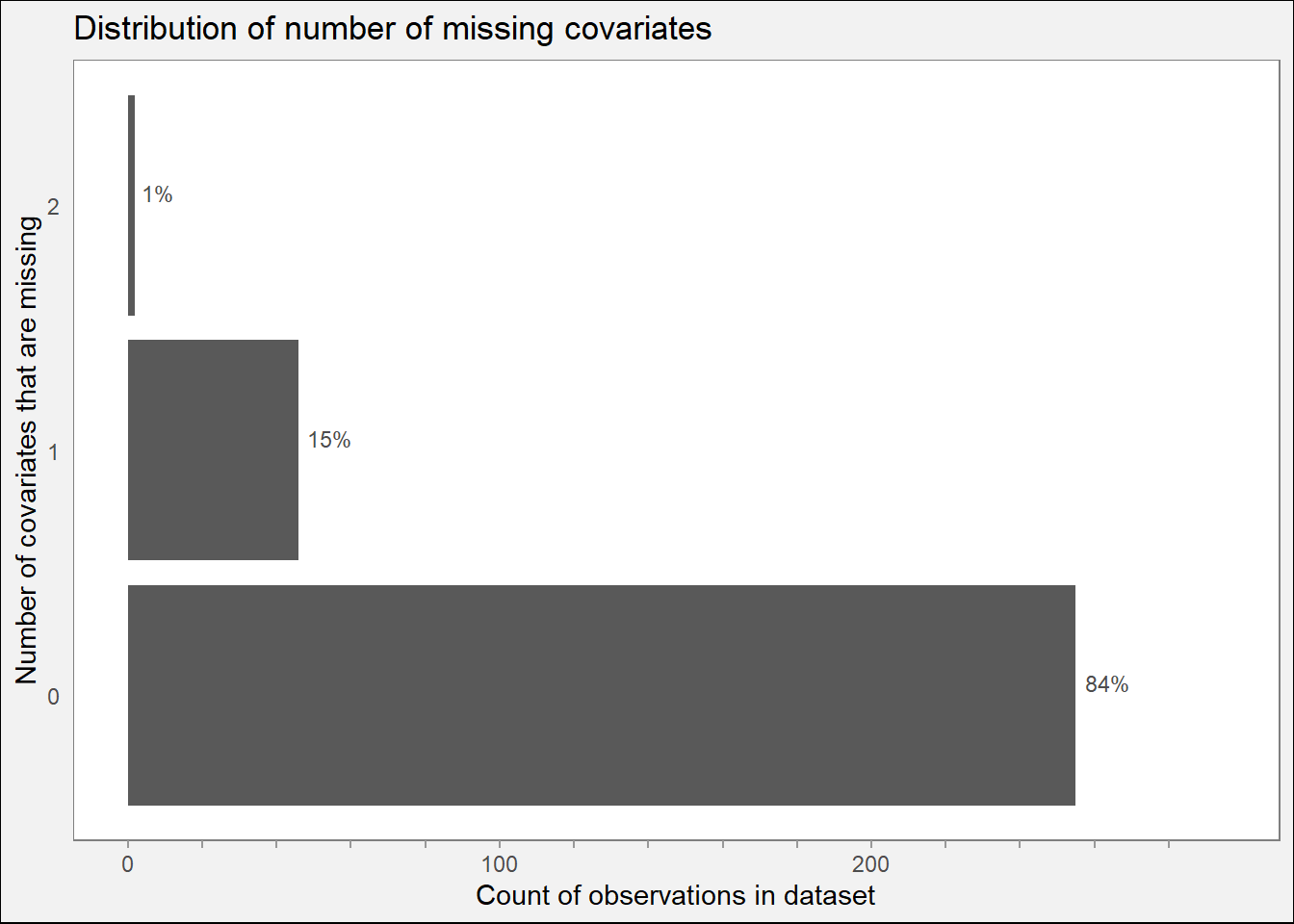
3.2.3 Missingness count plot
if (nrow(missing_df) == 0L) {
cat("Skipping missingness count plot, no missingness found in predictors.")
} else {
# Table with count of missing covariates by observation.
missing_counts = rowSums(missing2)
table(missing_counts)
# Typical observation is missing 6 covariates.
summary(missing_counts)
# Code from:
# https://stackoverflow.com/questions/27850123/ggplot2-have-shorter-tick-marks-for-tick-marks-without-labels?noredirect=1&lq=1
# Major tick marks
major = 100
# Minor tick marks
minor = 20
# Range of x values
# Ensure that we always start at 0.
(range = c(0, 2* minor + sum(missing_counts == as.integer(names(which.max(table(missing_counts)))))))
# Function to insert blank labels
# Borrowed from https://stackoverflow.com/questions/14490071/adding-minor-tick-marks-to-the-x-axis-in-ggplot2-with-no-labels/14490652#14490652
insert_minor <- function(major, n_minor) {
labs <- c(sapply(major, function(x, y) c(x, rep("", y) ), y = round(n_minor)))
labs[1:(length(labs) - n_minor)]
}
# Getting the 'breaks' and 'labels' for the ggplot
n_minor = major / minor - 1
(breaks = seq(min(range), max(range), minor))
(labels = insert_minor(seq(min(range), max(range), major), n_minor))
if (length(breaks) > length(labels)) labels = c(labels, rep("", length(breaks) - length(labels)))
print(ggplot(data.frame(missing_counts), aes(x = missing_counts)) +
geom_bar(aes(y = ..count..)) +
theme_minimal() +
geom_text(aes(label = scales::percent(..prop..), y = ..count..),
stat = "count", hjust = -0.2, size = 3, nudge_x = 0.05,
color = "gray30",
NULL) +
scale_x_continuous(breaks = seq(0, max(table(missing_counts)))) +
scale_y_continuous(breaks = breaks,
labels = ifelse(labels != "", prettyNum(labels, big.mark = ",", preserve.width = "none"), ""),
limits = c(0, max(range))) +
labs(title = "Distribution of number of missing covariates",
x = "Number of covariates that are missing",
y = "Count of observations in dataset") +
# Remove grid axes, add gray background.
# Label each value on x axis.
theme(panel.grid = element_blank(),
axis.ticks.x = element_line(color = "gray60", size = 0.5),
panel.background = element_rect(fill = "white", color = "gray50"),
plot.background = element_rect(fill = "gray95")) +
coord_flip())
ggsave("visuals/missing-count-hist.png", width = 8, height = 4)
# X variables with missingness
print(ncol(missing2))
}
## [1] 123.3 Examine outcome missingness
##
## 0 1
## 138 1653.4 Impute missing predictor values
3.4.1 Missingness indicators
## age sex cp trestbps chol fbs restecg
## 0.01650165 0.00660066 0.01320132 0.00000000 0.00990099 0.01320132 0.01650165
## thalach exang oldpeak slope ca thal
## 0.00990099 0.00330033 0.02310231 0.01320132 0.01980198 0.01980198# First create matrix of missingness indicators for all covariates.
miss_inds =
ck37r::missingness_indicators(data,
skip_vars = c(vars$exclude, vars$outcome),
verbose = TRUE)## Generating 12 missingness indicators.
## Checking for collinearity of indicators.
## Final number of indicators: 12## miss_age miss_sex miss_cp miss_chol miss_fbs miss_restecg
## 0.01650165 0.00660066 0.01320132 0.00990099 0.01320132 0.01650165
## miss_thalach miss_exang miss_oldpeak miss_slope miss_ca miss_thal
## 0.00990099 0.00330033 0.02310231 0.01320132 0.01980198 0.019801983.4.2 Impute to 0
Some variables we want to explicitly set to 0 if they are unobserved.
# Manually impute certain variables to 0 rather than use the sample median (or GLRM).
impute_to_0_vars = c("exang")
# Review missingness one last time for these vars.
colMeans(is.na(data[, impute_to_0_vars, drop = FALSE]))## exang
## 0.00330033## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.0000 0.0000 0.0000 0.3278 1.0000 1.0000 1# Impute these variables specifically to 0, rather than sample median (although
# in many cases the median was already 0).
data[, impute_to_0_vars] = lapply(data[, impute_to_0_vars, drop = FALSE], function(col) {
col[is.na(col)] = 0L
col
})
# Confirm we have no more missingness in these vars.
colMeans(is.na(data[, impute_to_0_vars, drop = FALSE]))## exang
## 0We will use generalized low-rank models in h2o.ai software.
3.4.3 GLRM prep
# Subset using var_df$var so that it's in the same order as var_df.
impute_df = data[, var_df$var]
# Convert binary variables to logical
(binary_vars = var_df$var[var_df$type == "binary"])## character(0)for (binary_name in binary_vars) {
impute_df[[binary_name]] = as.logical(impute_df[[binary_name]])
}
# NOTE: these will be turned into factor variables within h2o.
table(sapply(impute_df, class))##
## factor integer numeric
## 5 7 1# Create a dataframe describing the loss function by variable; the first variable must have index = 0
losses = data.frame("index" = seq(ncol(impute_df)) - 1,
"feature" = var_df$var,
"class" = var_df$class,
"type" = var_df$type,
stringsAsFactors = FALSE)
# Update class for binary variables.
for (binary_name in binary_vars) {
losses[var_df$var == binary_name, "class"] = class(impute_df[[binary_name]])
}
losses$loss[losses$class == "numeric"] = "Huber"
losses$loss[losses$class == "integer"] = "Huber"
#losses$loss[losses$class == "integer"] = "Poisson"
losses$loss[losses$class == "factor"] = "Categorical"
losses$loss[losses$type == "binary"] = "Hinge"
# Logistic seems to yield worse reconstruction RMSE overall.
#losses$loss[losses$type == "binary"] = "Logistic"
losses## index feature class type loss
## 1 0 ca factor categorical Categorical
## 2 1 oldpeak numeric continuous Huber
## 3 2 restecg integer integer Huber
## 4 3 slope factor categorical Categorical
## 5 4 age integer integer Huber
## 6 5 sex factor categorical Categorical
## 7 6 cp factor categorical Categorical
## 8 7 exang integer integer Huber
## 9 8 thal factor categorical Categorical
## 10 9 thalach integer integer Huber
## 11 10 chol integer integer Huber
## 12 11 fbs integer integer Huber
## 13 12 trestbps integer integer Huber3.4.4 Start h2o
# We are avoiding library(h2o) due to namespace conflicts with dplyr & related packages.
# Initialize h2o
h2o::h2o.no_progress() # Turn off progress bars
analyst_name = "chris-kennedy"
h2o::h2o.init(max_mem_size = "15g",
name = paste0("h2o-", analyst_name),
# Default port is 54321, but other analysts may be using that.
port = 54320,
# This can reduce accidental sharing of h2o processes on a shared server.
username = analyst_name,
password = paste0("pw-", analyst_name),
# Use half of available cores for h2o.
nthreads = get_cores())##
## H2O is not running yet, starting it now...
##
## Note: In case of errors look at the following log files:
## C:\Users\chris\AppData\Local\Temp\Rtmpmov5jY\file5fcc2573ccc/h2o_chris_started_from_r.out
## C:\Users\chris\AppData\Local\Temp\Rtmpmov5jY\file5fcc77202047/h2o_chris_started_from_r.err
##
##
## Starting H2O JVM and connecting: Connection successful!
##
## R is connected to the H2O cluster:
## H2O cluster uptime: 3 seconds 750 milliseconds
## H2O cluster timezone: America/Los_Angeles
## H2O data parsing timezone: UTC
## H2O cluster version: 3.30.0.1
## H2O cluster version age: 2 months and 16 days
## H2O cluster name: h2o-chris-kennedy
## H2O cluster total nodes: 1
## H2O cluster total memory: 15.00 GB
## H2O cluster total cores: 12
## H2O cluster allowed cores: 3
## H2O cluster healthy: TRUE
## H2O Connection ip: localhost
## H2O Connection port: 54320
## H2O Connection proxy: NA
## H2O Internal Security: FALSE
## H2O API Extensions: Amazon S3, Algos, AutoML, Core V3, TargetEncoder, Core V4
## R Version: R version 3.6.2 (2019-12-12)3.4.5 Load data into h2o
## Warning in use.package("data.table"): data.table cannot be used without R
## package bit64 version 0.9.7 or higher. Please upgrade to take advangage of
## data.table speedups.## [1] "enum" "real" "int" "enum" "int" "enum" "enum" "int" "enum" "int"
## [11] "int" "int" "int"## index feature class type loss h2o_types
## 1 0 ca factor categorical Categorical enum
## 2 1 oldpeak numeric continuous Huber real
## 3 2 restecg integer integer Huber int
## 4 3 slope factor categorical Categorical enum
## 5 4 age integer integer Huber int
## 6 5 sex factor categorical Categorical enum
## 7 6 cp factor categorical Categorical enum
## 8 7 exang integer integer Huber int
## 9 8 thal factor categorical Categorical enum
## 10 9 thalach integer integer Huber int
## 11 10 chol integer integer Huber int
## 12 11 fbs integer integer Huber int
## 13 12 trestbps integer integer Huber int3.4.6 GLRM train/test split
3.4.7 Define GLRM grid
Follow hyperparameter optimization method shown at: * https://github.com/h2oai/h2o-tutorials/blob/master/best-practices/glrm/GLRM-BestPractices.Rmd * and https://bradleyboehmke.github.io/HOML/GLRM.html#tuning-to-optimize-for-unseen-data
# Create hyperparameter search grid
params = expand.grid(
# Try 3 values on the exponential scale up to the maximum number of predictors.
k = round(exp(log(length(vars$predictors)) * exp(c(-0.8, -0.5, -0.1)))),
regularization_x = c("None", "Quadratic", "L1"),
regularization_y = c("None", "Quadratic", "L1"),
gamma_x = c(0, 1, 4),
gamma_y = c(0, 1, 4),
error_num = NA,
error_cat = NA,
objective = NA,
stringsAsFactors = FALSE)
# 243 combinations!
dim(params)## [1] 243 8# Remove combinations in which regularization_x = None and gamma_x != 0
params = subset(params, regularization_x != "None" | gamma_x == 0)
# Remove combinations in which regularization_x != None and gamma_x == 0
params = subset(params, regularization_x == "None" | gamma_x != 0)
# Remove combinations in which regularization_y = None and gamma_y != 0
params = subset(params, regularization_y != "None" | gamma_y == 0)
# Remove combinations in which regularization_y != None and gamma_y == 0
params = subset(params, regularization_y == "None" | gamma_y != 0)
# Down to 75 combinations.
dim(params)## [1] 75 8## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 1 3 None None 0 0 NA NA
## 2 5 None None 0 0 NA NA
## 3 10 None None 0 0 NA NA
## 31 3 Quadratic None 1 0 NA NA
## 32 5 Quadratic None 1 0 NA NA
## 33 10 Quadratic None 1 0 NA NA
## 34 3 L1 None 1 0 NA NA
## 35 5 L1 None 1 0 NA NA
## 36 10 L1 None 1 0 NA NA
## 58 3 Quadratic None 4 0 NA NA
## 59 5 Quadratic None 4 0 NA NA
## 60 10 Quadratic None 4 0 NA NA
## 61 3 L1 None 4 0 NA NA
## 62 5 L1 None 4 0 NA NA
## 63 10 L1 None 4 0 NA NA
## 91 3 None Quadratic 0 1 NA NA
## 92 5 None Quadratic 0 1 NA NA
## 93 10 None Quadratic 0 1 NA NA
## 100 3 None L1 0 1 NA NA
## 101 5 None L1 0 1 NA NA
## 102 10 None L1 0 1 NA NA
## 121 3 Quadratic Quadratic 1 1 NA NA
## 122 5 Quadratic Quadratic 1 1 NA NA
## 123 10 Quadratic Quadratic 1 1 NA NA
## 124 3 L1 Quadratic 1 1 NA NA
## 125 5 L1 Quadratic 1 1 NA NA
## 126 10 L1 Quadratic 1 1 NA NA
## 130 3 Quadratic L1 1 1 NA NA
## 131 5 Quadratic L1 1 1 NA NA
## 132 10 Quadratic L1 1 1 NA NA
## 133 3 L1 L1 1 1 NA NA
## 134 5 L1 L1 1 1 NA NA
## 135 10 L1 L1 1 1 NA NA
## 148 3 Quadratic Quadratic 4 1 NA NA
## 149 5 Quadratic Quadratic 4 1 NA NA
## 150 10 Quadratic Quadratic 4 1 NA NA
## 151 3 L1 Quadratic 4 1 NA NA
## 152 5 L1 Quadratic 4 1 NA NA
## 153 10 L1 Quadratic 4 1 NA NA
## 157 3 Quadratic L1 4 1 NA NA
## 158 5 Quadratic L1 4 1 NA NA
## 159 10 Quadratic L1 4 1 NA NA
## 160 3 L1 L1 4 1 NA NA
## 161 5 L1 L1 4 1 NA NA
## 162 10 L1 L1 4 1 NA NA
## 172 3 None Quadratic 0 4 NA NA
## 173 5 None Quadratic 0 4 NA NA
## 174 10 None Quadratic 0 4 NA NA
## 181 3 None L1 0 4 NA NA
## 182 5 None L1 0 4 NA NA
## 183 10 None L1 0 4 NA NA
## 202 3 Quadratic Quadratic 1 4 NA NA
## 203 5 Quadratic Quadratic 1 4 NA NA
## 204 10 Quadratic Quadratic 1 4 NA NA
## 205 3 L1 Quadratic 1 4 NA NA
## 206 5 L1 Quadratic 1 4 NA NA
## 207 10 L1 Quadratic 1 4 NA NA
## 211 3 Quadratic L1 1 4 NA NA
## 212 5 Quadratic L1 1 4 NA NA
## 213 10 Quadratic L1 1 4 NA NA
## 214 3 L1 L1 1 4 NA NA
## 215 5 L1 L1 1 4 NA NA
## 216 10 L1 L1 1 4 NA NA
## 229 3 Quadratic Quadratic 4 4 NA NA
## 230 5 Quadratic Quadratic 4 4 NA NA
## 231 10 Quadratic Quadratic 4 4 NA NA
## 232 3 L1 Quadratic 4 4 NA NA
## 233 5 L1 Quadratic 4 4 NA NA
## 234 10 L1 Quadratic 4 4 NA NA
## 238 3 Quadratic L1 4 4 NA NA
## 239 5 Quadratic L1 4 4 NA NA
## 240 10 Quadratic L1 4 4 NA NA
## 241 3 L1 L1 4 4 NA NA
## 242 5 L1 L1 4 4 NA NA
## 243 10 L1 L1 4 4 NA NA
## objective
## 1 NA
## 2 NA
## 3 NA
## 31 NA
## 32 NA
## 33 NA
## 34 NA
## 35 NA
## 36 NA
## 58 NA
## 59 NA
## 60 NA
## 61 NA
## 62 NA
## 63 NA
## 91 NA
## 92 NA
## 93 NA
## 100 NA
## 101 NA
## 102 NA
## 121 NA
## 122 NA
## 123 NA
## 124 NA
## 125 NA
## 126 NA
## 130 NA
## 131 NA
## 132 NA
## 133 NA
## 134 NA
## 135 NA
## 148 NA
## 149 NA
## 150 NA
## 151 NA
## 152 NA
## 153 NA
## 157 NA
## 158 NA
## 159 NA
## 160 NA
## 161 NA
## 162 NA
## 172 NA
## 173 NA
## 174 NA
## 181 NA
## 182 NA
## 183 NA
## 202 NA
## 203 NA
## 204 NA
## 205 NA
## 206 NA
## 207 NA
## 211 NA
## 212 NA
## 213 NA
## 214 NA
## 215 NA
## 216 NA
## 229 NA
## 230 NA
## 231 NA
## 232 NA
## 233 NA
## 234 NA
## 238 NA
## 239 NA
## 240 NA
## 241 NA
## 242 NA
## 243 NA# Randomly order the params so that we can stop at any time.
set.seed(1)
params = params[sample(nrow(params)), ]
params## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 233 5 L1 Quadratic 4 4 NA NA
## 153 10 L1 Quadratic 4 1 NA NA
## 1 3 None None 0 0 NA NA
## 148 3 Quadratic Quadratic 4 1 NA NA
## 160 3 L1 L1 4 1 NA NA
## 62 5 L1 None 4 0 NA NA
## 212 5 Quadratic L1 1 4 NA NA
## 183 10 None L1 0 4 NA NA
## 102 10 None L1 0 1 NA NA
## 204 10 Quadratic Quadratic 1 4 NA NA
## 34 3 L1 None 1 0 NA NA
## 36 10 L1 None 1 0 NA NA
## 63 10 L1 None 4 0 NA NA
## 232 3 L1 Quadratic 4 4 NA NA
## 151 3 L1 Quadratic 4 1 NA NA
## 158 5 Quadratic L1 4 1 NA NA
## 124 3 L1 Quadratic 1 1 NA NA
## 172 3 None Quadratic 0 4 NA NA
## 214 3 L1 L1 1 4 NA NA
## 207 10 L1 Quadratic 1 4 NA NA
## 240 10 Quadratic L1 4 4 NA NA
## 159 10 Quadratic L1 4 1 NA NA
## 234 10 L1 Quadratic 4 4 NA NA
## 161 5 L1 L1 4 1 NA NA
## 216 10 L1 L1 1 4 NA NA
## 135 10 L1 L1 1 1 NA NA
## 101 5 None L1 0 1 NA NA
## 149 5 Quadratic Quadratic 4 1 NA NA
## 33 10 Quadratic None 1 0 NA NA
## 58 3 Quadratic None 4 0 NA NA
## 231 10 Quadratic Quadratic 4 4 NA NA
## 152 5 L1 Quadratic 4 1 NA NA
## 181 3 None L1 0 4 NA NA
## 130 3 Quadratic L1 1 1 NA NA
## 239 5 Quadratic L1 4 4 NA NA
## 122 5 Quadratic Quadratic 1 1 NA NA
## 173 5 None Quadratic 0 4 NA NA
## 203 5 Quadratic Quadratic 1 4 NA NA
## 242 5 L1 L1 4 4 NA NA
## 206 5 L1 Quadratic 1 4 NA NA
## 123 10 Quadratic Quadratic 1 1 NA NA
## 134 5 L1 L1 1 1 NA NA
## 238 3 Quadratic L1 4 4 NA NA
## 2 5 None None 0 0 NA NA
## 61 3 L1 None 4 0 NA NA
## 93 10 None Quadratic 0 1 NA NA
## 121 3 Quadratic Quadratic 1 1 NA NA
## 182 5 None L1 0 4 NA NA
## 150 10 Quadratic Quadratic 4 1 NA NA
## 241 3 L1 L1 4 4 NA NA
## 100 3 None L1 0 1 NA NA
## 202 3 Quadratic Quadratic 1 4 NA NA
## 35 5 L1 None 1 0 NA NA
## 126 10 L1 Quadratic 1 1 NA NA
## 60 10 Quadratic None 4 0 NA NA
## 131 5 Quadratic L1 1 1 NA NA
## 157 3 Quadratic L1 4 1 NA NA
## 230 5 Quadratic Quadratic 4 4 NA NA
## 59 5 Quadratic None 4 0 NA NA
## 125 5 L1 Quadratic 1 1 NA NA
## 31 3 Quadratic None 1 0 NA NA
## 133 3 L1 L1 1 1 NA NA
## 174 10 None Quadratic 0 4 NA NA
## 229 3 Quadratic Quadratic 4 4 NA NA
## 215 5 L1 L1 1 4 NA NA
## 132 10 Quadratic L1 1 1 NA NA
## 243 10 L1 L1 4 4 NA NA
## 211 3 Quadratic L1 1 4 NA NA
## 32 5 Quadratic None 1 0 NA NA
## 162 10 L1 L1 4 1 NA NA
## 92 5 None Quadratic 0 1 NA NA
## 205 3 L1 Quadratic 1 4 NA NA
## 91 3 None Quadratic 0 1 NA NA
## 213 10 Quadratic L1 1 4 NA NA
## 3 10 None None 0 0 NA NA
## objective
## 233 NA
## 153 NA
## 1 NA
## 148 NA
## 160 NA
## 62 NA
## 212 NA
## 183 NA
## 102 NA
## 204 NA
## 34 NA
## 36 NA
## 63 NA
## 232 NA
## 151 NA
## 158 NA
## 124 NA
## 172 NA
## 214 NA
## 207 NA
## 240 NA
## 159 NA
## 234 NA
## 161 NA
## 216 NA
## 135 NA
## 101 NA
## 149 NA
## 33 NA
## 58 NA
## 231 NA
## 152 NA
## 181 NA
## 130 NA
## 239 NA
## 122 NA
## 173 NA
## 203 NA
## 242 NA
## 206 NA
## 123 NA
## 134 NA
## 238 NA
## 2 NA
## 61 NA
## 93 NA
## 121 NA
## 182 NA
## 150 NA
## 241 NA
## 100 NA
## 202 NA
## 35 NA
## 126 NA
## 60 NA
## 131 NA
## 157 NA
## 230 NA
## 59 NA
## 125 NA
## 31 NA
## 133 NA
## 174 NA
## 229 NA
## 215 NA
## 132 NA
## 243 NA
## 211 NA
## 32 NA
## 162 NA
## 92 NA
## 205 NA
## 91 NA
## 213 NA
## 3 NA3.4.8 GLRM grid search
The results of this block are cached because they are slow to compute.
## [1] 75# Perform grid search - takes about 150 seconds.
system.time({
for (i in seq_len(nrow(params))) {
cat("Iteration", i, "of", nrow(params), "", paste0(round(i / nrow(params) * 100, 1), "%\n"))
print(params[i, ])
# Create model
glrm_model = h2o::h2o.glrm(
training_frame = train,
# h2o requires that the validation frame have the same # of rows as the training data for some reason.
#validation_frame = valid,
k = params$k[i],
loss = "Quadratic",
regularization_x = params$regularization_x[i],
regularization_y = params$regularization_y[i],
gamma_x = params$gamma_x[i],
gamma_y = params$gamma_y[i],
transform = "STANDARDIZE",
# This is set artificially low so that it runs quickly during the tutorial.
max_iterations = 30,
# This is a more typical setting:
#max_iterations = 2000,
max_runtime_secs = 1000,
seed = 1,
loss_by_col_idx = losses$index,
loss_by_col = losses$loss)
summ_text = capture.output({ h2o::summary(glrm_model) })
glrm_sum[[i]] = summ_text
h2o::summary(glrm_model)
plot(glrm_model)
params$objective[i] = glrm_model@model$objective
# Predict on validation set and extract error
# Warning: this can throw java.lang.ArrayIndexOutOfBoundsException
try({
validate = h2o::h2o.performance(glrm_model, valid)
#print(validate@metrics)
glrm_metrics[[i]] = validate@metrics
params$error_num[i] = validate@metrics$numerr
params$error_cat[i] = validate@metrics$caterr
})
# Removing the model prevents the index error from occurring!
h2o::h2o.rm(glrm_model)
# Save after each iteration in case it crashes.
# This could go inside the try()
# params should be the first object.
save(params, glrm_metrics, glrm_sum,
file = "data/glrm-tuned-results.RData")
}
})## Iteration 1 of 75 1.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 233 5 L1 Quadratic 4 4 NA NA
## objective
## 233 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_1
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 3078.15172
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1548.359
## Misclassification Error (Categorical): 330
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:07 0.257 sec 0 1.05000 4771.95362
## 2 2020-06-20 06:42:07 0.272 sec 1 1.10250 4264.58709
## 3 2020-06-20 06:42:07 0.280 sec 2 0.73500 4264.58709
## 4 2020-06-20 06:42:07 0.288 sec 3 0.49000 4264.58709
## 5 2020-06-20 06:42:07 0.300 sec 4 0.51450 4002.73529
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:07 0.428 sec 24 0.05678 3101.76007
## 26 2020-06-20 06:42:07 0.434 sec 25 0.05962 3089.45461
## 27 2020-06-20 06:42:07 0.437 sec 26 0.06260 3088.97874
## 28 2020-06-20 06:42:07 0.441 sec 27 0.06573 3087.10244
## 29 2020-06-20 06:42:07 0.445 sec 28 0.04382 3087.10244
## 30 2020-06-20 06:42:07 0.450 sec 29 0.04601 3078.15172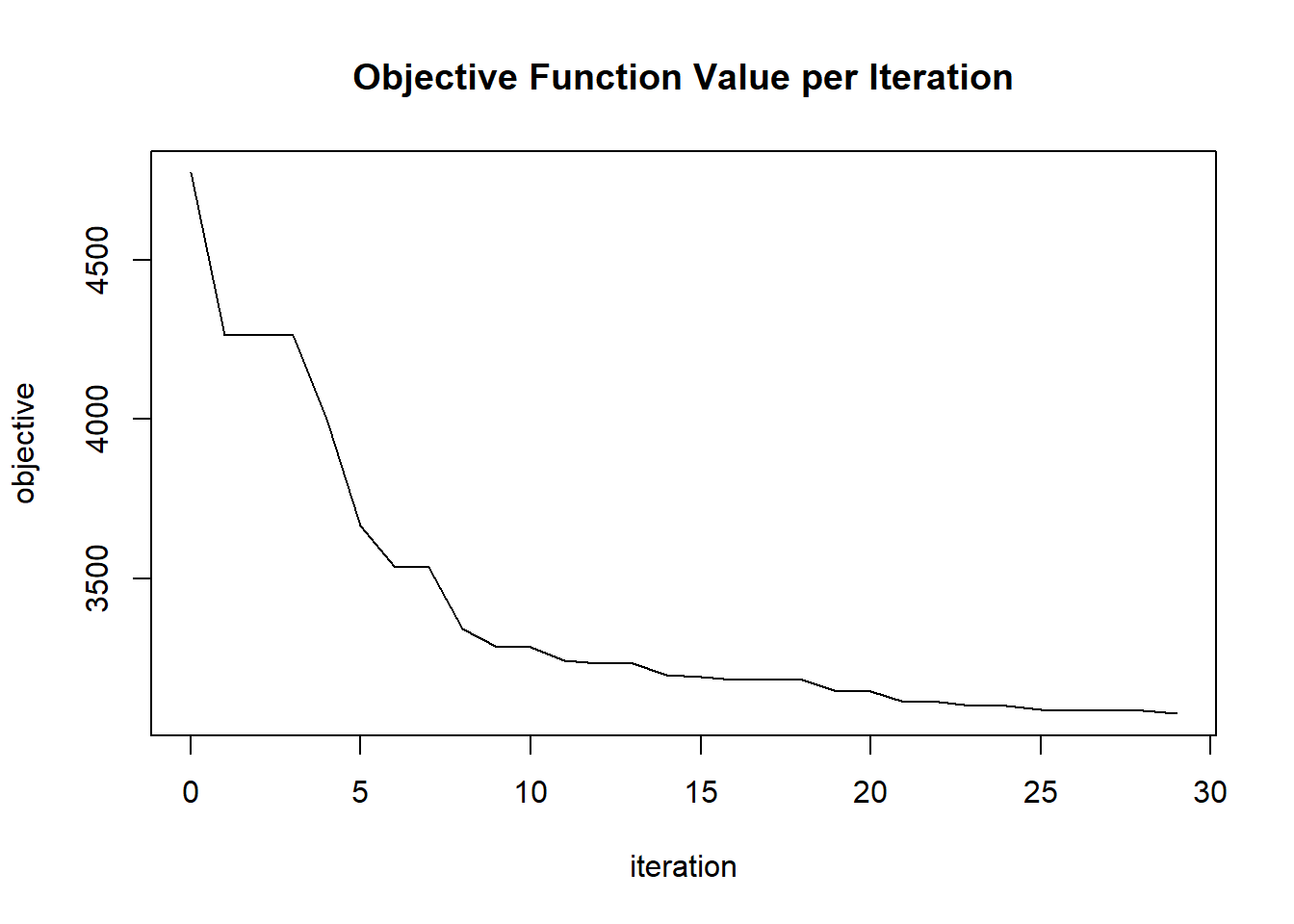
## Iteration 2 of 75 2.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 153 10 L1 Quadratic 4 1 NA NA
## objective
## 153 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_3
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 2517.74751
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1340.119
## Misclassification Error (Categorical): 173
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:08 0.038 sec 0 1.05000 4502.23608
## 2 2020-06-20 06:42:08 0.042 sec 1 0.70000 4502.23608
## 3 2020-06-20 06:42:08 0.047 sec 2 0.73500 3788.22992
## 4 2020-06-20 06:42:08 0.053 sec 3 0.49000 3788.22992
## 5 2020-06-20 06:42:08 0.058 sec 4 0.51450 3551.78004
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:09 0.179 sec 24 0.14085 2563.08937
## 26 2020-06-20 06:42:09 0.187 sec 25 0.09390 2563.08937
## 27 2020-06-20 06:42:09 0.192 sec 26 0.09860 2543.64513
## 28 2020-06-20 06:42:09 0.197 sec 27 0.10353 2531.74728
## 29 2020-06-20 06:42:09 0.202 sec 28 0.06902 2531.74728
## 30 2020-06-20 06:42:09 0.206 sec 29 0.07247 2517.74751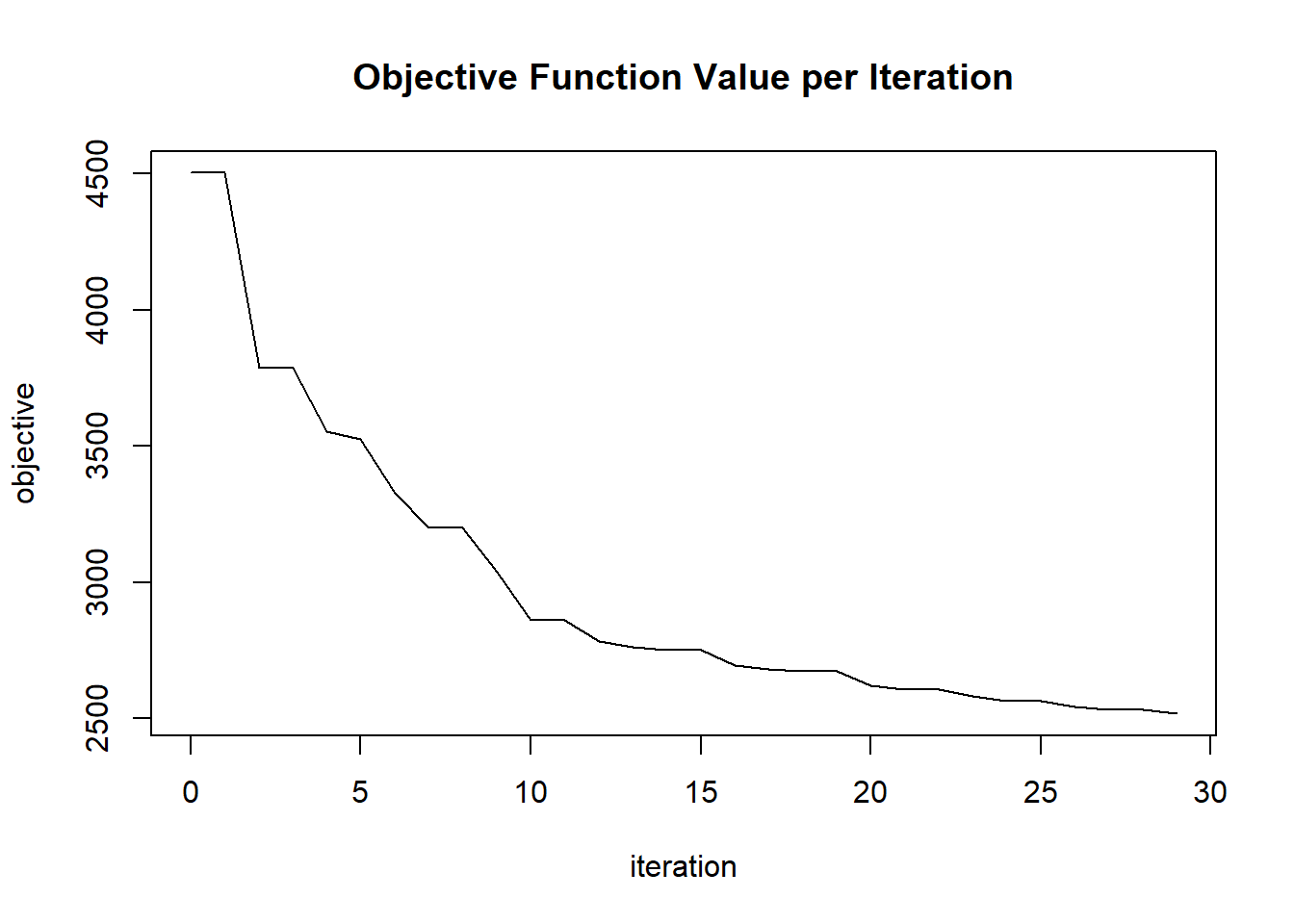
## Iteration 3 of 75 4%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 1 3 None None 0 0 NA NA
## objective
## 1 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_5
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.03451 1903.07151
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1298.219
## Misclassification Error (Categorical): 325
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:10 0.026 sec 0 1.05000 2446.80542
## 2 2020-06-20 06:42:10 0.033 sec 1 0.70000 2446.80542
## 3 2020-06-20 06:42:10 0.038 sec 2 0.46667 2446.80542
## 4 2020-06-20 06:42:10 0.046 sec 3 0.31111 2446.80542
## 5 2020-06-20 06:42:10 0.053 sec 4 0.15556 2446.80542
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:10 0.162 sec 24 0.04259 1911.14025
## 26 2020-06-20 06:42:10 0.166 sec 25 0.04472 1910.48527
## 27 2020-06-20 06:42:10 0.171 sec 26 0.04695 1908.46755
## 28 2020-06-20 06:42:10 0.176 sec 27 0.04930 1905.78622
## 29 2020-06-20 06:42:10 0.183 sec 28 0.03287 1905.78622
## 30 2020-06-20 06:42:10 0.187 sec 29 0.03451 1903.07151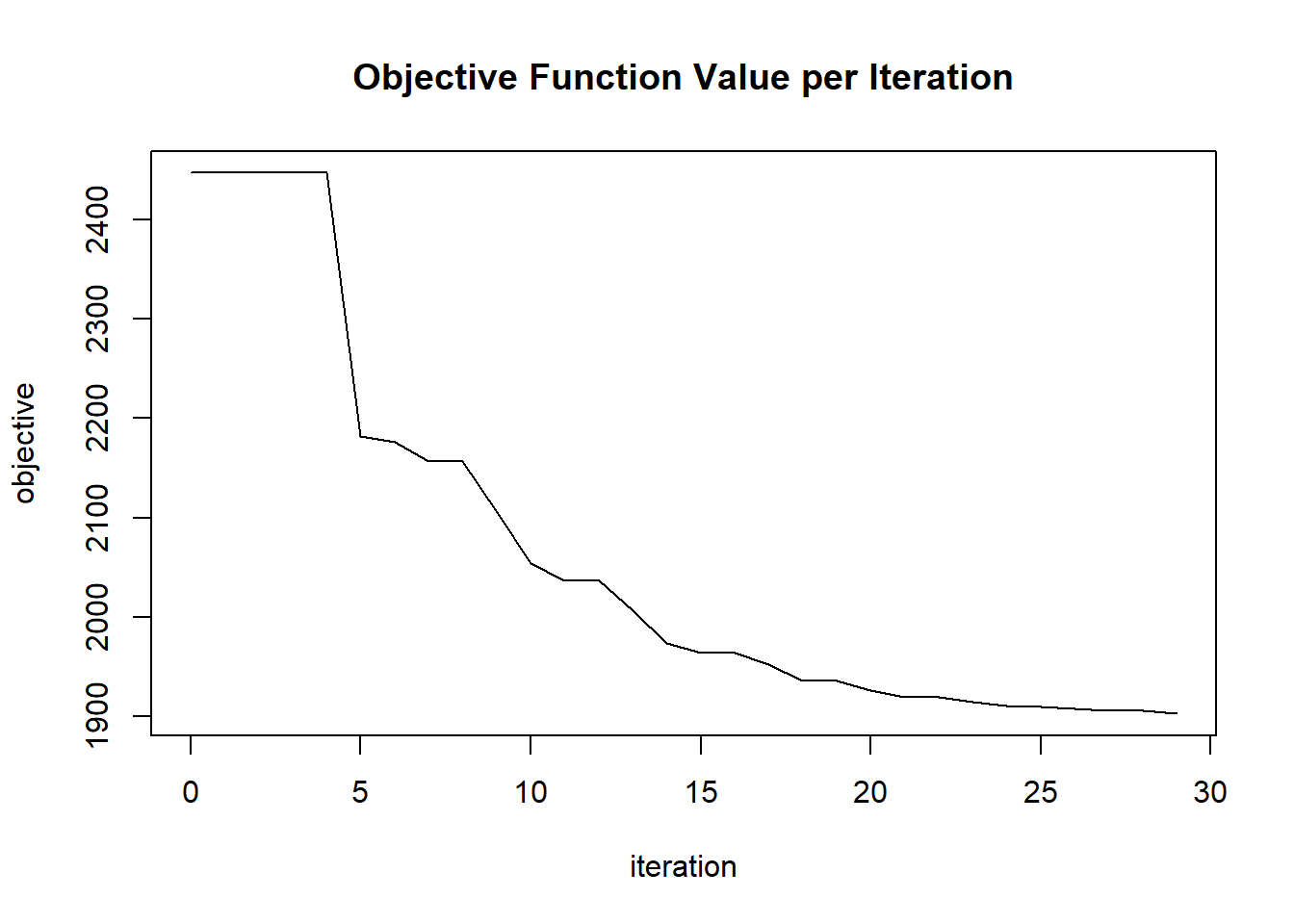
## Iteration 4 of 75 5.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 148 3 Quadratic Quadratic 4 1 NA NA
## objective
## 148 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_7
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.02921 2405.49655
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1358.582
## Misclassification Error (Categorical): 355
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:12 0.026 sec 0 1.05000 2871.85433
## 2 2020-06-20 06:42:12 0.032 sec 1 0.70000 2871.85433
## 3 2020-06-20 06:42:12 0.039 sec 2 0.46667 2871.85433
## 4 2020-06-20 06:42:12 0.044 sec 3 0.31111 2871.85433
## 5 2020-06-20 06:42:12 0.049 sec 4 0.32667 2822.44503
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:12 0.150 sec 24 0.05678 2415.05649
## 26 2020-06-20 06:42:12 0.154 sec 25 0.03785 2415.05649
## 27 2020-06-20 06:42:12 0.160 sec 26 0.03975 2410.09312
## 28 2020-06-20 06:42:12 0.164 sec 27 0.04173 2408.33081
## 29 2020-06-20 06:42:12 0.167 sec 28 0.02782 2408.33081
## 30 2020-06-20 06:42:12 0.169 sec 29 0.02921 2405.49655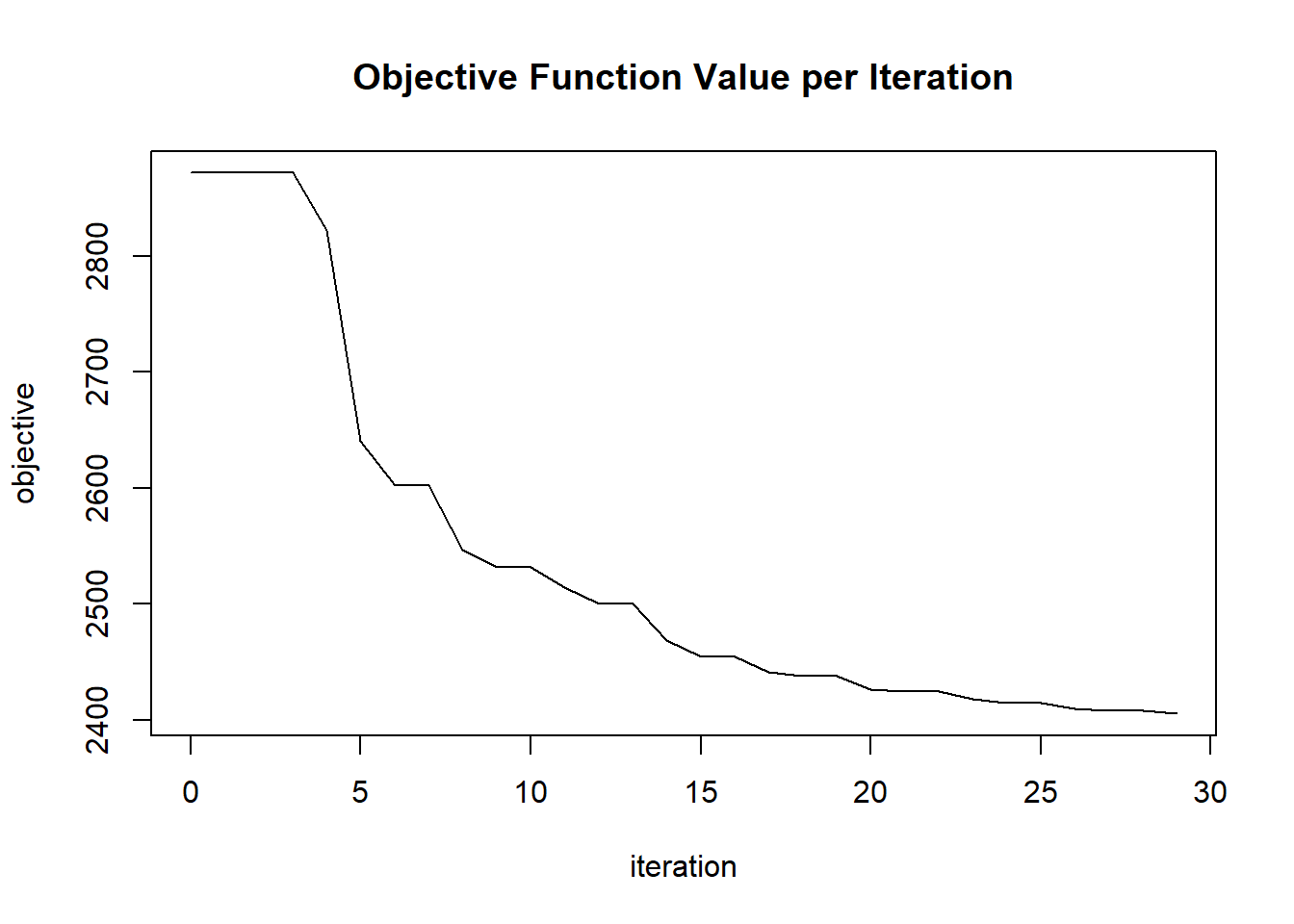
## Iteration 5 of 75 6.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 160 3 L1 L1 4 1 NA NA
## objective
## 160 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_9
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 2572.00653
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1452.309
## Misclassification Error (Categorical): 360
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:13 0.025 sec 0 1.05000 4147.94914
## 2 2020-06-20 06:42:13 0.027 sec 1 0.70000 4147.94914
## 3 2020-06-20 06:42:13 0.029 sec 2 0.46667 4147.94914
## 4 2020-06-20 06:42:13 0.031 sec 3 0.49000 3201.29998
## 5 2020-06-20 06:42:13 0.033 sec 4 0.51450 3066.89359
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:13 0.081 sec 24 0.05678 2599.59738
## 26 2020-06-20 06:42:13 0.084 sec 25 0.05962 2590.97615
## 27 2020-06-20 06:42:13 0.085 sec 26 0.06260 2582.01057
## 28 2020-06-20 06:42:13 0.087 sec 27 0.04173 2582.01057
## 29 2020-06-20 06:42:13 0.089 sec 28 0.04382 2575.75859
## 30 2020-06-20 06:42:13 0.090 sec 29 0.04601 2572.00653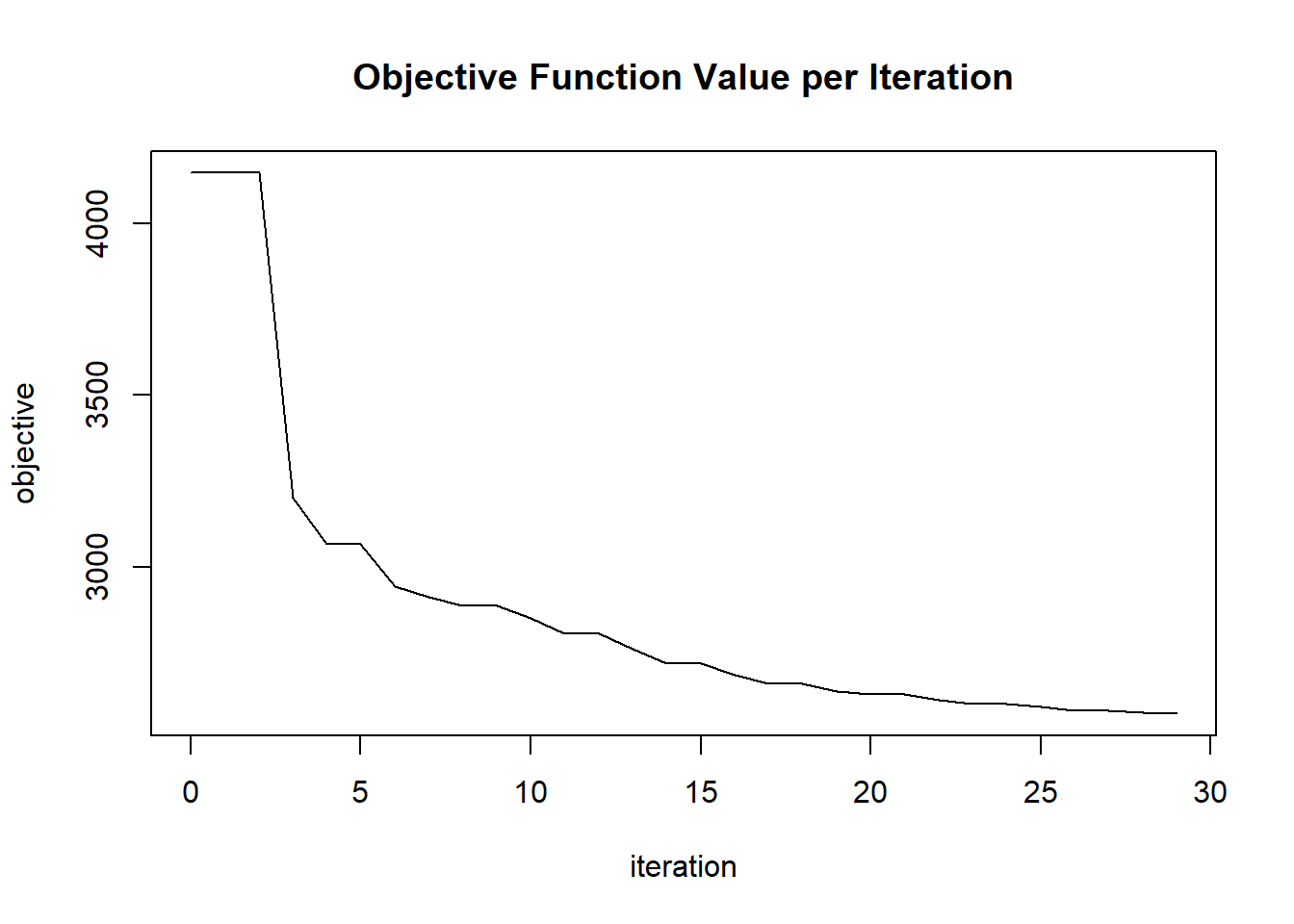
## Iteration 6 of 75 8%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 62 5 L1 None 4 0 NA NA
## objective
## 62 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_11
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 2170.55916
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1366.474
## Misclassification Error (Categorical): 243
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:15 0.056 sec 0 1.05000 4299.99970
## 2 2020-06-20 06:42:15 0.060 sec 1 0.70000 4299.99970
## 3 2020-06-20 06:42:15 0.063 sec 2 0.73500 4051.36990
## 4 2020-06-20 06:42:15 0.066 sec 3 0.77175 3736.02992
## 5 2020-06-20 06:42:15 0.068 sec 4 0.51450 3736.02992
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:15 0.119 sec 24 0.05678 2214.74930
## 26 2020-06-20 06:42:15 0.122 sec 25 0.05962 2200.28783
## 27 2020-06-20 06:42:15 0.124 sec 26 0.06260 2190.57979
## 28 2020-06-20 06:42:15 0.127 sec 27 0.04173 2190.57979
## 29 2020-06-20 06:42:15 0.130 sec 28 0.04382 2177.78252
## 30 2020-06-20 06:42:15 0.132 sec 29 0.04601 2170.55916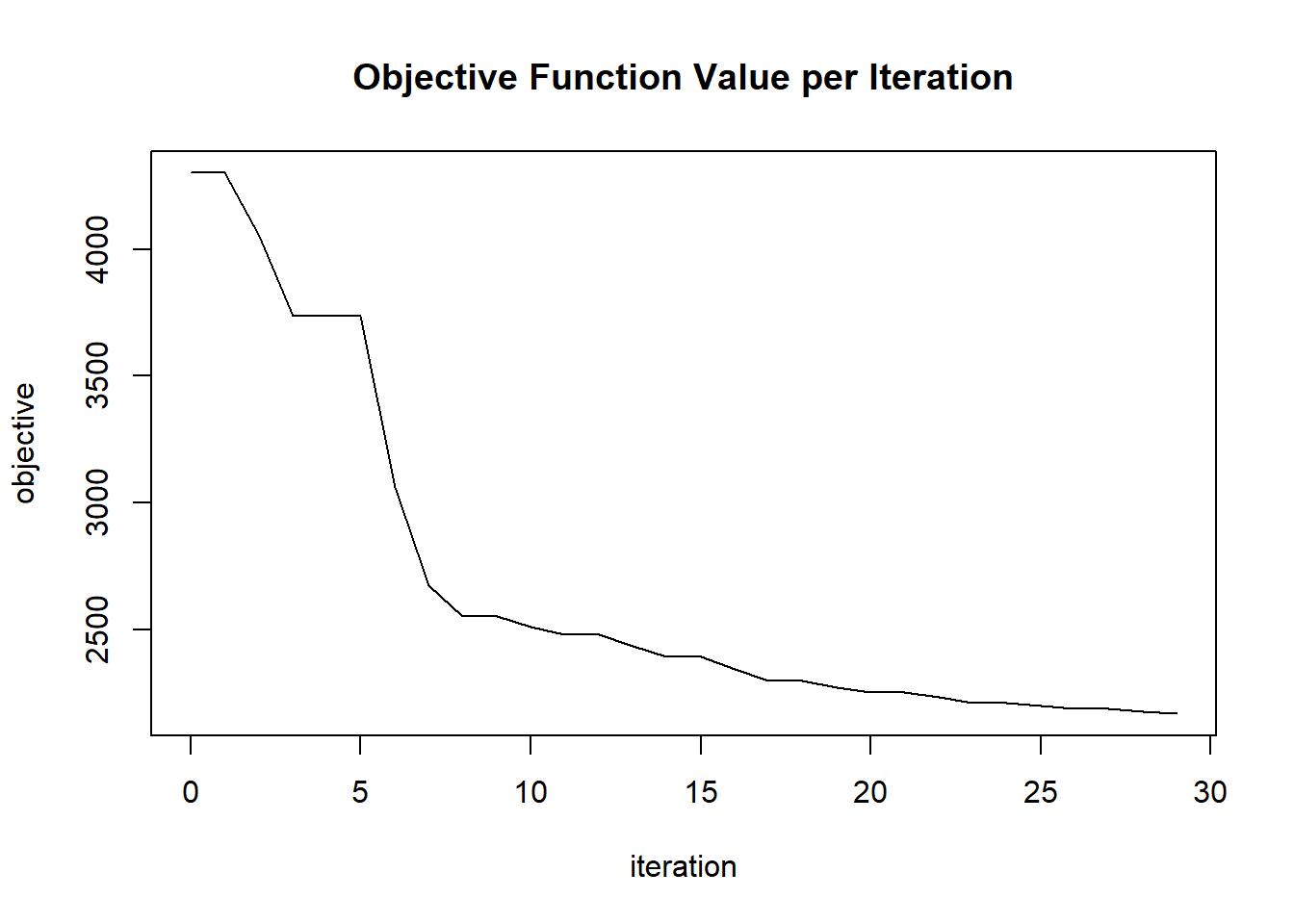
## Iteration 7 of 75 9.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 212 5 Quadratic L1 1 4 NA NA
## objective
## 212 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_13
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 1737.18758
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1439.787
## Misclassification Error (Categorical): 126
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:17 0.049 sec 0 1.05000 2940.72016
## 2 2020-06-20 06:42:17 0.053 sec 1 0.70000 2940.72016
## 3 2020-06-20 06:42:17 0.056 sec 2 0.46667 2940.72016
## 4 2020-06-20 06:42:17 0.059 sec 3 0.31111 2940.72016
## 5 2020-06-20 06:42:17 0.064 sec 4 0.32667 2817.45159
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:17 0.117 sec 24 0.22184 1768.41663
## 26 2020-06-20 06:42:17 0.119 sec 25 0.23294 1765.68228
## 27 2020-06-20 06:42:17 0.122 sec 26 0.24458 1765.04244
## 28 2020-06-20 06:42:17 0.125 sec 27 0.25681 1763.97881
## 29 2020-06-20 06:42:17 0.129 sec 28 0.17121 1763.97881
## 30 2020-06-20 06:42:17 0.132 sec 29 0.17977 1737.18758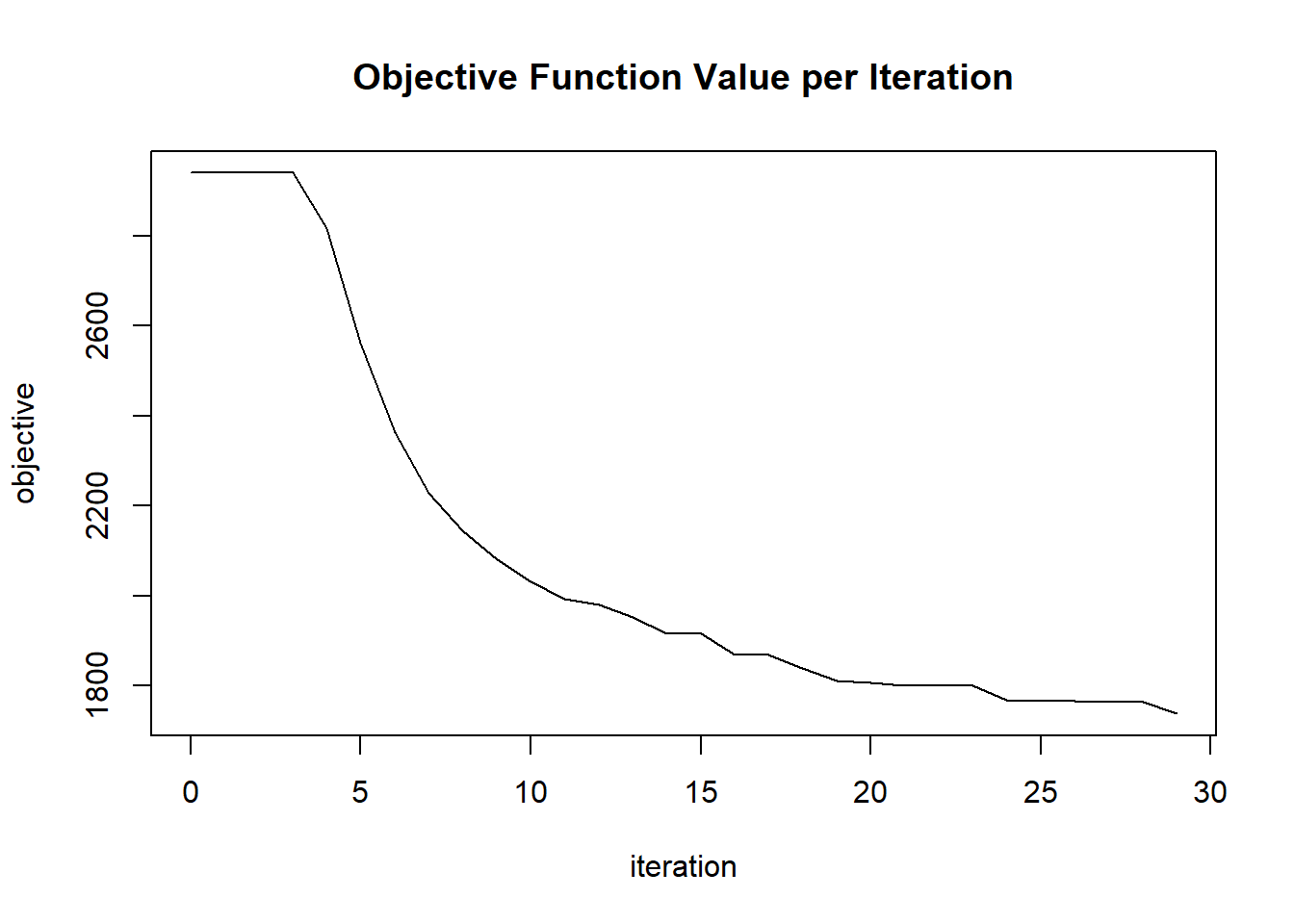
## Iteration 8 of 75 10.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 183 10 None L1 0 4 NA NA
## objective
## 183 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_15
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 970.47294
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 761.7432
## Misclassification Error (Categorical): 55
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:18 0.035 sec 0 1.05000 4057.18290
## 2 2020-06-20 06:42:18 0.040 sec 1 0.70000 4057.18290
## 3 2020-06-20 06:42:18 0.046 sec 2 0.46667 4057.18290
## 4 2020-06-20 06:42:18 0.050 sec 3 0.49000 3545.77830
## 5 2020-06-20 06:42:18 0.053 sec 4 0.51450 3118.80625
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:18 0.164 sec 24 0.22184 1028.03950
## 26 2020-06-20 06:42:18 0.167 sec 25 0.23294 1016.89414
## 27 2020-06-20 06:42:18 0.172 sec 26 0.24458 1011.43623
## 28 2020-06-20 06:42:18 0.179 sec 27 0.16306 1011.43623
## 29 2020-06-20 06:42:18 0.184 sec 28 0.17121 983.41864
## 30 2020-06-20 06:42:18 0.189 sec 29 0.17977 970.47294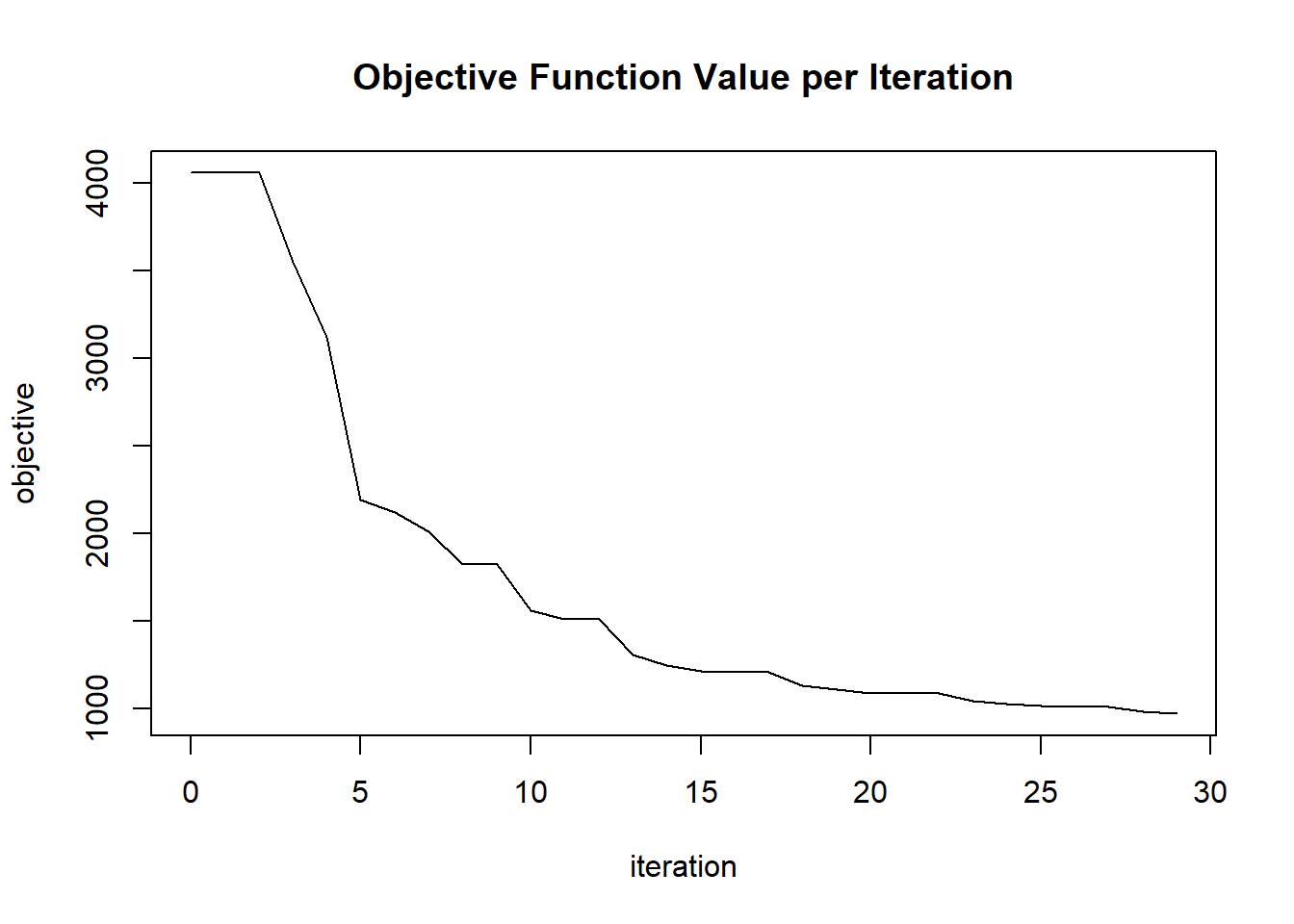
## Iteration 9 of 75 12%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 102 10 None L1 0 1 NA NA
## objective
## 102 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_17
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.28314 647.60549
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 551.2013
## Misclassification Error (Categorical): 25
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:20 0.027 sec 0 1.05000 3568.49501
## 2 2020-06-20 06:42:20 0.031 sec 1 0.70000 3568.49501
## 3 2020-06-20 06:42:20 0.034 sec 2 0.46667 3568.49501
## 4 2020-06-20 06:42:20 0.037 sec 3 0.31111 3568.49501
## 5 2020-06-20 06:42:20 0.041 sec 4 0.32667 2320.28803
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:20 0.110 sec 24 0.34941 703.21917
## 26 2020-06-20 06:42:20 0.113 sec 25 0.23294 703.21917
## 27 2020-06-20 06:42:20 0.117 sec 26 0.24458 673.13521
## 28 2020-06-20 06:42:20 0.120 sec 27 0.25681 660.26034
## 29 2020-06-20 06:42:20 0.124 sec 28 0.26965 650.69811
## 30 2020-06-20 06:42:20 0.127 sec 29 0.28314 647.60549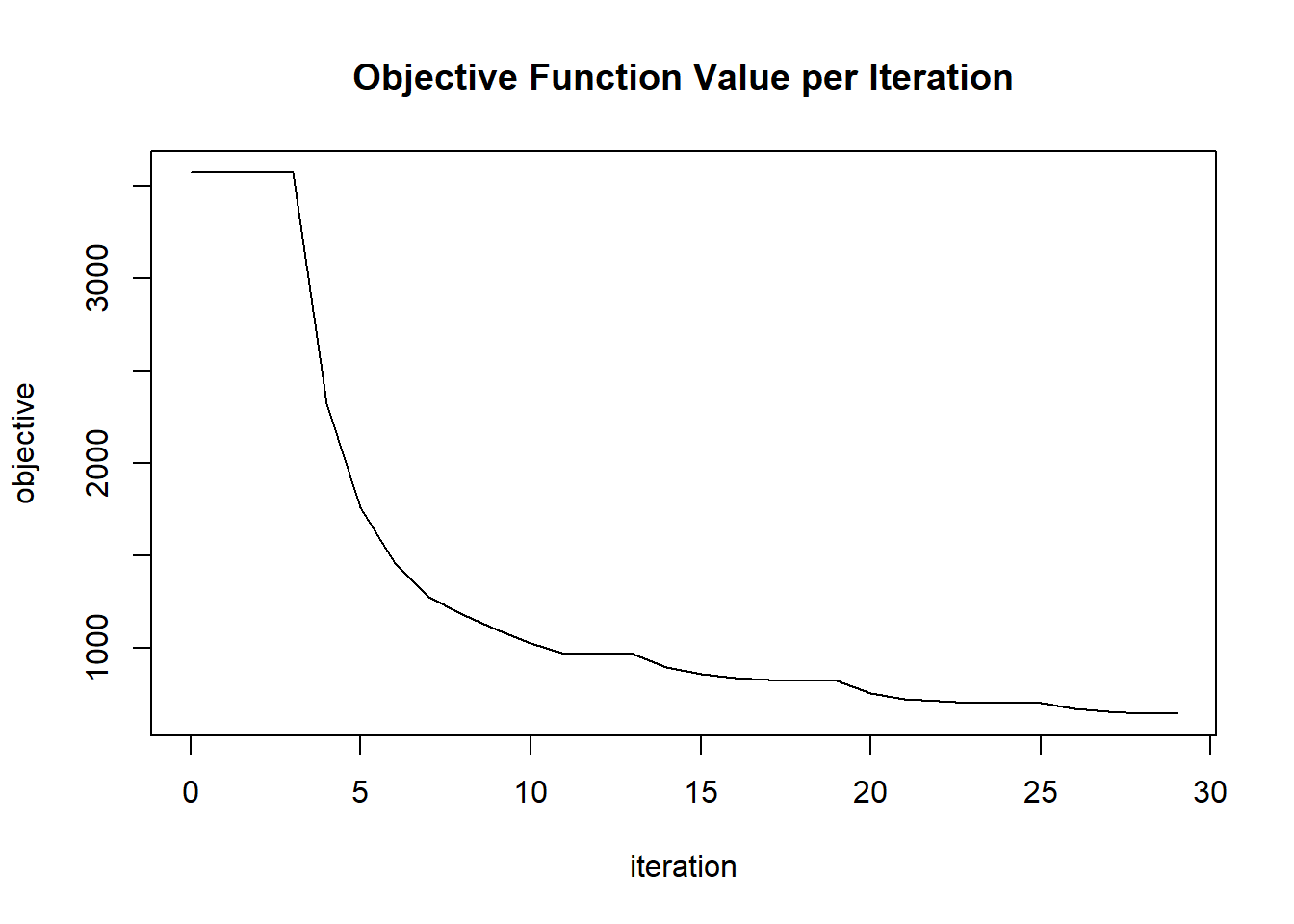
## Iteration 10 of 75 13.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 204 10 Quadratic Quadratic 1 4 NA NA
## objective
## 204 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_19
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 1608.29066
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 886.3189
## Misclassification Error (Categorical): 97
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:22 0.035 sec 0 1.05000 3495.23576
## 2 2020-06-20 06:42:22 0.039 sec 1 0.70000 3495.23576
## 3 2020-06-20 06:42:22 0.043 sec 2 0.46667 3495.23576
## 4 2020-06-20 06:42:22 0.048 sec 3 0.49000 2652.37360
## 5 2020-06-20 06:42:22 0.051 sec 4 0.51450 2480.93892
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:22 0.126 sec 24 0.14085 1634.53029
## 26 2020-06-20 06:42:22 0.131 sec 25 0.09390 1634.53029
## 27 2020-06-20 06:42:22 0.135 sec 26 0.09860 1618.58550
## 28 2020-06-20 06:42:22 0.139 sec 27 0.10353 1618.39309
## 29 2020-06-20 06:42:22 0.144 sec 28 0.06902 1618.39309
## 30 2020-06-20 06:42:22 0.149 sec 29 0.07247 1608.29066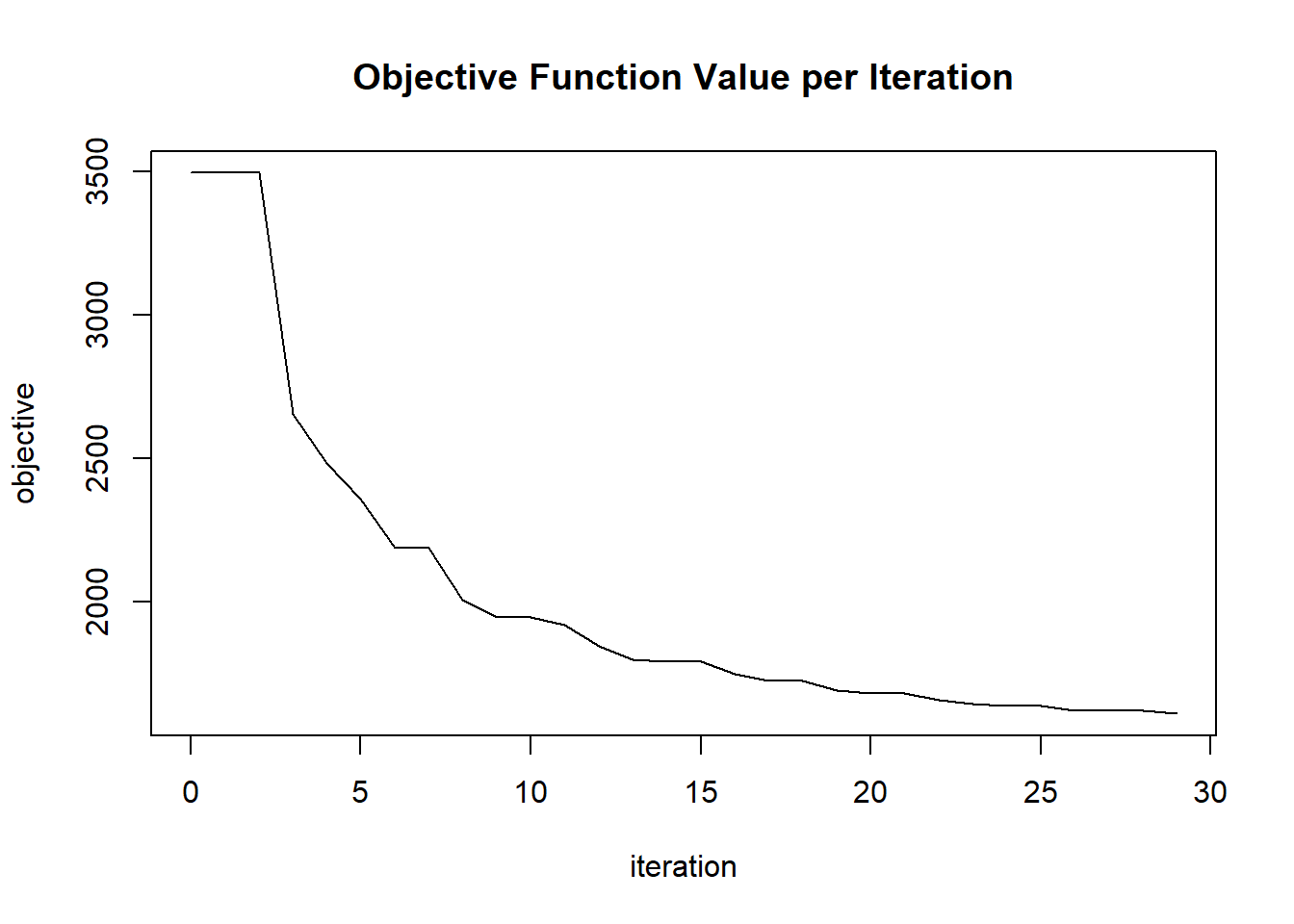
## Iteration 11 of 75 14.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 34 3 L1 None 1 0 NA NA
## objective
## 34 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_21
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.03451 2077.69944
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1326.069
## Misclassification Error (Categorical): 357
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:23 0.016 sec 0 1.05000 2393.57535
## 2 2020-06-20 06:42:23 0.018 sec 1 0.70000 2393.57535
## 3 2020-06-20 06:42:23 0.019 sec 2 0.46667 2393.57535
## 4 2020-06-20 06:42:23 0.021 sec 3 0.31111 2393.57535
## 5 2020-06-20 06:42:23 0.023 sec 4 0.15556 2393.57535
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:23 0.056 sec 24 0.04259 2085.11774
## 26 2020-06-20 06:42:23 0.057 sec 25 0.04472 2084.85913
## 27 2020-06-20 06:42:23 0.059 sec 26 0.02981 2084.85913
## 28 2020-06-20 06:42:23 0.061 sec 27 0.03130 2080.09261
## 29 2020-06-20 06:42:23 0.062 sec 28 0.03287 2077.80021
## 30 2020-06-20 06:42:23 0.063 sec 29 0.03451 2077.69944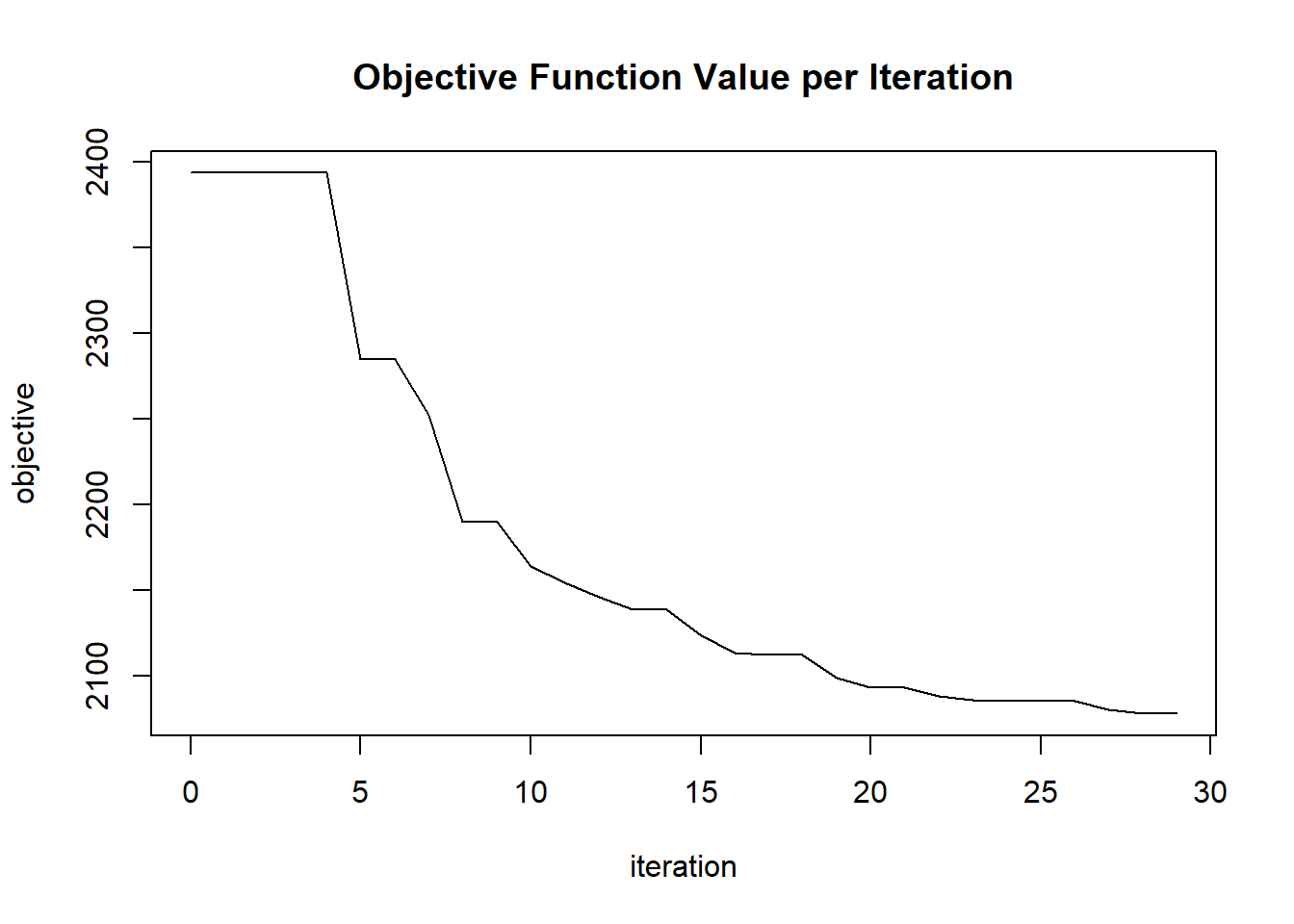
## Iteration 12 of 75 16%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 36 10 L1 None 1 0 NA NA
## objective
## 36 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_23
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.11414 993.93860
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 585.2555
## Misclassification Error (Categorical): 52
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:25 0.035 sec 0 1.05000 2835.49005
## 2 2020-06-20 06:42:25 0.039 sec 1 0.70000 2835.49005
## 3 2020-06-20 06:42:25 0.047 sec 2 0.46667 2835.49005
## 4 2020-06-20 06:42:25 0.052 sec 3 0.31111 2835.49005
## 5 2020-06-20 06:42:25 0.055 sec 4 0.32667 2247.03667
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:25 0.146 sec 24 0.22184 1043.90853
## 26 2020-06-20 06:42:25 0.151 sec 25 0.14790 1043.90853
## 27 2020-06-20 06:42:25 0.155 sec 26 0.15529 1019.55837
## 28 2020-06-20 06:42:25 0.159 sec 27 0.16306 1012.07422
## 29 2020-06-20 06:42:25 0.164 sec 28 0.10870 1012.07422
## 30 2020-06-20 06:42:25 0.167 sec 29 0.11414 993.93860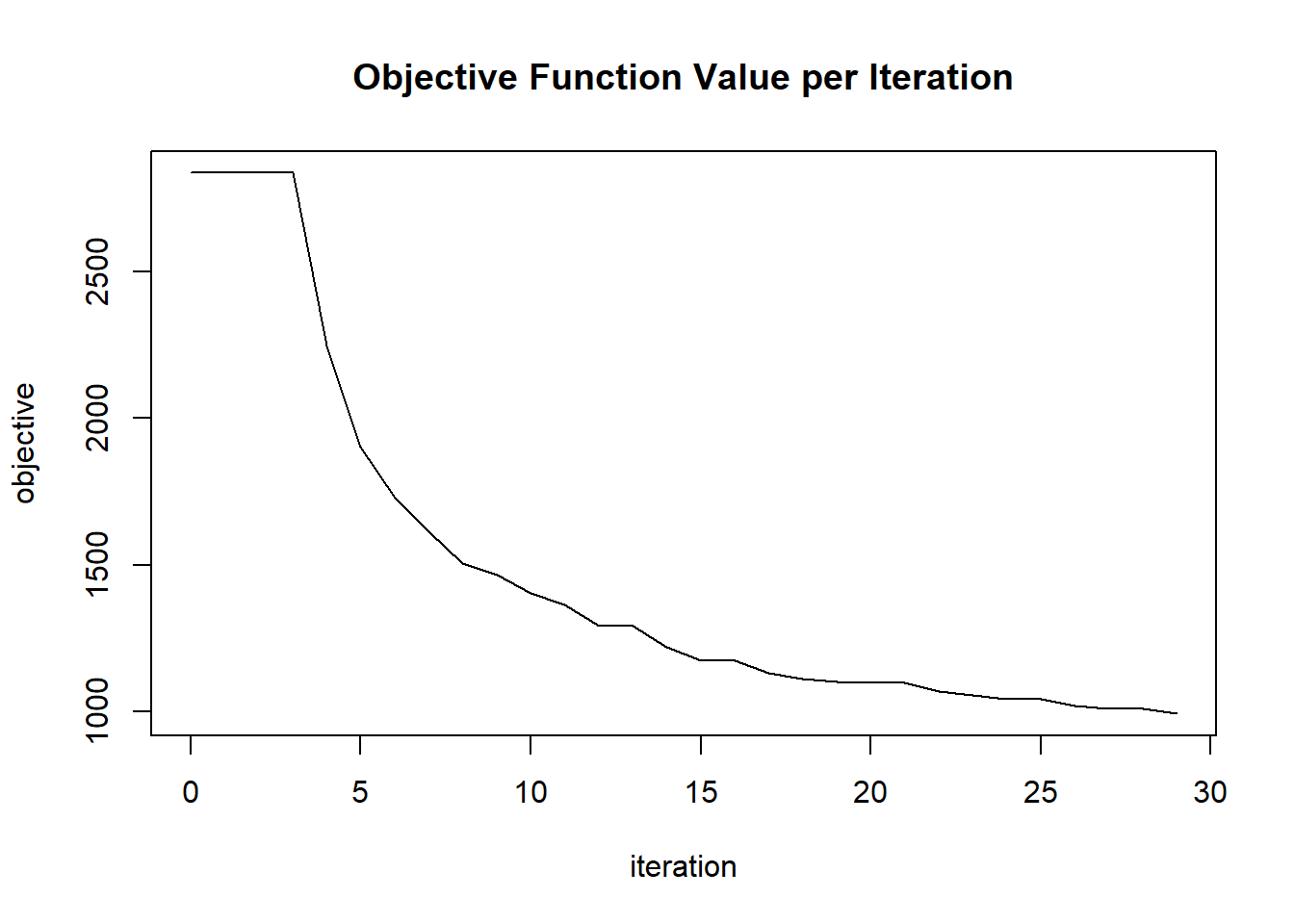
## Iteration 13 of 75 17.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 63 10 L1 None 4 0 NA NA
## objective
## 63 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_25
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 1959.41313
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1108.732
## Misclassification Error (Categorical): 140
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:26 0.025 sec 0 1.05000 4240.23364
## 2 2020-06-20 06:42:26 0.028 sec 1 0.70000 4240.23364
## 3 2020-06-20 06:42:26 0.031 sec 2 0.73500 3769.95950
## 4 2020-06-20 06:42:26 0.035 sec 3 0.49000 3769.95950
## 5 2020-06-20 06:42:26 0.038 sec 4 0.51450 3278.63616
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:26 0.104 sec 24 0.08943 2023.27074
## 26 2020-06-20 06:42:26 0.106 sec 25 0.09390 1999.13999
## 27 2020-06-20 06:42:26 0.109 sec 26 0.06260 1999.13999
## 28 2020-06-20 06:42:26 0.113 sec 27 0.06573 1975.68901
## 29 2020-06-20 06:42:26 0.117 sec 28 0.06902 1960.73931
## 30 2020-06-20 06:42:26 0.121 sec 29 0.07247 1959.41313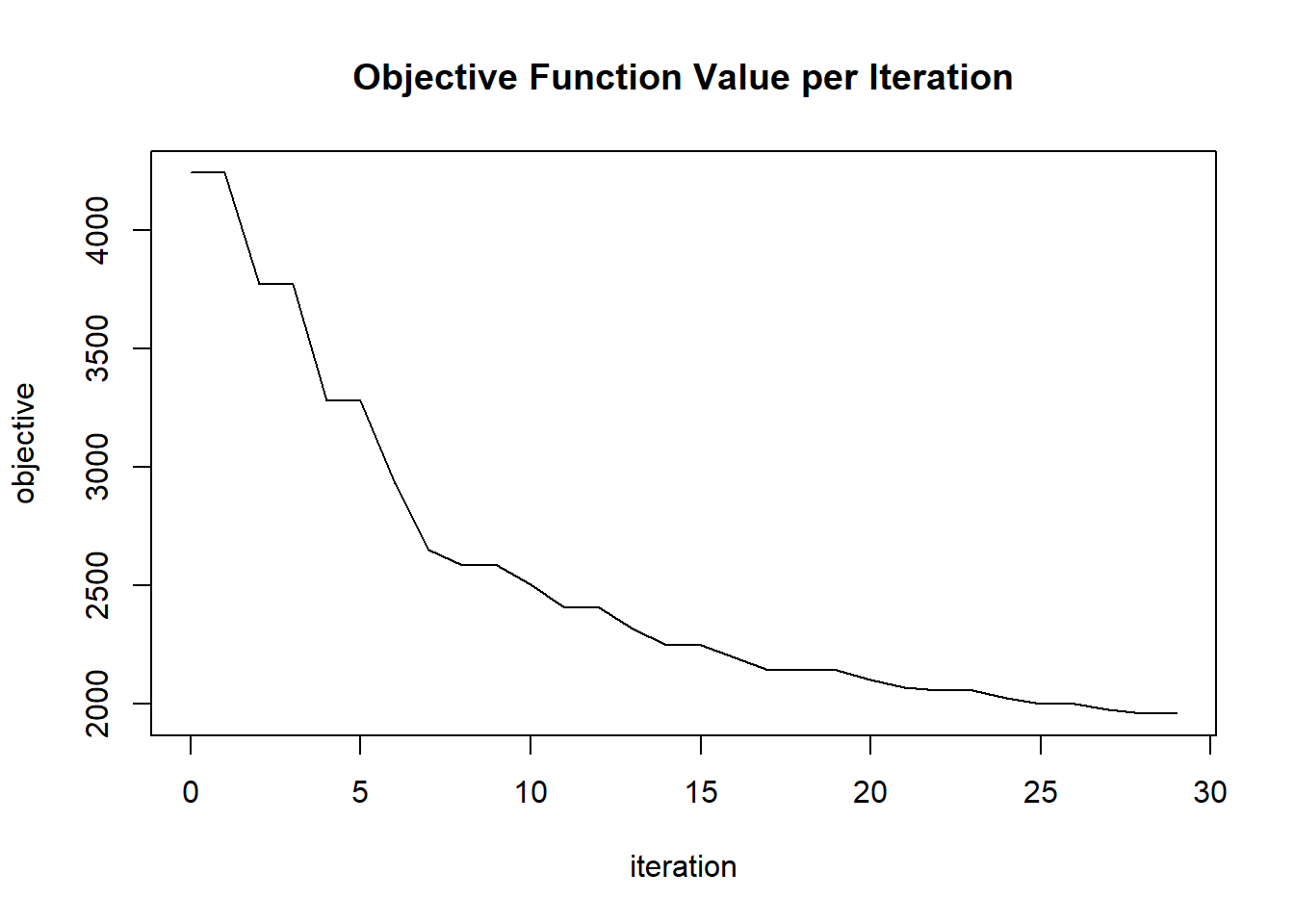
## Iteration 14 of 75 18.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 232 3 L1 Quadratic 4 4 NA NA
## objective
## 232 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_27
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.01855 3059.37324
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1629.755
## Misclassification Error (Categorical): 359
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:28 0.014 sec 0 1.05000 4600.37645
## 2 2020-06-20 06:42:28 0.015 sec 1 0.70000 4600.37645
## 3 2020-06-20 06:42:28 0.017 sec 2 0.73500 3735.98649
## 4 2020-06-20 06:42:28 0.018 sec 3 0.49000 3735.98649
## 5 2020-06-20 06:42:28 0.020 sec 4 0.51450 3573.62975
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:28 0.050 sec 24 0.05678 3071.61341
## 26 2020-06-20 06:42:28 0.051 sec 25 0.03785 3071.61341
## 27 2020-06-20 06:42:28 0.052 sec 26 0.03975 3064.04157
## 28 2020-06-20 06:42:28 0.053 sec 27 0.02650 3064.04157
## 29 2020-06-20 06:42:28 0.055 sec 28 0.02782 3059.37324
## 30 2020-06-20 06:42:28 0.056 sec 29 0.01855 3059.37324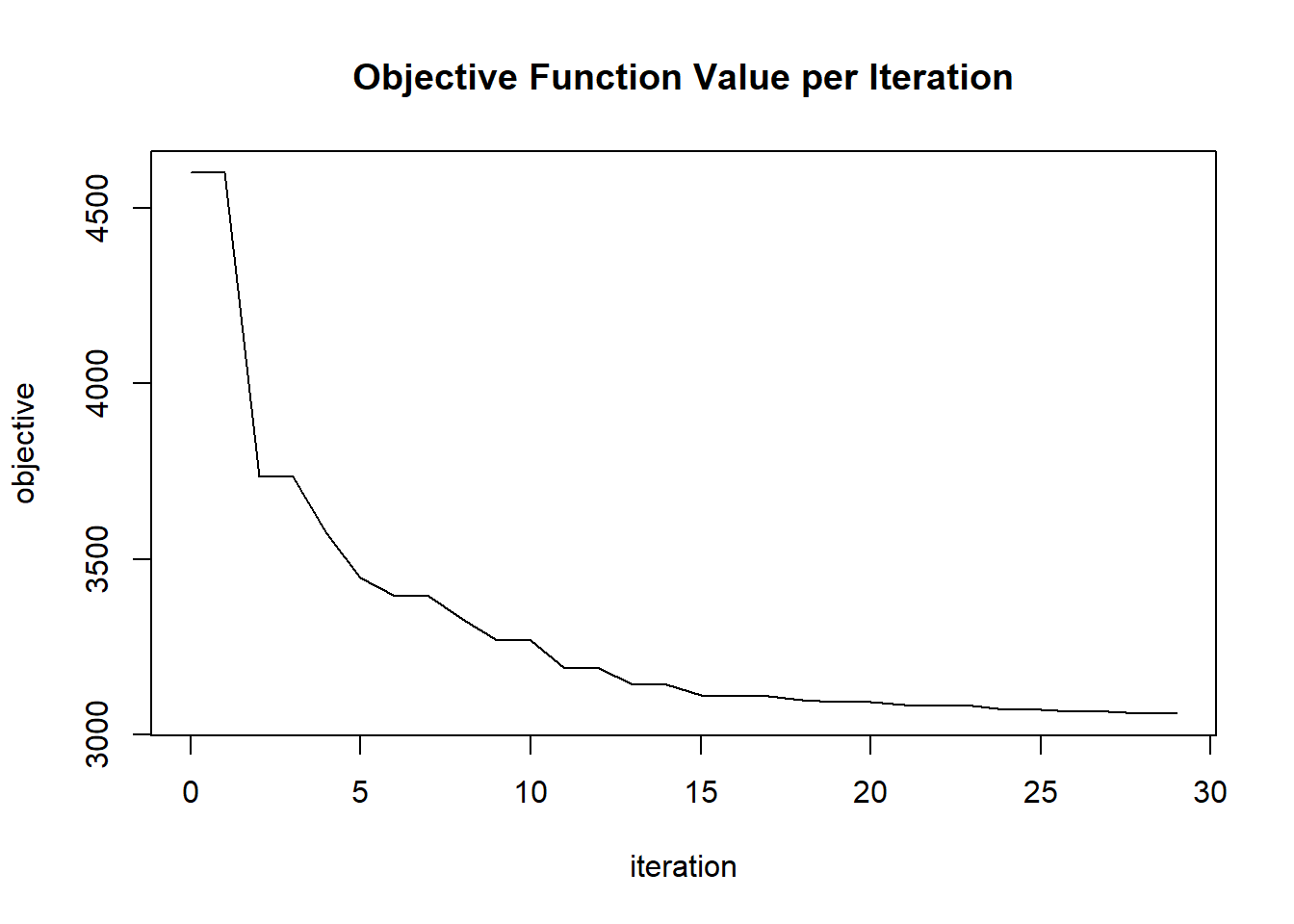
## Iteration 15 of 75 20%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 151 3 L1 Quadratic 4 1 NA NA
## objective
## 151 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_29
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.02921 2719.04642
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1493.146
## Misclassification Error (Categorical): 360
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:29 0.011 sec 0 1.05000 4241.79446
## 2 2020-06-20 06:42:29 0.013 sec 1 0.70000 4241.79446
## 3 2020-06-20 06:42:29 0.014 sec 2 0.46667 4241.79446
## 4 2020-06-20 06:42:29 0.015 sec 3 0.49000 3172.19724
## 5 2020-06-20 06:42:29 0.018 sec 4 0.51450 3119.83804
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:29 0.045 sec 24 0.05678 2732.56924
## 26 2020-06-20 06:42:29 0.046 sec 25 0.05962 2728.80539
## 27 2020-06-20 06:42:29 0.047 sec 26 0.03975 2728.80539
## 28 2020-06-20 06:42:29 0.048 sec 27 0.04173 2723.86288
## 29 2020-06-20 06:42:29 0.049 sec 28 0.04382 2719.04642
## 30 2020-06-20 06:42:29 0.051 sec 29 0.02921 2719.04642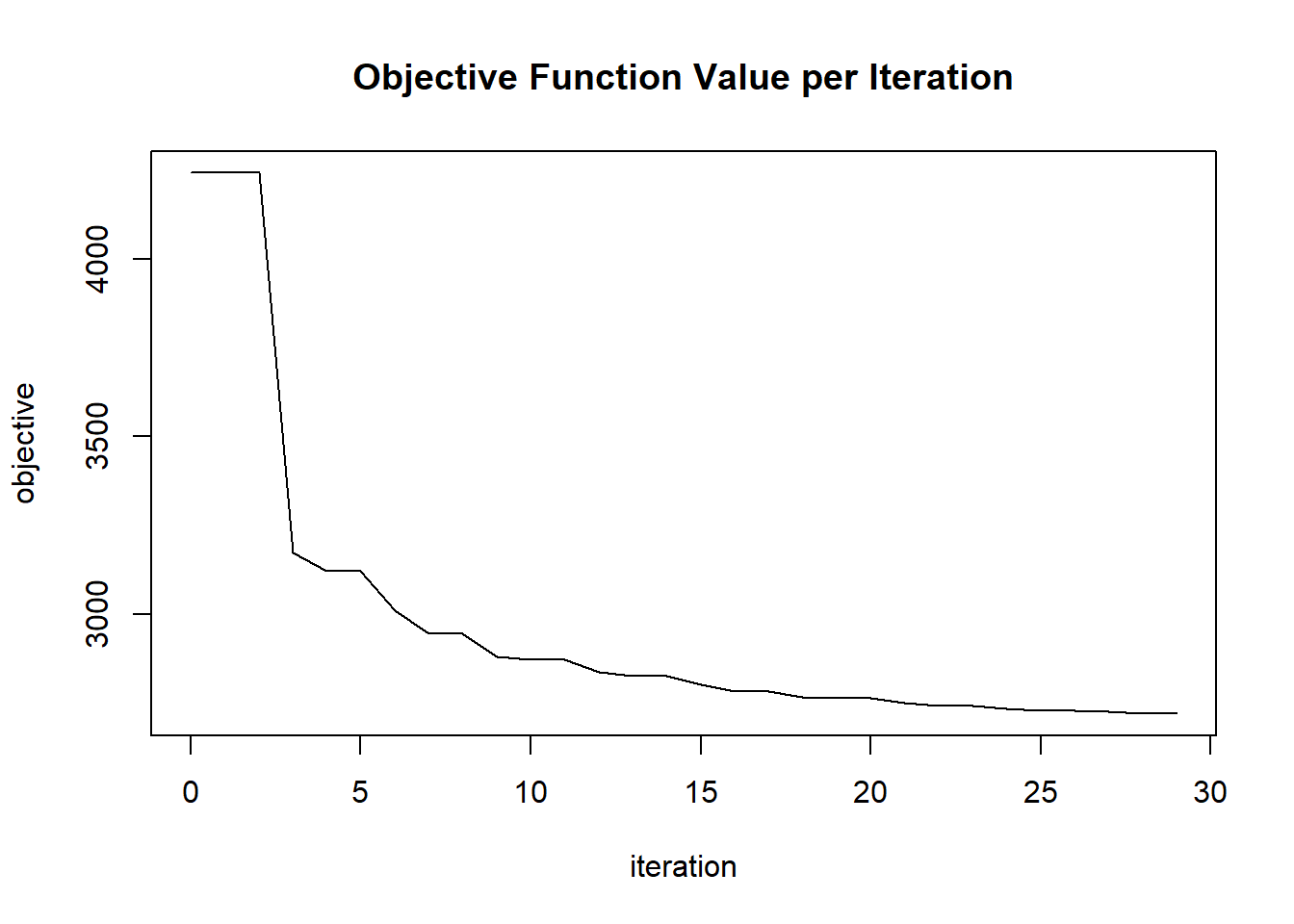
## Iteration 16 of 75 21.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 158 5 Quadratic L1 4 1 NA NA
## objective
## 158 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_31
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 1744.85536
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1309.328
## Misclassification Error (Categorical): 180
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:31 0.018 sec 0 1.05000 2859.22655
## 2 2020-06-20 06:42:31 0.021 sec 1 0.70000 2859.22655
## 3 2020-06-20 06:42:31 0.024 sec 2 0.46667 2859.22655
## 4 2020-06-20 06:42:31 0.026 sec 3 0.31111 2859.22655
## 5 2020-06-20 06:42:31 0.029 sec 4 0.32667 2646.37972
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:31 0.078 sec 24 0.05678 1774.53466
## 26 2020-06-20 06:42:31 0.080 sec 25 0.05962 1763.00949
## 27 2020-06-20 06:42:31 0.082 sec 26 0.06260 1757.75766
## 28 2020-06-20 06:42:31 0.084 sec 27 0.06573 1757.09369
## 29 2020-06-20 06:42:31 0.086 sec 28 0.04382 1757.09369
## 30 2020-06-20 06:42:31 0.088 sec 29 0.04601 1744.85536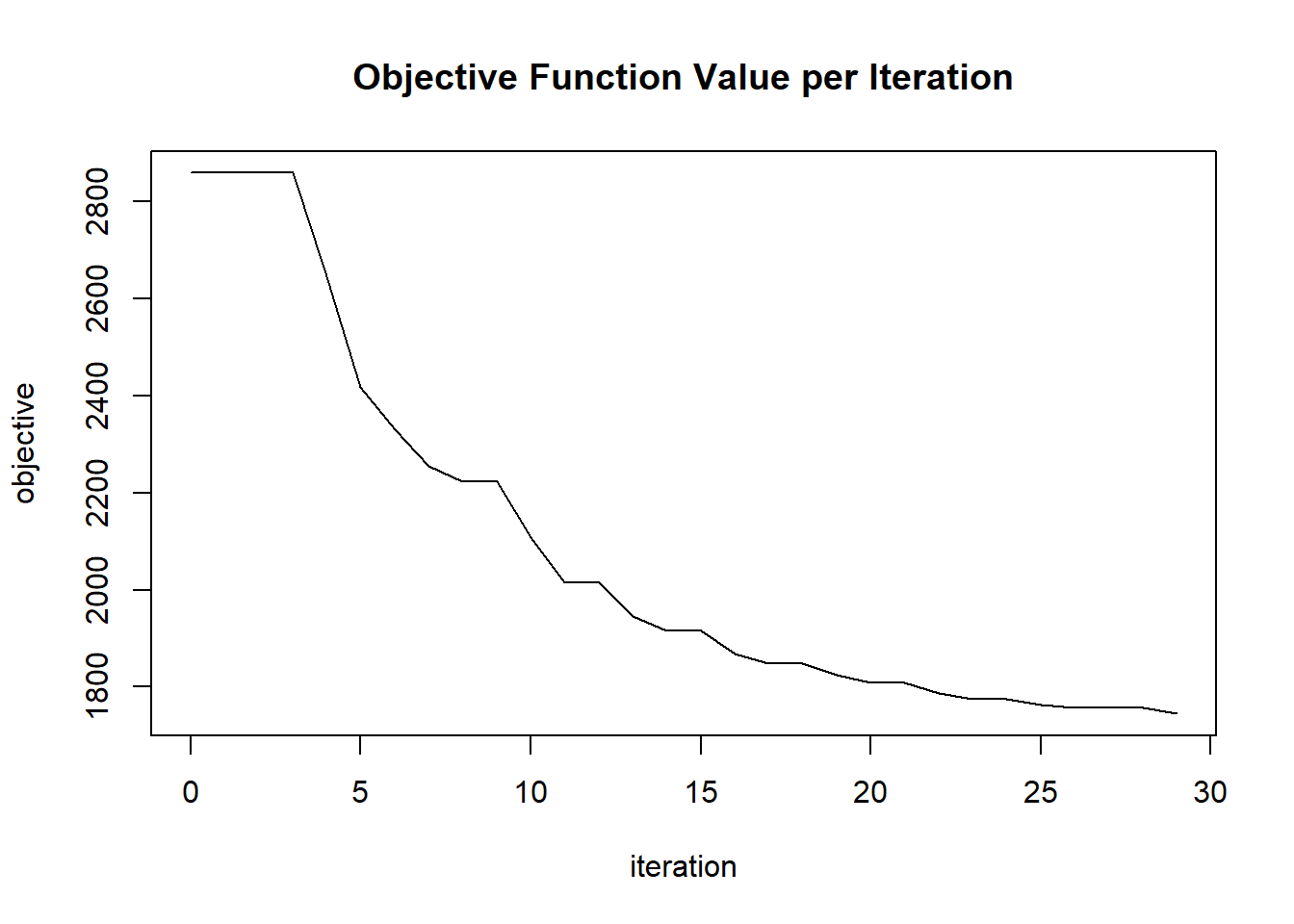
## Iteration 17 of 75 22.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 124 3 L1 Quadratic 1 1 NA NA
## objective
## 124 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_33
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.08560 2314.60930
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1343.625
## Misclassification Error (Categorical): 353
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:33 0.013 sec 0 1.05000 2699.00728
## 2 2020-06-20 06:42:33 0.015 sec 1 0.70000 2699.00728
## 3 2020-06-20 06:42:33 0.017 sec 2 0.46667 2699.00728
## 4 2020-06-20 06:42:33 0.019 sec 3 0.31111 2699.00728
## 5 2020-06-20 06:42:33 0.021 sec 4 0.15556 2699.00728
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:33 0.053 sec 24 0.06707 2325.07536
## 26 2020-06-20 06:42:33 0.055 sec 25 0.07043 2321.23030
## 27 2020-06-20 06:42:33 0.056 sec 26 0.07395 2319.25747
## 28 2020-06-20 06:42:33 0.057 sec 27 0.07765 2317.65464
## 29 2020-06-20 06:42:33 0.059 sec 28 0.08153 2316.28733
## 30 2020-06-20 06:42:33 0.060 sec 29 0.08560 2314.60930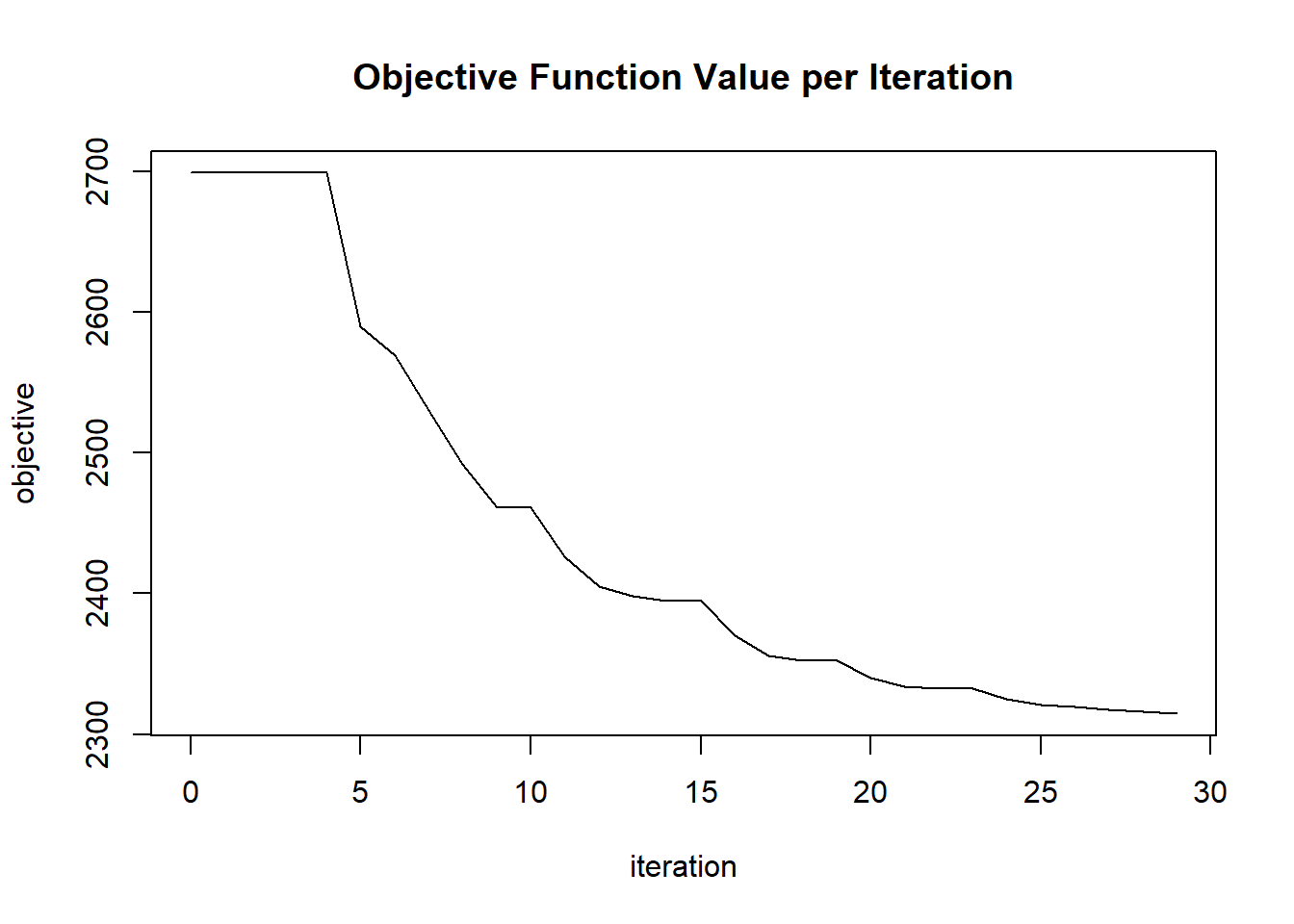
## Iteration 18 of 75 24%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 172 3 None Quadratic 0 4 NA NA
## objective
## 172 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_35
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 2098.79212
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1359.933
## Misclassification Error (Categorical): 339
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:34 0.011 sec 0 1.05000 3134.76905
## 2 2020-06-20 06:42:34 0.013 sec 1 0.70000 3134.76905
## 3 2020-06-20 06:42:34 0.015 sec 2 0.73500 3053.93990
## 4 2020-06-20 06:42:34 0.016 sec 3 0.49000 3053.93990
## 5 2020-06-20 06:42:34 0.018 sec 4 0.51450 2723.05849
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:34 0.050 sec 24 0.05678 2115.19723
## 26 2020-06-20 06:42:34 0.051 sec 25 0.05962 2106.47968
## 27 2020-06-20 06:42:34 0.053 sec 26 0.03975 2106.47968
## 28 2020-06-20 06:42:34 0.054 sec 27 0.04173 2102.54604
## 29 2020-06-20 06:42:34 0.056 sec 28 0.04382 2099.05102
## 30 2020-06-20 06:42:34 0.057 sec 29 0.04601 2098.79212
## Iteration 19 of 75 25.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 214 3 L1 L1 1 4 NA NA
## objective
## 214 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_37
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.13483 2559.79131
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1377.455
## Misclassification Error (Categorical): 345
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:36 0.011 sec 0 1.05000 2924.37776
## 2 2020-06-20 06:42:36 0.012 sec 1 0.70000 2924.37776
## 3 2020-06-20 06:42:36 0.014 sec 2 0.46667 2924.37776
## 4 2020-06-20 06:42:36 0.015 sec 3 0.31111 2924.37776
## 5 2020-06-20 06:42:36 0.017 sec 4 0.15556 2924.37776
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:36 0.040 sec 24 0.10564 2580.67789
## 26 2020-06-20 06:42:36 0.042 sec 25 0.11092 2577.74155
## 27 2020-06-20 06:42:36 0.043 sec 26 0.11647 2570.13709
## 28 2020-06-20 06:42:36 0.044 sec 27 0.12229 2567.53358
## 29 2020-06-20 06:42:36 0.046 sec 28 0.12841 2562.57976
## 30 2020-06-20 06:42:36 0.047 sec 29 0.13483 2559.79131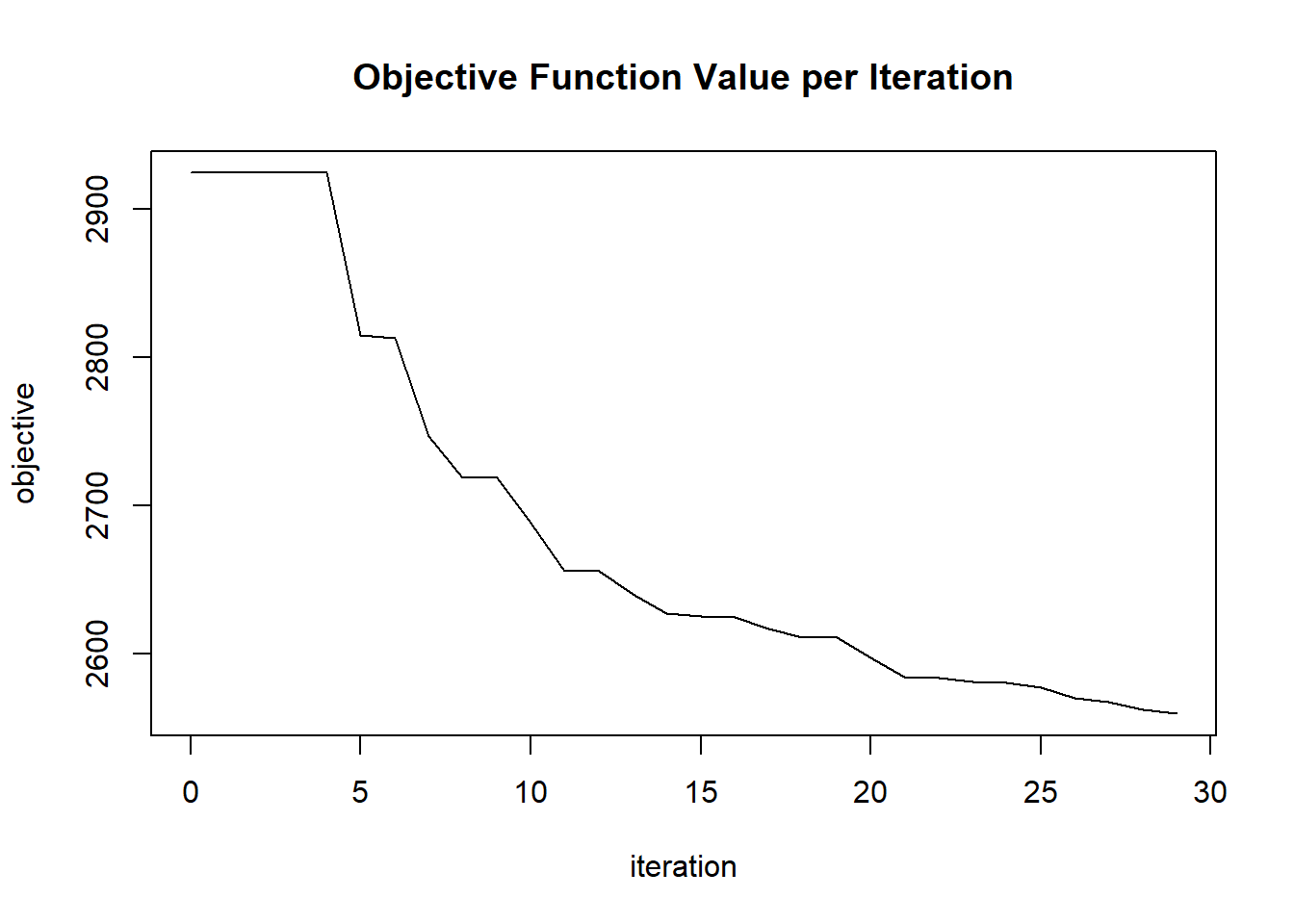
## Iteration 20 of 75 26.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 207 10 L1 Quadratic 1 4 NA NA
## objective
## 207 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_39
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 1928.00010
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 907.1727
## Misclassification Error (Categorical): 99
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:37 0.022 sec 0 1.05000 3662.47013
## 2 2020-06-20 06:42:37 0.025 sec 1 0.70000 3662.47013
## 3 2020-06-20 06:42:37 0.029 sec 2 0.46667 3662.47013
## 4 2020-06-20 06:42:37 0.033 sec 3 0.49000 2923.23653
## 5 2020-06-20 06:42:37 0.037 sec 4 0.51450 2793.94544
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:37 0.118 sec 24 0.14085 1954.54243
## 26 2020-06-20 06:42:37 0.121 sec 25 0.14790 1943.67896
## 27 2020-06-20 06:42:37 0.125 sec 26 0.09860 1943.67896
## 28 2020-06-20 06:42:37 0.129 sec 27 0.10353 1932.56595
## 29 2020-06-20 06:42:37 0.133 sec 28 0.10870 1928.00010
## 30 2020-06-20 06:42:37 0.137 sec 29 0.07247 1928.00010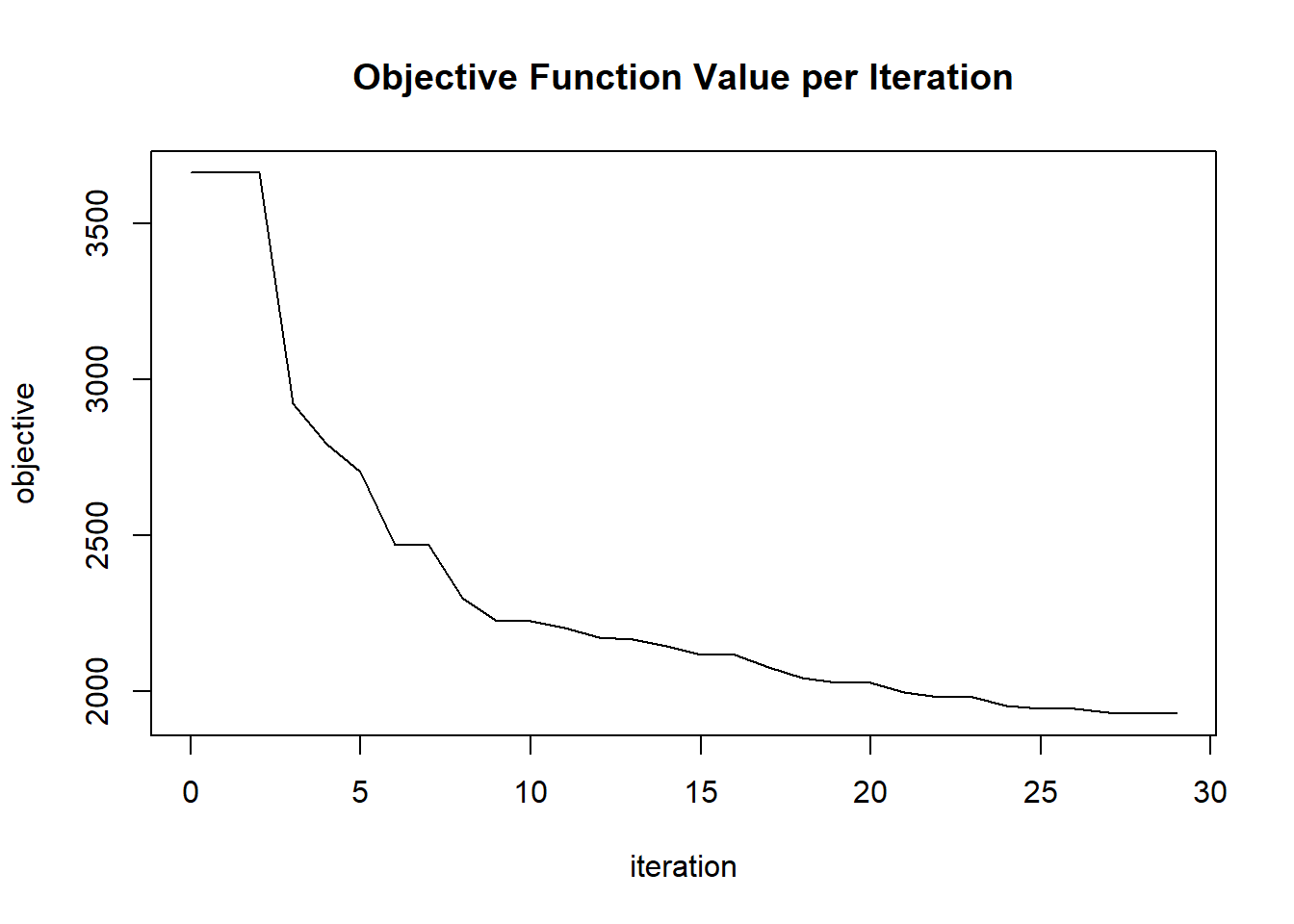
## Iteration 21 of 75 28%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 240 10 Quadratic L1 4 4 NA NA
## objective
## 240 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_41
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.11414 1911.97922
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 898.8717
## Misclassification Error (Categorical): 125
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:39 0.028 sec 0 1.05000 3703.59151
## 2 2020-06-20 06:42:39 0.032 sec 1 0.70000 3703.59151
## 3 2020-06-20 06:42:39 0.037 sec 2 0.46667 3703.59151
## 4 2020-06-20 06:42:39 0.041 sec 3 0.49000 3071.89741
## 5 2020-06-20 06:42:39 0.045 sec 4 0.51450 2805.45177
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:39 0.118 sec 24 0.14085 1977.93400
## 26 2020-06-20 06:42:39 0.123 sec 25 0.14790 1950.59167
## 27 2020-06-20 06:42:39 0.126 sec 26 0.15529 1941.76701
## 28 2020-06-20 06:42:39 0.130 sec 27 0.10353 1941.76701
## 29 2020-06-20 06:42:39 0.133 sec 28 0.10870 1922.02060
## 30 2020-06-20 06:42:39 0.136 sec 29 0.11414 1911.97922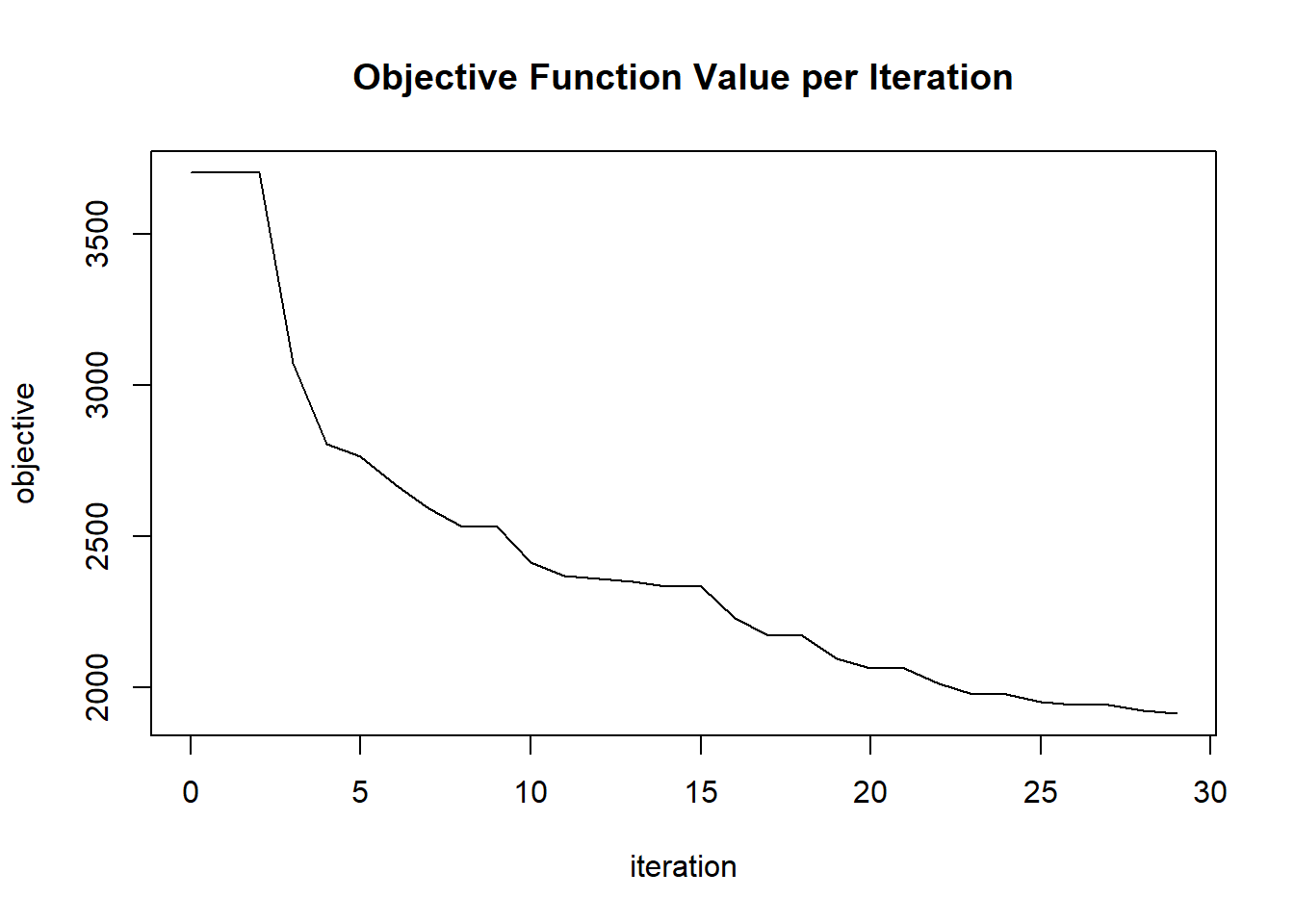
## Iteration 22 of 75 29.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 159 10 Quadratic L1 4 1 NA NA
## objective
## 159 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_43
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 1368.12017
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 677.1681
## Misclassification Error (Categorical): 87
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:40 0.022 sec 0 1.05000 3007.94952
## 2 2020-06-20 06:42:40 0.027 sec 1 0.70000 3007.94952
## 3 2020-06-20 06:42:40 0.032 sec 2 0.46667 3007.94952
## 4 2020-06-20 06:42:41 0.037 sec 3 0.49000 2659.83009
## 5 2020-06-20 06:42:41 0.042 sec 4 0.51450 2348.06378
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:41 0.108 sec 24 0.14085 1395.58157
## 26 2020-06-20 06:42:41 0.111 sec 25 0.09390 1395.58157
## 27 2020-06-20 06:42:41 0.115 sec 26 0.09860 1373.02331
## 28 2020-06-20 06:42:41 0.119 sec 27 0.10353 1368.35303
## 29 2020-06-20 06:42:41 0.123 sec 28 0.10870 1368.12017
## 30 2020-06-20 06:42:41 0.126 sec 29 0.07247 1368.12017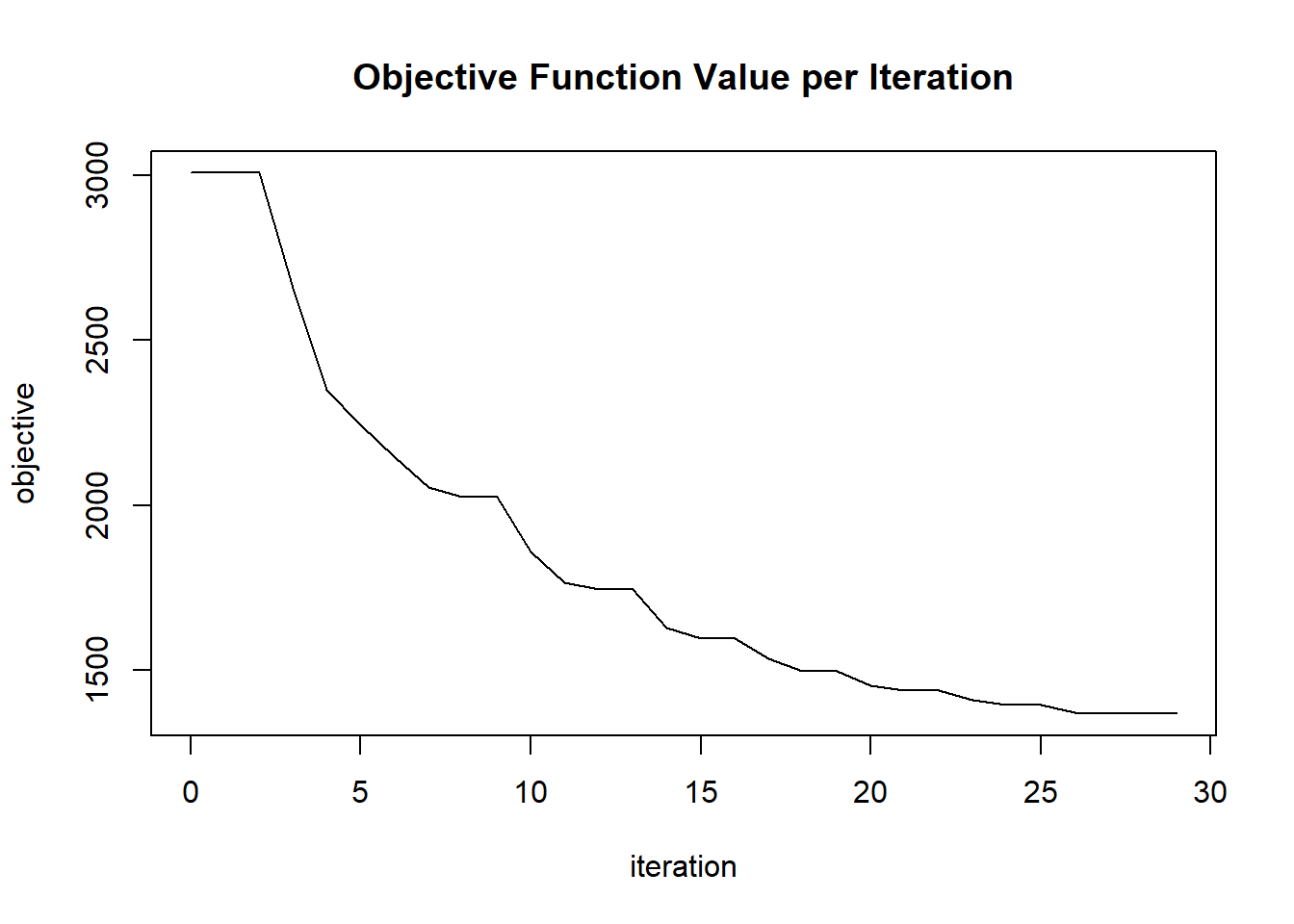
## Iteration 23 of 75 30.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 234 10 L1 Quadratic 4 4 NA NA
## objective
## 234 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_45
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 3097.74184
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1577.28
## Misclassification Error (Categorical): 258
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:42 0.018 sec 0 1.05000 4888.30984
## 2 2020-06-20 06:42:42 0.023 sec 1 1.10250 4523.25134
## 3 2020-06-20 06:42:42 0.027 sec 2 0.73500 4523.25134
## 4 2020-06-20 06:42:42 0.031 sec 3 0.49000 4523.25134
## 5 2020-06-20 06:42:42 0.037 sec 4 0.51450 4062.66421
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:42 0.105 sec 24 0.14085 3125.30525
## 26 2020-06-20 06:42:42 0.109 sec 25 0.14790 3122.95615
## 27 2020-06-20 06:42:42 0.112 sec 26 0.09860 3122.95615
## 28 2020-06-20 06:42:42 0.115 sec 27 0.10353 3103.47638
## 29 2020-06-20 06:42:42 0.118 sec 28 0.10870 3097.74184
## 30 2020-06-20 06:42:42 0.121 sec 29 0.07247 3097.74184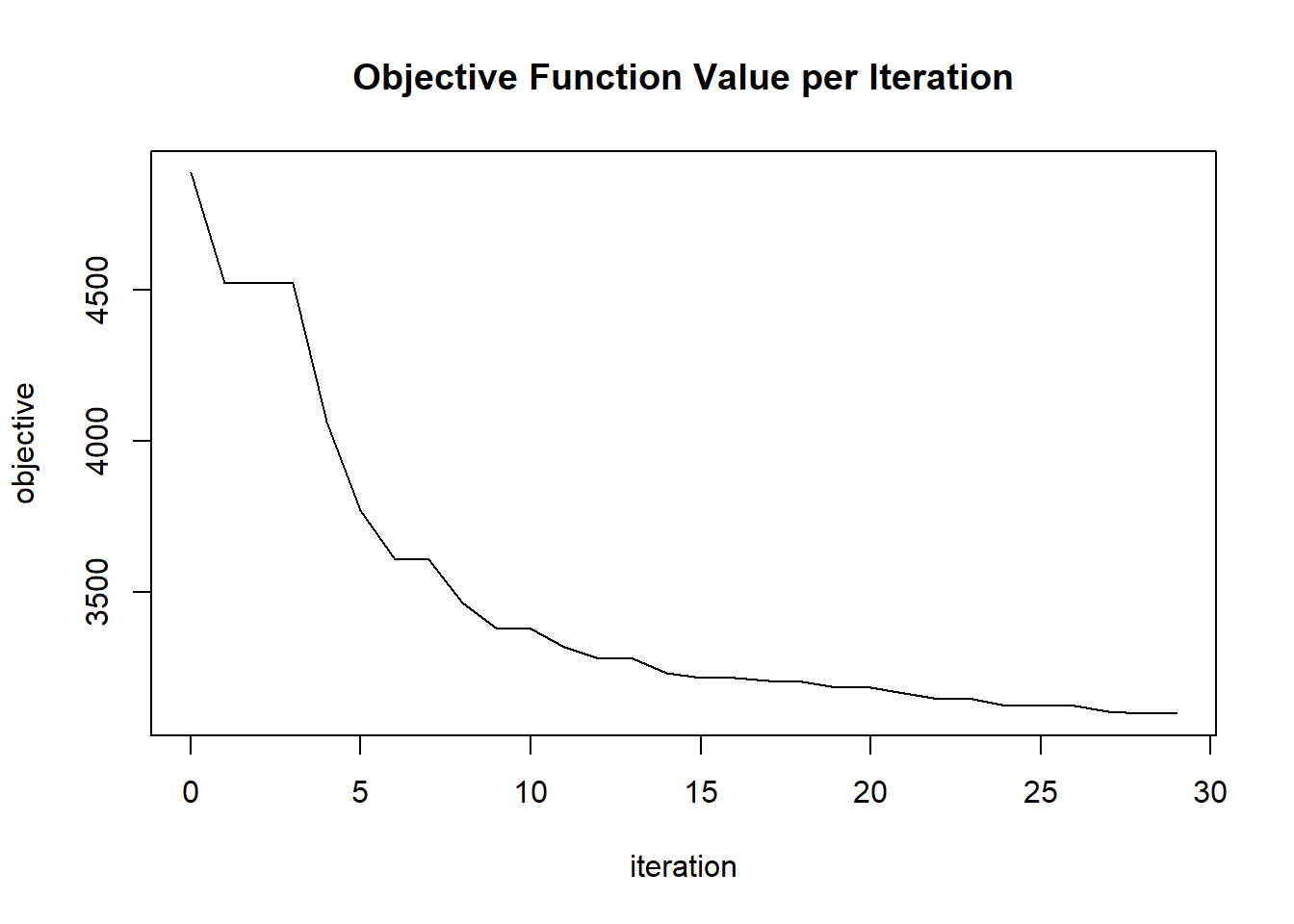
## Iteration 24 of 75 32%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 161 5 L1 L1 4 1 NA NA
## objective
## 161 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_47
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 2416.52572
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1419.86
## Misclassification Error (Categorical): 261
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:44 0.024 sec 0 1.05000 4449.74084
## 2 2020-06-20 06:42:44 0.026 sec 1 0.70000 4449.74084
## 3 2020-06-20 06:42:44 0.029 sec 2 0.73500 3723.18153
## 4 2020-06-20 06:42:44 0.031 sec 3 0.49000 3723.18153
## 5 2020-06-20 06:42:44 0.034 sec 4 0.51450 3319.63788
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:44 0.094 sec 24 0.08943 2447.75348
## 26 2020-06-20 06:42:44 0.097 sec 25 0.09390 2442.79407
## 27 2020-06-20 06:42:44 0.099 sec 26 0.06260 2442.79407
## 28 2020-06-20 06:42:44 0.101 sec 27 0.06573 2429.09068
## 29 2020-06-20 06:42:44 0.103 sec 28 0.06902 2416.52572
## 30 2020-06-20 06:42:44 0.105 sec 29 0.04601 2416.52572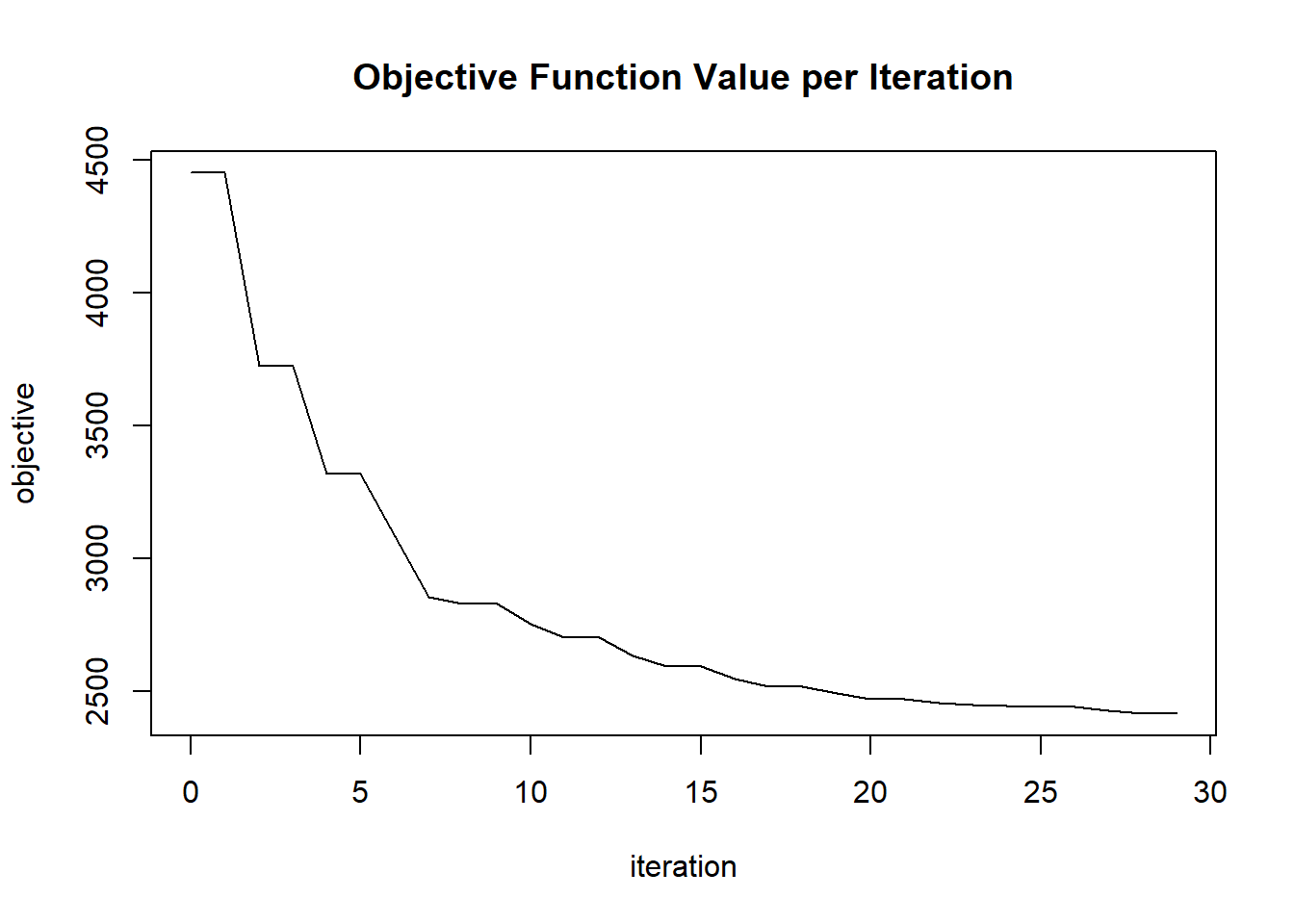
## Iteration 25 of 75 33.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 216 10 L1 L1 1 4 NA NA
## objective
## 216 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_49
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 1772.02475
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 718.659
## Misclassification Error (Categorical): 67
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:45 0.017 sec 0 1.05000 3769.59059
## 2 2020-06-20 06:42:45 0.020 sec 1 0.70000 3769.59059
## 3 2020-06-20 06:42:45 0.025 sec 2 0.46667 3769.59059
## 4 2020-06-20 06:42:45 0.029 sec 3 0.49000 3196.92762
## 5 2020-06-20 06:42:45 0.033 sec 4 0.51450 2852.78647
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:45 0.096 sec 24 0.34941 1807.26389
## 26 2020-06-20 06:42:45 0.099 sec 25 0.23294 1807.26389
## 27 2020-06-20 06:42:45 0.102 sec 26 0.24458 1781.30373
## 28 2020-06-20 06:42:45 0.106 sec 27 0.25681 1773.04977
## 29 2020-06-20 06:42:45 0.110 sec 28 0.26965 1772.02475
## 30 2020-06-20 06:42:45 0.114 sec 29 0.17977 1772.02475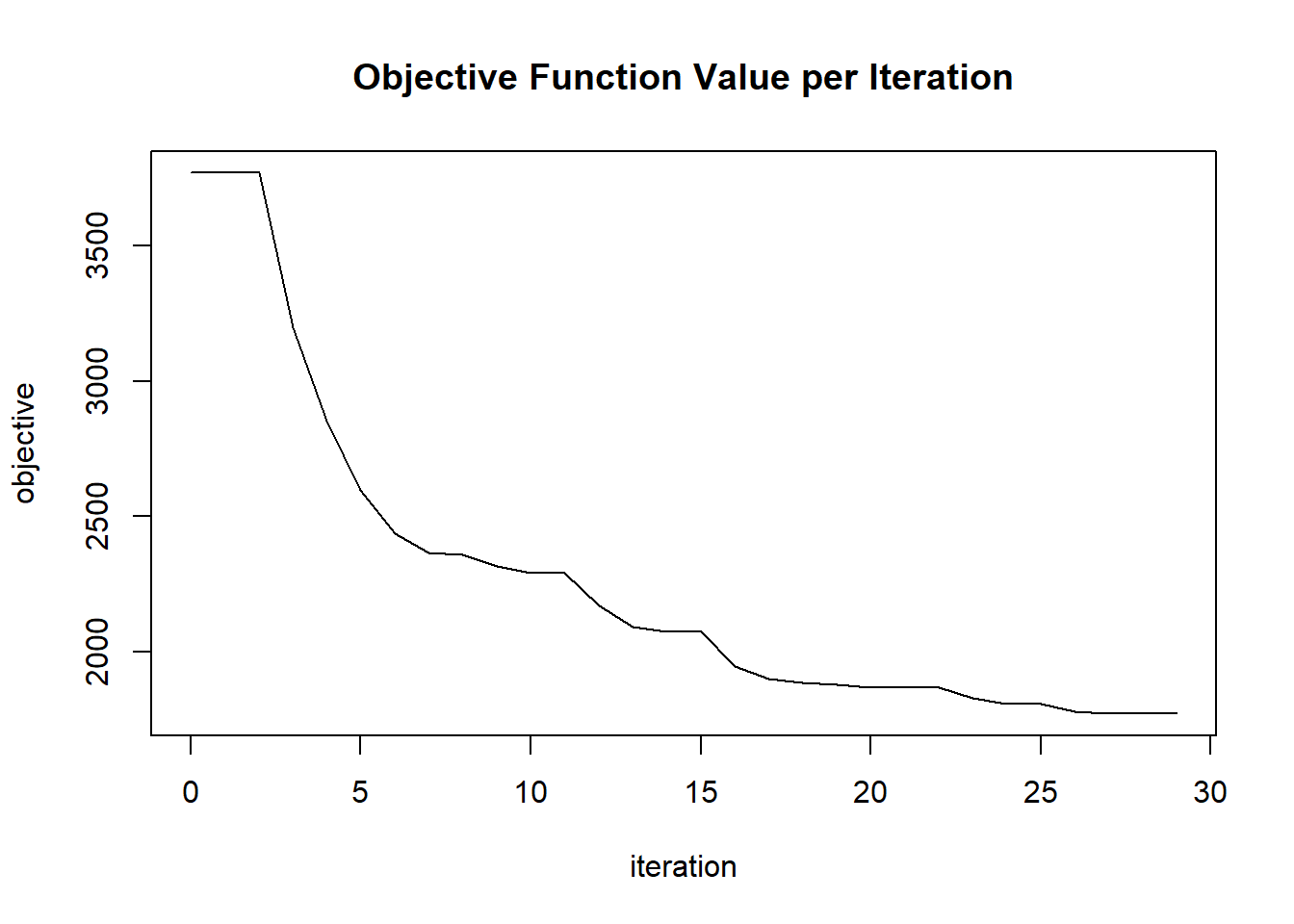
## Iteration 26 of 75 34.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 135 10 L1 L1 1 1 NA NA
## objective
## 135 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_51
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.11414 1252.36736
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 611.2258
## Misclassification Error (Categorical): 50
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:47 0.023 sec 0 1.05000 3107.65051
## 2 2020-06-20 06:42:47 0.028 sec 1 0.70000 3107.65051
## 3 2020-06-20 06:42:47 0.033 sec 2 0.46667 3107.65051
## 4 2020-06-20 06:42:47 0.037 sec 3 0.49000 3045.91653
## 5 2020-06-20 06:42:47 0.040 sec 4 0.51450 2703.91261
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:47 0.110 sec 24 0.22184 1289.71785
## 26 2020-06-20 06:42:47 0.113 sec 25 0.14790 1289.71785
## 27 2020-06-20 06:42:47 0.116 sec 26 0.15529 1274.07942
## 28 2020-06-20 06:42:47 0.119 sec 27 0.16306 1265.16554
## 29 2020-06-20 06:42:47 0.122 sec 28 0.10870 1265.16554
## 30 2020-06-20 06:42:47 0.125 sec 29 0.11414 1252.36736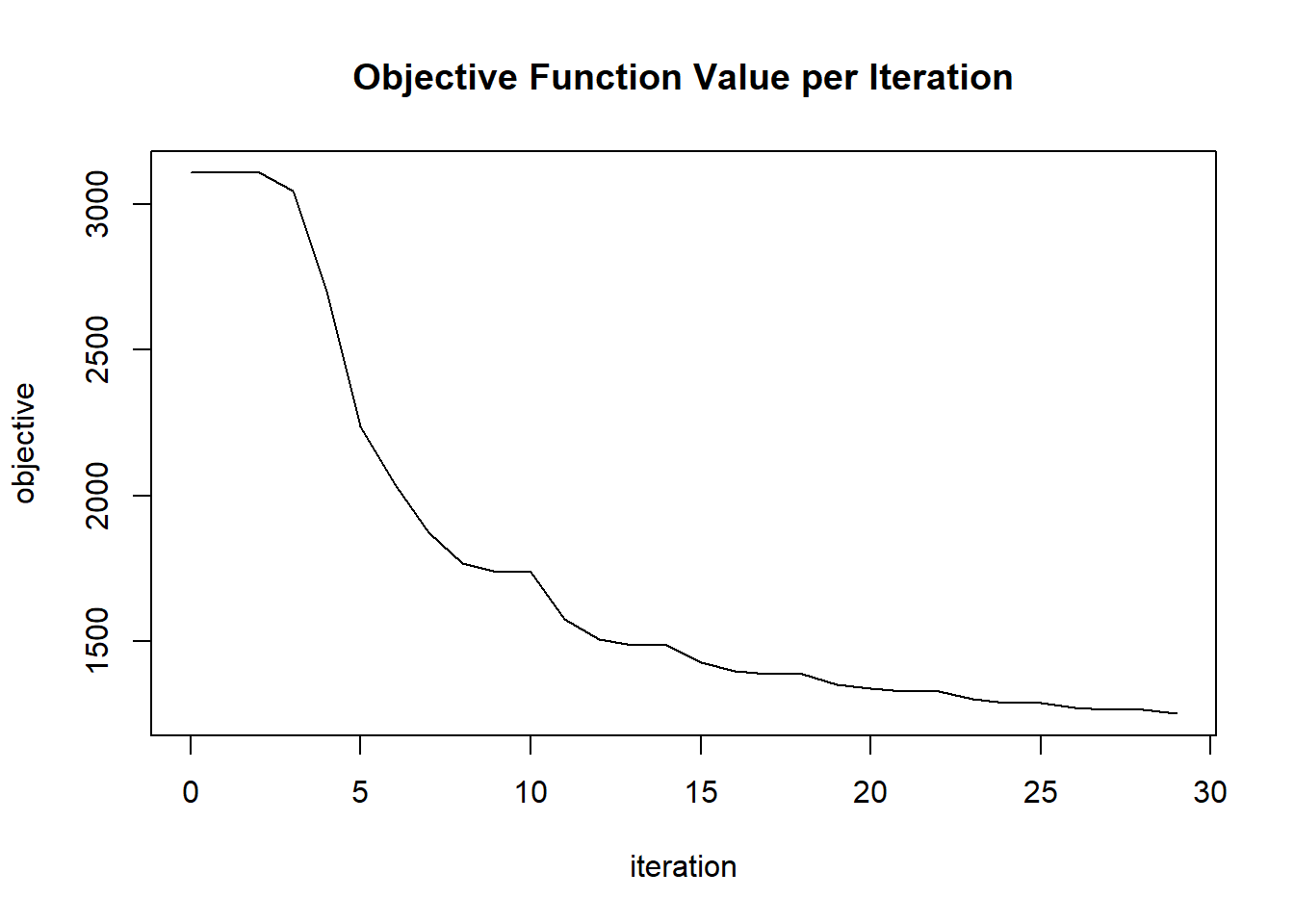
## Iteration 27 of 75 36%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 101 5 None L1 0 1 NA NA
## objective
## 101 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_53
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.33445 1177.62532
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1434.829
## Misclassification Error (Categorical): 95
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:48 0.012 sec 0 1.05000 2385.75844
## 2 2020-06-20 06:42:48 0.014 sec 1 0.70000 2385.75844
## 3 2020-06-20 06:42:48 0.015 sec 2 0.46667 2385.75844
## 4 2020-06-20 06:42:48 0.017 sec 3 0.31111 2385.75844
## 5 2020-06-20 06:42:48 0.019 sec 4 0.15556 2385.75844
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:48 0.056 sec 24 0.41274 1286.26662
## 26 2020-06-20 06:42:48 0.058 sec 25 0.43337 1259.55898
## 27 2020-06-20 06:42:48 0.060 sec 26 0.45504 1237.60458
## 28 2020-06-20 06:42:48 0.061 sec 27 0.47779 1228.32777
## 29 2020-06-20 06:42:48 0.063 sec 28 0.31853 1228.32777
## 30 2020-06-20 06:42:48 0.065 sec 29 0.33445 1177.62532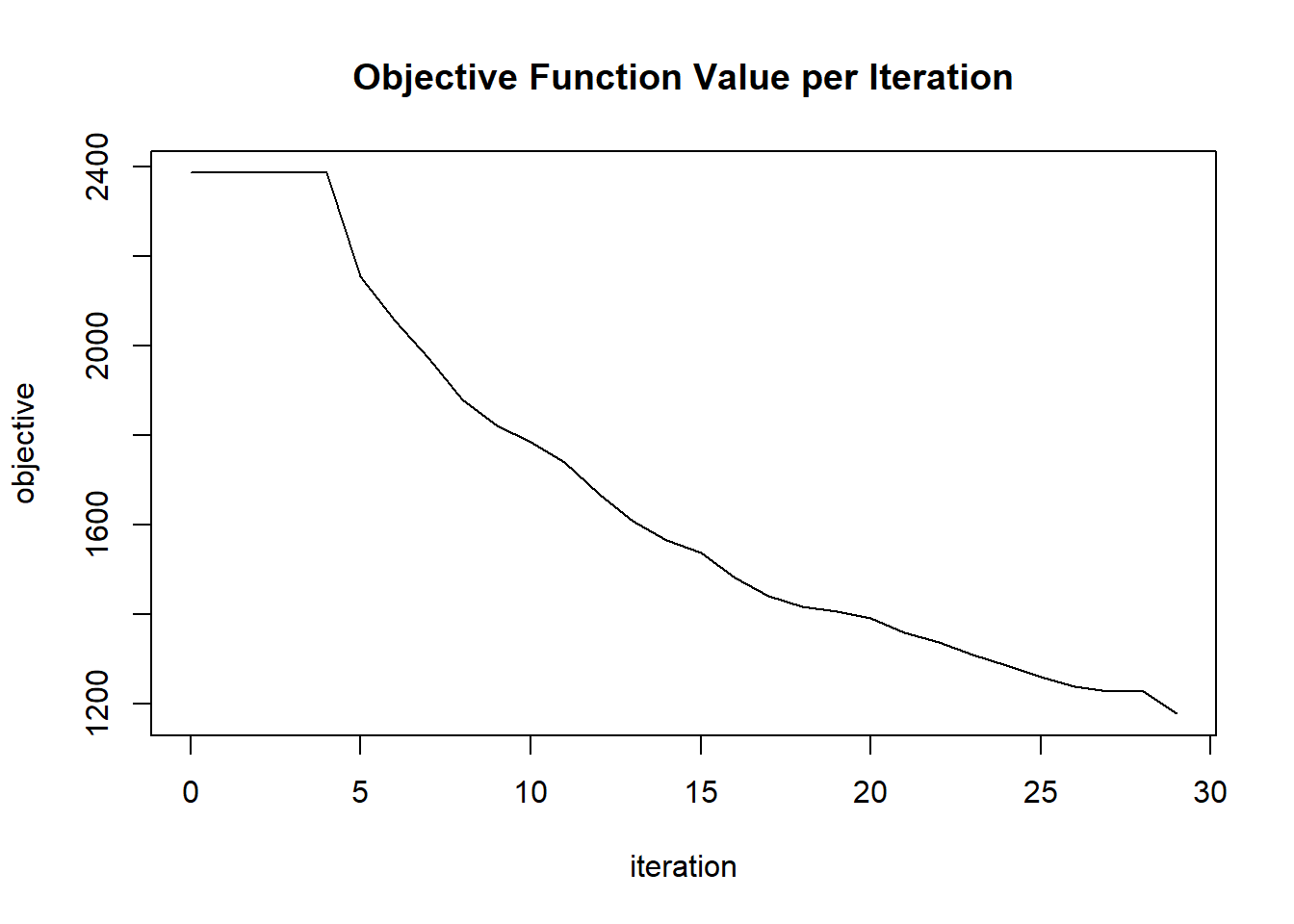
## Iteration 28 of 75 37.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 149 5 Quadratic Quadratic 4 1 NA NA
## objective
## 149 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_55
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 1931.61877
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1346.045
## Misclassification Error (Categorical): 173
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:50 0.016 sec 0 1.05000 3016.58214
## 2 2020-06-20 06:42:50 0.017 sec 1 0.70000 3016.58214
## 3 2020-06-20 06:42:50 0.019 sec 2 0.46667 3016.58214
## 4 2020-06-20 06:42:50 0.021 sec 3 0.49000 2851.17913
## 5 2020-06-20 06:42:50 0.023 sec 4 0.51450 2507.73659
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:50 0.064 sec 24 0.08943 1951.85283
## 26 2020-06-20 06:42:50 0.065 sec 25 0.09390 1945.27278
## 27 2020-06-20 06:42:50 0.067 sec 26 0.06260 1945.27278
## 28 2020-06-20 06:42:50 0.069 sec 27 0.06573 1936.11036
## 29 2020-06-20 06:42:50 0.071 sec 28 0.06902 1931.61877
## 30 2020-06-20 06:42:50 0.073 sec 29 0.04601 1931.61877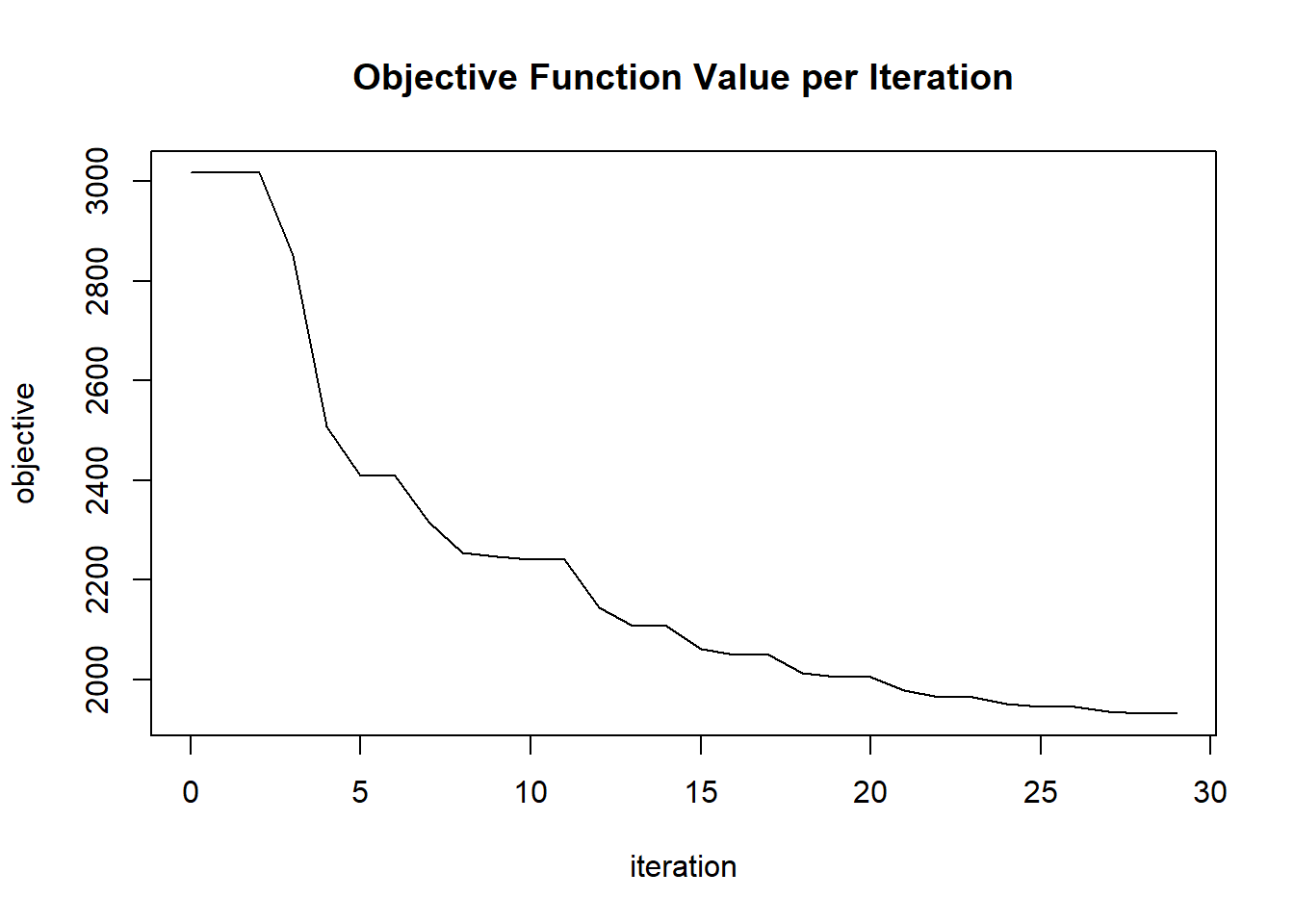
## Iteration 29 of 75 38.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 33 10 Quadratic None 1 0 NA NA
## objective
## 33 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_57
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 681.11182
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 559.3386
## Misclassification Error (Categorical): 44
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:52 0.042 sec 0 1.05000 2777.66708
## 2 2020-06-20 06:42:52 0.047 sec 1 0.70000 2777.66708
## 3 2020-06-20 06:42:52 0.055 sec 2 0.46667 2777.66708
## 4 2020-06-20 06:42:52 0.060 sec 3 0.31111 2777.66708
## 5 2020-06-20 06:42:52 0.064 sec 4 0.32667 2009.62535
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:52 0.143 sec 24 0.22184 743.00722
## 26 2020-06-20 06:42:52 0.146 sec 25 0.23294 722.05962
## 27 2020-06-20 06:42:52 0.150 sec 26 0.24458 720.93798
## 28 2020-06-20 06:42:52 0.154 sec 27 0.16306 720.93798
## 29 2020-06-20 06:42:52 0.157 sec 28 0.17121 692.39390
## 30 2020-06-20 06:42:52 0.161 sec 29 0.17977 681.11182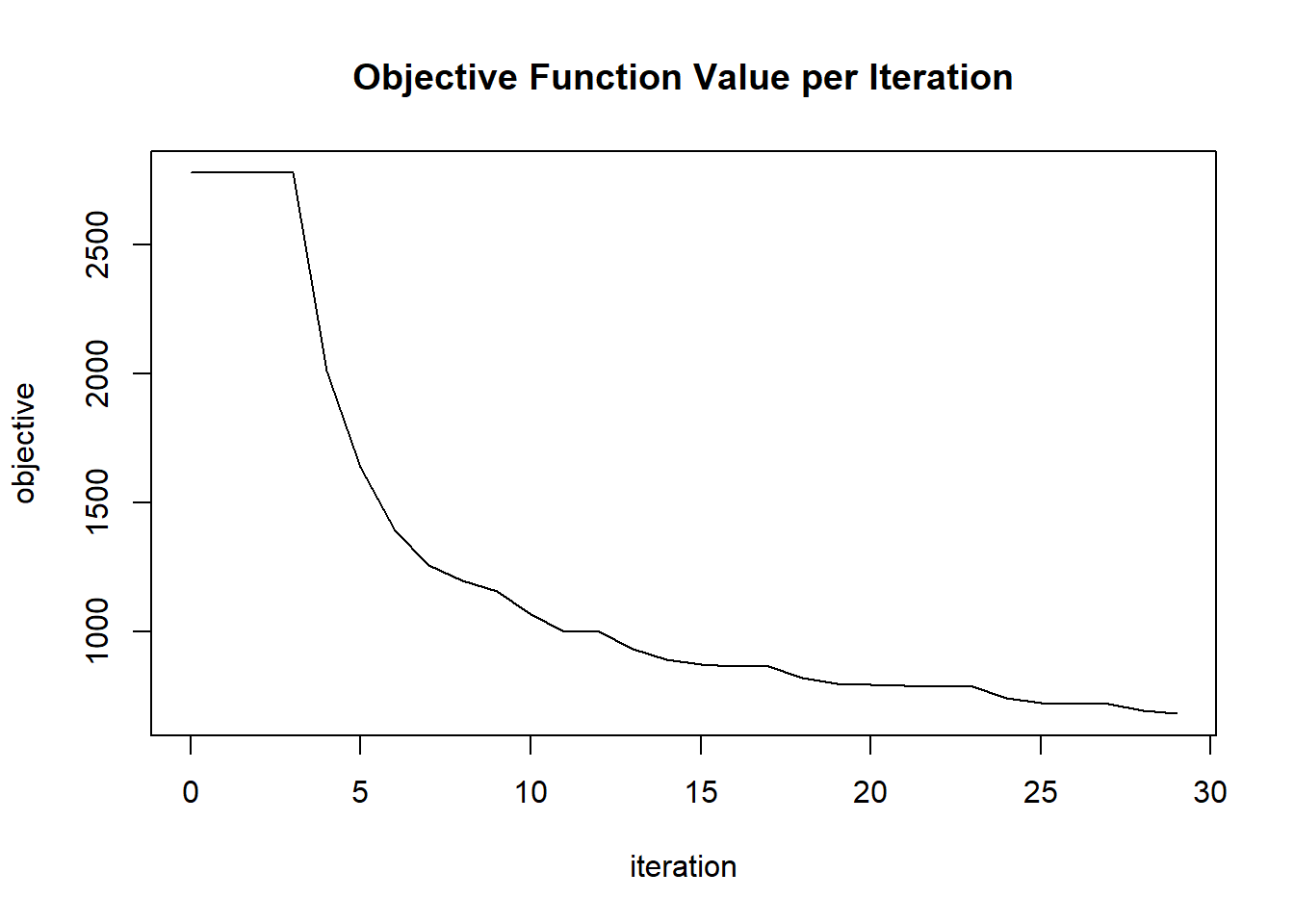
## Iteration 30 of 75 40%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 58 3 Quadratic None 4 0 NA NA
## objective
## 58 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_59
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.03451 2137.97996
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1342.545
## Misclassification Error (Categorical): 355
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:53 0.011 sec 0 1.05000 2521.45078
## 2 2020-06-20 06:42:53 0.012 sec 1 0.70000 2521.45078
## 3 2020-06-20 06:42:53 0.014 sec 2 0.46667 2521.45078
## 4 2020-06-20 06:42:53 0.015 sec 3 0.31111 2521.45078
## 5 2020-06-20 06:42:53 0.016 sec 4 0.15556 2521.45078
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:53 0.039 sec 24 0.04259 2148.31707
## 26 2020-06-20 06:42:53 0.041 sec 25 0.04472 2147.07827
## 27 2020-06-20 06:42:53 0.042 sec 26 0.04695 2145.09626
## 28 2020-06-20 06:42:53 0.043 sec 27 0.03130 2145.09626
## 29 2020-06-20 06:42:53 0.045 sec 28 0.03287 2138.99783
## 30 2020-06-20 06:42:53 0.046 sec 29 0.03451 2137.97996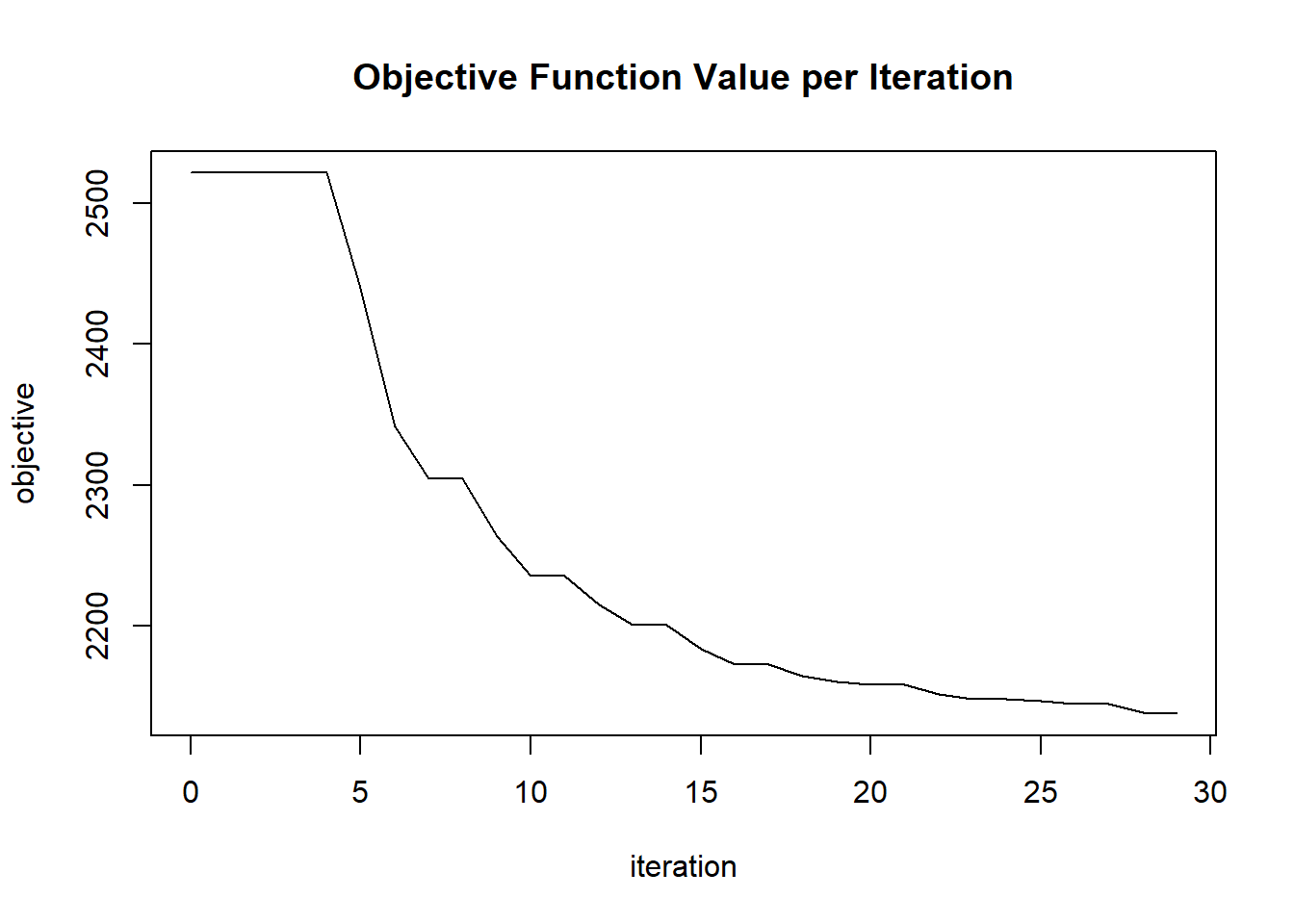
## Iteration 31 of 75 41.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 231 10 Quadratic Quadratic 4 4 NA NA
## objective
## 231 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_61
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.02921 2299.44292
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1194.597
## Misclassification Error (Categorical): 129
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:55 0.030 sec 0 1.05000 3706.85791
## 2 2020-06-20 06:42:55 0.034 sec 1 0.70000 3706.85791
## 3 2020-06-20 06:42:55 0.039 sec 2 0.73500 3491.52619
## 4 2020-06-20 06:42:55 0.044 sec 3 0.77175 3226.04579
## 5 2020-06-20 06:42:55 0.048 sec 4 0.81034 3219.54303
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:55 0.142 sec 24 0.08943 2319.50966
## 26 2020-06-20 06:42:55 0.146 sec 25 0.05962 2319.50966
## 27 2020-06-20 06:42:55 0.150 sec 26 0.06260 2306.58959
## 28 2020-06-20 06:42:55 0.153 sec 27 0.04173 2306.58959
## 29 2020-06-20 06:42:55 0.156 sec 28 0.04382 2299.44292
## 30 2020-06-20 06:42:55 0.160 sec 29 0.02921 2299.44292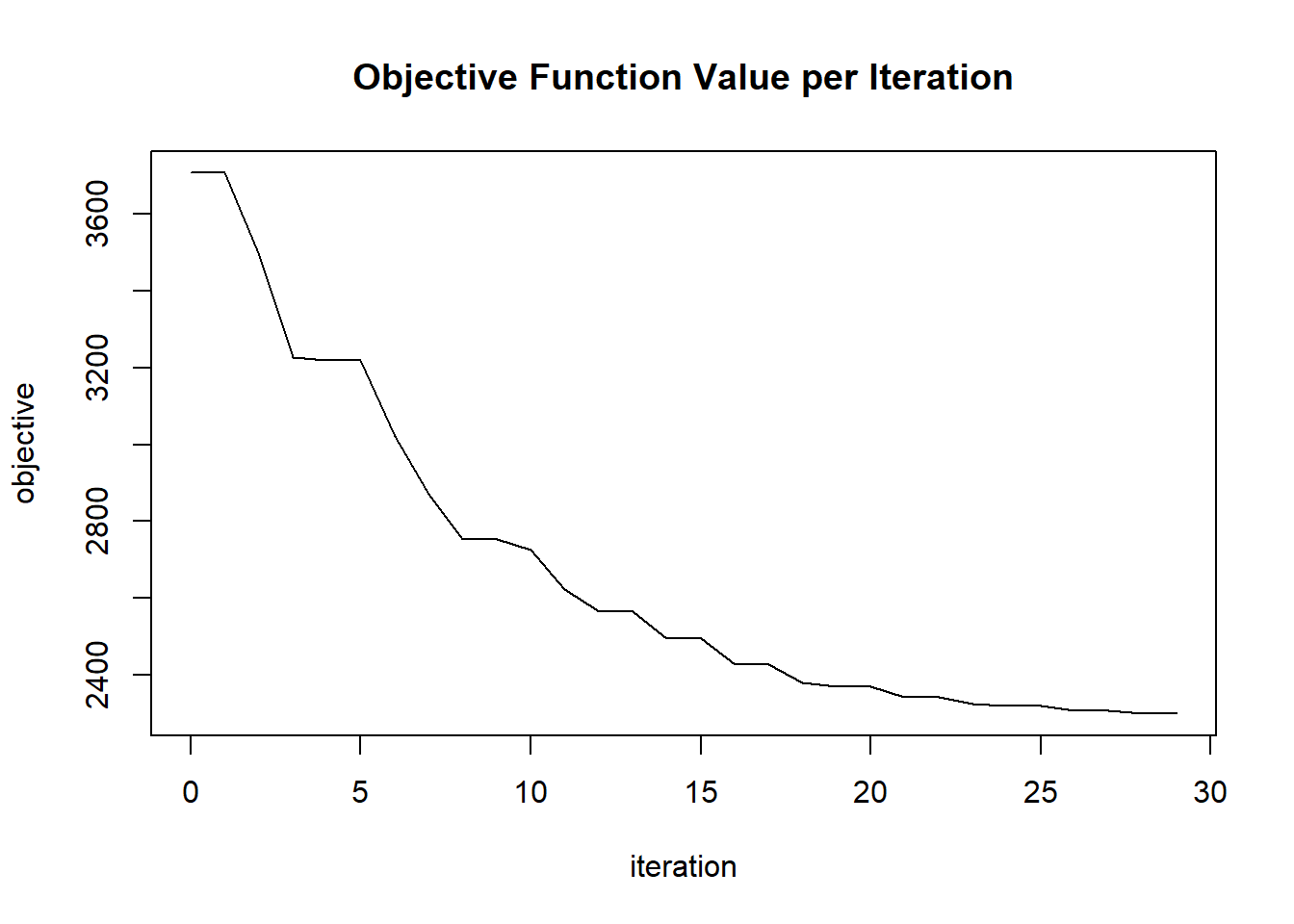
## Iteration 32 of 75 42.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 152 5 L1 Quadratic 4 1 NA NA
## objective
## 152 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_63
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 2564.77247
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1471.568
## Misclassification Error (Categorical): 256
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:56 0.016 sec 0 1.05000 4487.48202
## 2 2020-06-20 06:42:56 0.019 sec 1 0.70000 4487.48202
## 3 2020-06-20 06:42:56 0.021 sec 2 0.73500 3612.17655
## 4 2020-06-20 06:42:56 0.024 sec 3 0.49000 3612.17655
## 5 2020-06-20 06:42:56 0.025 sec 4 0.51450 3424.12459
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:56 0.068 sec 24 0.08943 2593.95334
## 26 2020-06-20 06:42:56 0.070 sec 25 0.09390 2586.73186
## 27 2020-06-20 06:42:56 0.072 sec 26 0.06260 2586.73186
## 28 2020-06-20 06:42:56 0.074 sec 27 0.06573 2572.14357
## 29 2020-06-20 06:42:56 0.077 sec 28 0.06902 2564.77247
## 30 2020-06-20 06:42:56 0.079 sec 29 0.04601 2564.77247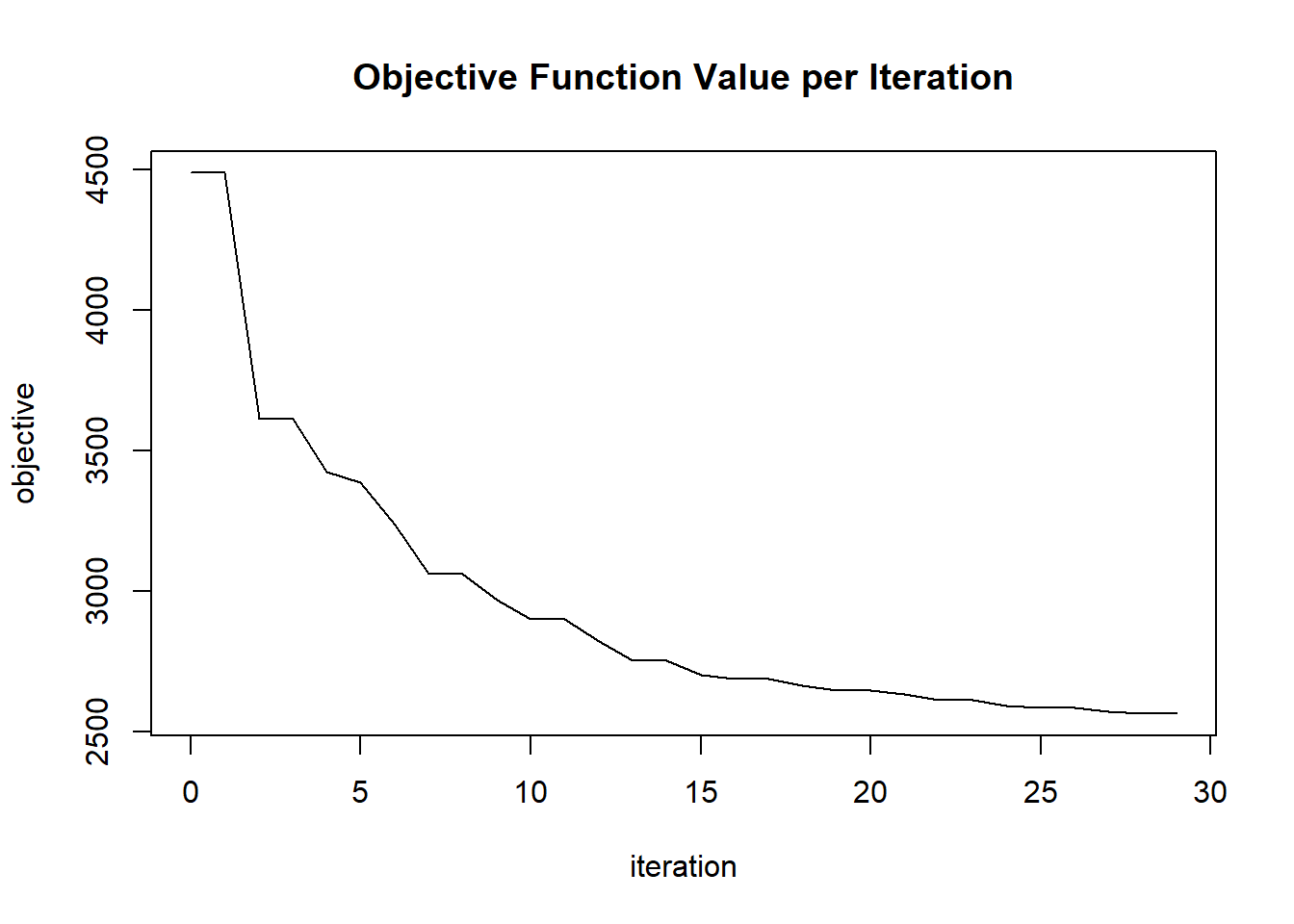
## Iteration 33 of 75 44%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 181 3 None L1 0 4 NA NA
## objective
## 181 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_65
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 2081.97962
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1562.542
## Misclassification Error (Categorical): 263
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:42:58 0.011 sec 0 1.05000 2981.05265
## 2 2020-06-20 06:42:58 0.012 sec 1 0.70000 2981.05265
## 3 2020-06-20 06:42:58 0.014 sec 2 0.46667 2981.05265
## 4 2020-06-20 06:42:58 0.016 sec 3 0.31111 2981.05265
## 5 2020-06-20 06:42:58 0.018 sec 4 0.32667 2961.15593
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:42:58 0.050 sec 24 0.22184 2147.31713
## 26 2020-06-20 06:42:58 0.052 sec 25 0.23294 2112.08129
## 27 2020-06-20 06:42:58 0.053 sec 26 0.24458 2101.64469
## 28 2020-06-20 06:42:58 0.056 sec 27 0.25681 2092.79617
## 29 2020-06-20 06:42:58 0.057 sec 28 0.26965 2081.97962
## 30 2020-06-20 06:42:58 0.059 sec 29 0.17977 2081.97962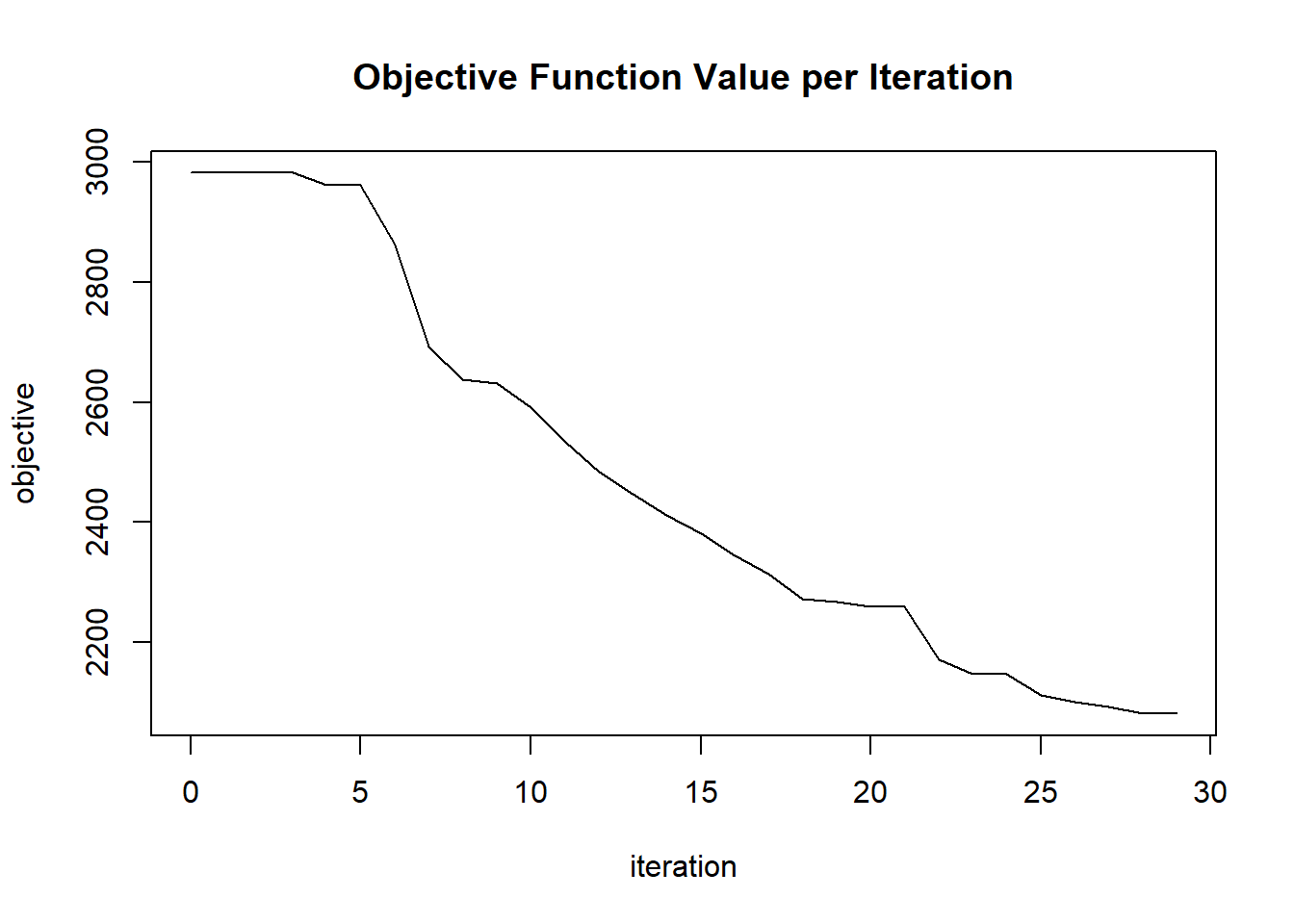
## Iteration 34 of 75 45.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 130 3 Quadratic L1 1 1 NA NA
## objective
## 130 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_67
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.03451 2144.58357
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1309.475
## Misclassification Error (Categorical): 355
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:00 0.011 sec 0 1.05000 2507.76069
## 2 2020-06-20 06:43:00 0.014 sec 1 0.70000 2507.76069
## 3 2020-06-20 06:43:00 0.015 sec 2 0.46667 2507.76069
## 4 2020-06-20 06:43:00 0.017 sec 3 0.31111 2507.76069
## 5 2020-06-20 06:43:00 0.018 sec 4 0.15556 2507.76069
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:00 0.044 sec 24 0.04259 2151.73251
## 26 2020-06-20 06:43:00 0.045 sec 25 0.04472 2150.28010
## 27 2020-06-20 06:43:00 0.047 sec 26 0.02981 2150.28010
## 28 2020-06-20 06:43:00 0.048 sec 27 0.03130 2146.31653
## 29 2020-06-20 06:43:00 0.049 sec 28 0.03287 2144.61249
## 30 2020-06-20 06:43:00 0.050 sec 29 0.03451 2144.58357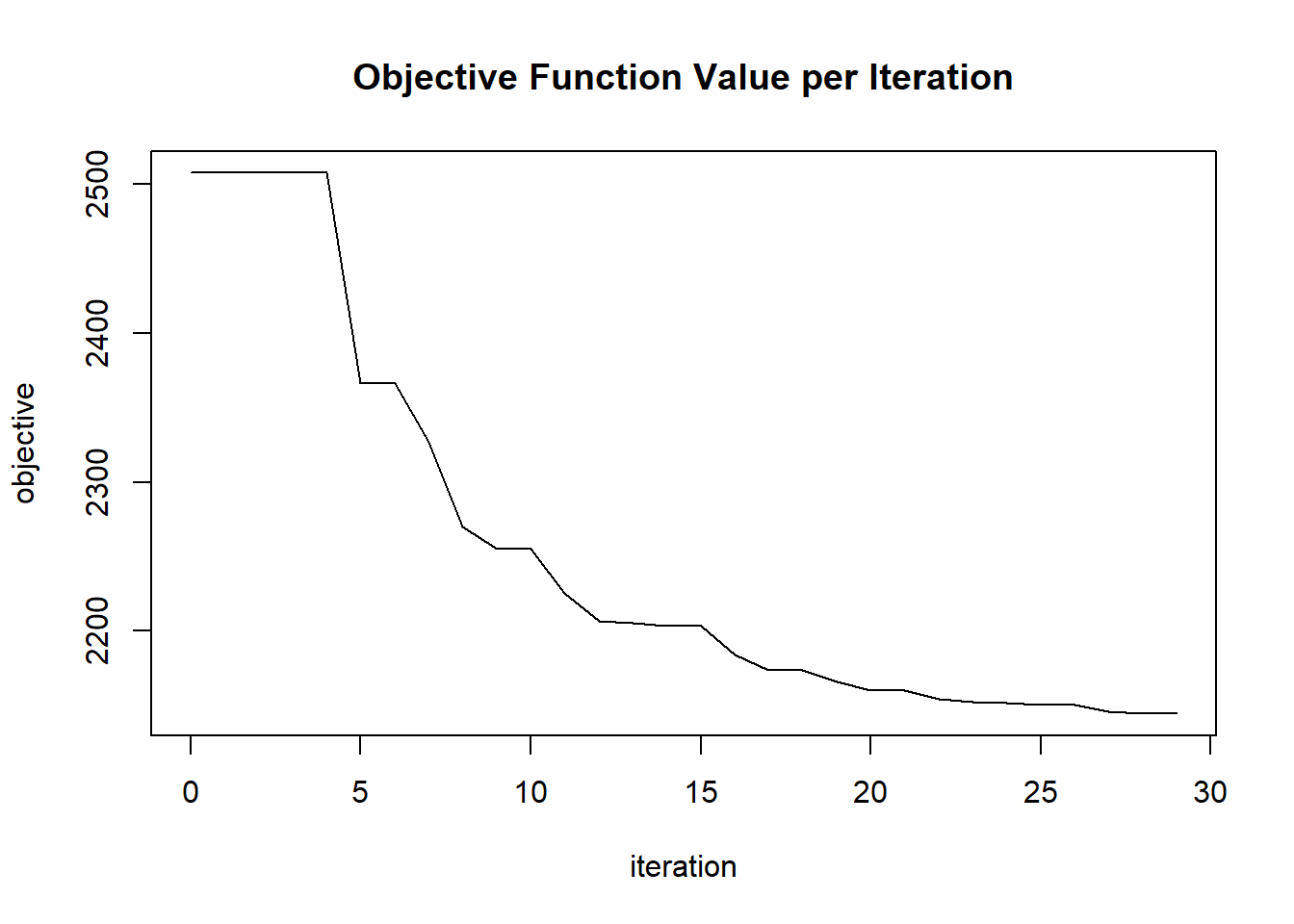
## Iteration 35 of 75 46.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 239 5 Quadratic L1 4 4 NA NA
## objective
## 239 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_69
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 2150.41754
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1418.276
## Misclassification Error (Categorical): 182
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:01 0.013 sec 0 1.05000 3424.98736
## 2 2020-06-20 06:43:01 0.015 sec 1 0.70000 3424.98736
## 3 2020-06-20 06:43:01 0.017 sec 2 0.46667 3424.98736
## 4 2020-06-20 06:43:01 0.019 sec 3 0.49000 3119.46329
## 5 2020-06-20 06:43:01 0.021 sec 4 0.51450 2777.96462
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:01 0.057 sec 24 0.08943 2191.26957
## 26 2020-06-20 06:43:01 0.059 sec 25 0.09390 2177.51025
## 27 2020-06-20 06:43:01 0.061 sec 26 0.09860 2173.64380
## 28 2020-06-20 06:43:01 0.062 sec 27 0.06573 2173.64380
## 29 2020-06-20 06:43:01 0.065 sec 28 0.06902 2157.48169
## 30 2020-06-20 06:43:01 0.066 sec 29 0.07247 2150.41754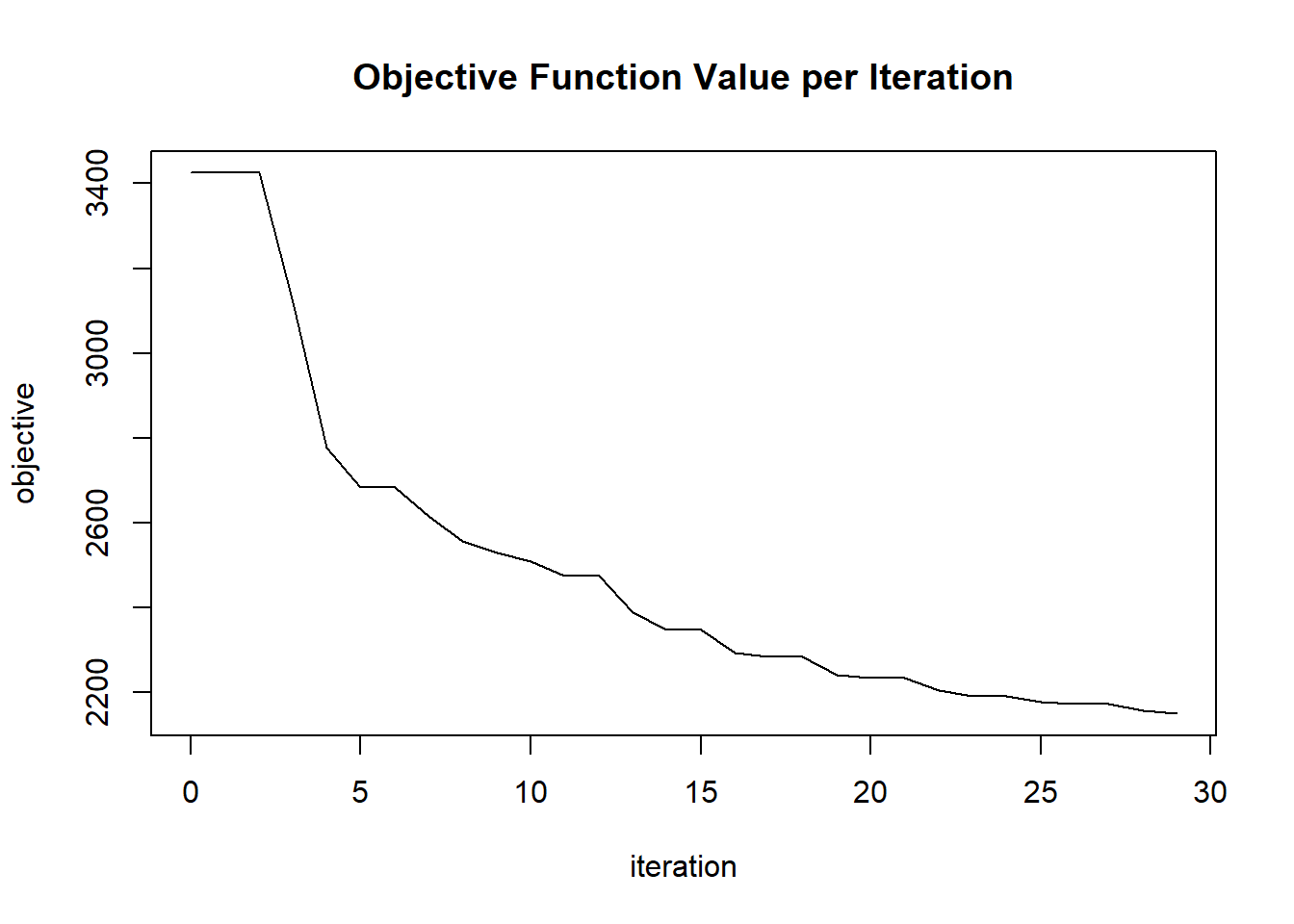
## Iteration 36 of 75 48%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 122 5 Quadratic Quadratic 1 1 NA NA
## objective
## 122 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_71
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.11414 1519.78355
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1367.928
## Misclassification Error (Categorical): 131
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:03 0.013 sec 0 1.05000 2578.38703
## 2 2020-06-20 06:43:03 0.015 sec 1 0.70000 2578.38703
## 3 2020-06-20 06:43:03 0.017 sec 2 0.46667 2578.38703
## 4 2020-06-20 06:43:03 0.019 sec 3 0.31111 2578.38703
## 5 2020-06-20 06:43:03 0.021 sec 4 0.32667 2487.60230
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:03 0.056 sec 24 0.14085 1552.31347
## 26 2020-06-20 06:43:03 0.057 sec 25 0.14790 1537.57691
## 27 2020-06-20 06:43:03 0.060 sec 26 0.15529 1533.90654
## 28 2020-06-20 06:43:03 0.062 sec 27 0.10353 1533.90654
## 29 2020-06-20 06:43:03 0.064 sec 28 0.10870 1523.88772
## 30 2020-06-20 06:43:03 0.066 sec 29 0.11414 1519.78355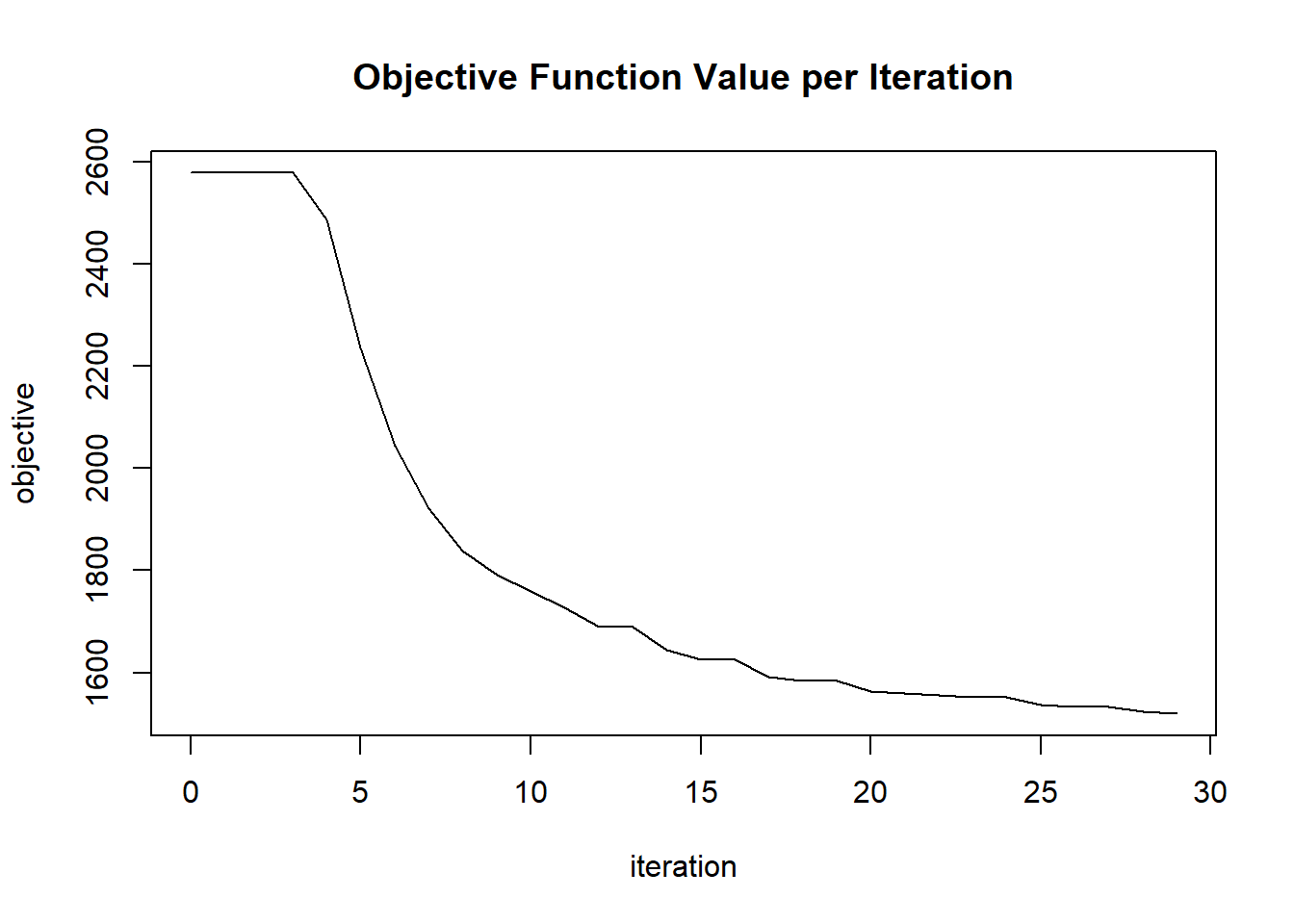
## Iteration 37 of 75 49.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 173 5 None Quadratic 0 4 NA NA
## objective
## 173 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_73
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 1482.29270
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1315.92
## Misclassification Error (Categorical): 171
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:05 0.012 sec 0 1.05000 3068.42772
## 2 2020-06-20 06:43:05 0.014 sec 1 0.70000 3068.42772
## 3 2020-06-20 06:43:05 0.016 sec 2 0.46667 3068.42772
## 4 2020-06-20 06:43:05 0.017 sec 3 0.49000 2854.74914
## 5 2020-06-20 06:43:05 0.019 sec 4 0.51450 2560.31423
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:05 0.053 sec 24 0.08943 1517.47774
## 26 2020-06-20 06:43:05 0.055 sec 25 0.09390 1502.84588
## 27 2020-06-20 06:43:05 0.057 sec 26 0.09860 1502.19339
## 28 2020-06-20 06:43:05 0.059 sec 27 0.06573 1502.19339
## 29 2020-06-20 06:43:05 0.061 sec 28 0.06902 1491.27720
## 30 2020-06-20 06:43:05 0.063 sec 29 0.07247 1482.29270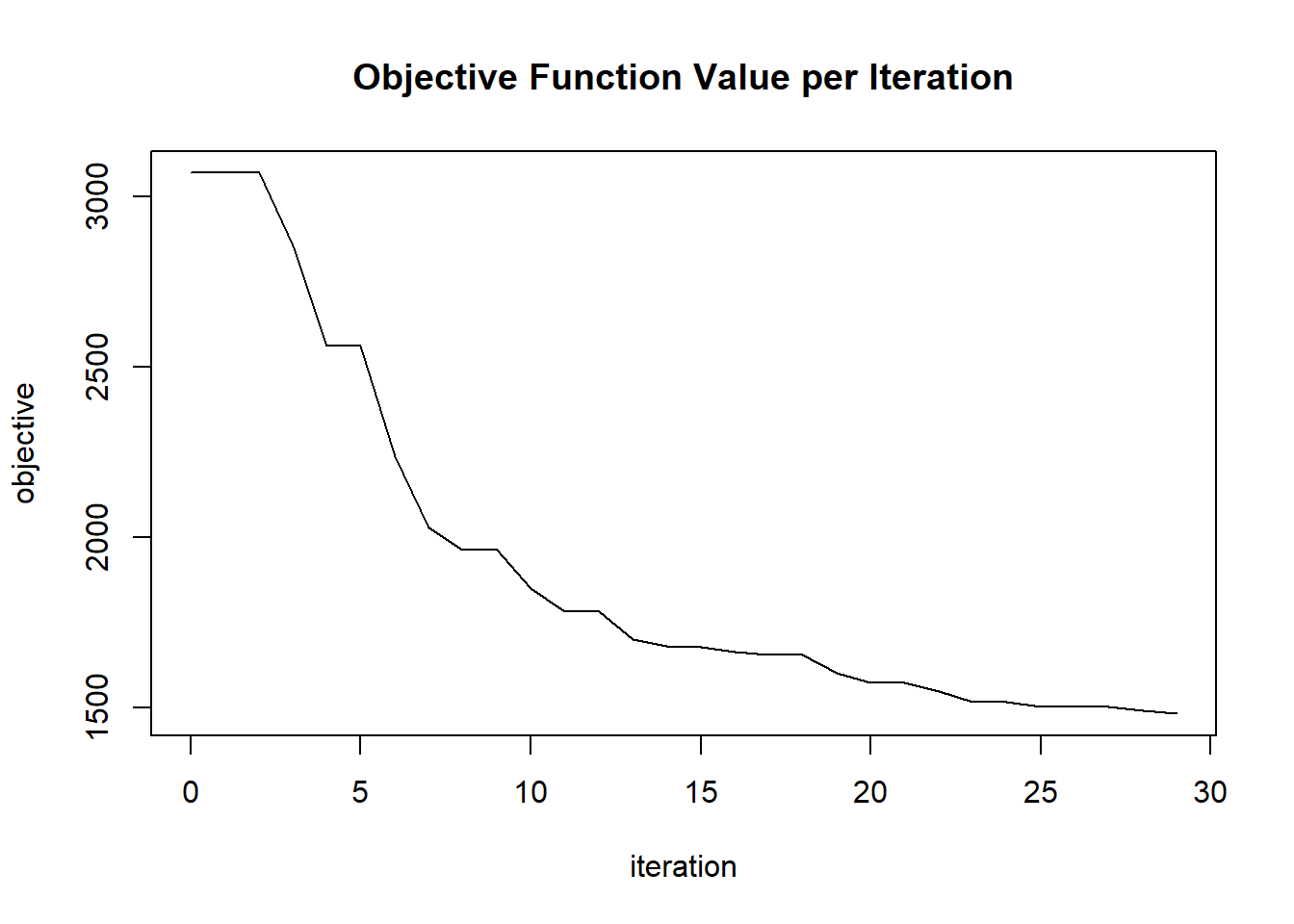
## Iteration 38 of 75 50.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 203 5 Quadratic Quadratic 1 4 NA NA
## objective
## 203 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_75
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 1930.70517
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1336.887
## Misclassification Error (Categorical): 180
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:06 0.012 sec 0 1.05000 3127.22747
## 2 2020-06-20 06:43:06 0.014 sec 1 0.70000 3127.22747
## 3 2020-06-20 06:43:06 0.015 sec 2 0.46667 3127.22747
## 4 2020-06-20 06:43:06 0.017 sec 3 0.49000 2834.07759
## 5 2020-06-20 06:43:06 0.019 sec 4 0.51450 2563.72728
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:06 0.054 sec 24 0.08943 1944.44926
## 26 2020-06-20 06:43:06 0.056 sec 25 0.09390 1942.43988
## 27 2020-06-20 06:43:06 0.058 sec 26 0.06260 1942.43988
## 28 2020-06-20 06:43:06 0.060 sec 27 0.06573 1933.84493
## 29 2020-06-20 06:43:06 0.061 sec 28 0.06902 1930.70517
## 30 2020-06-20 06:43:06 0.064 sec 29 0.04601 1930.70517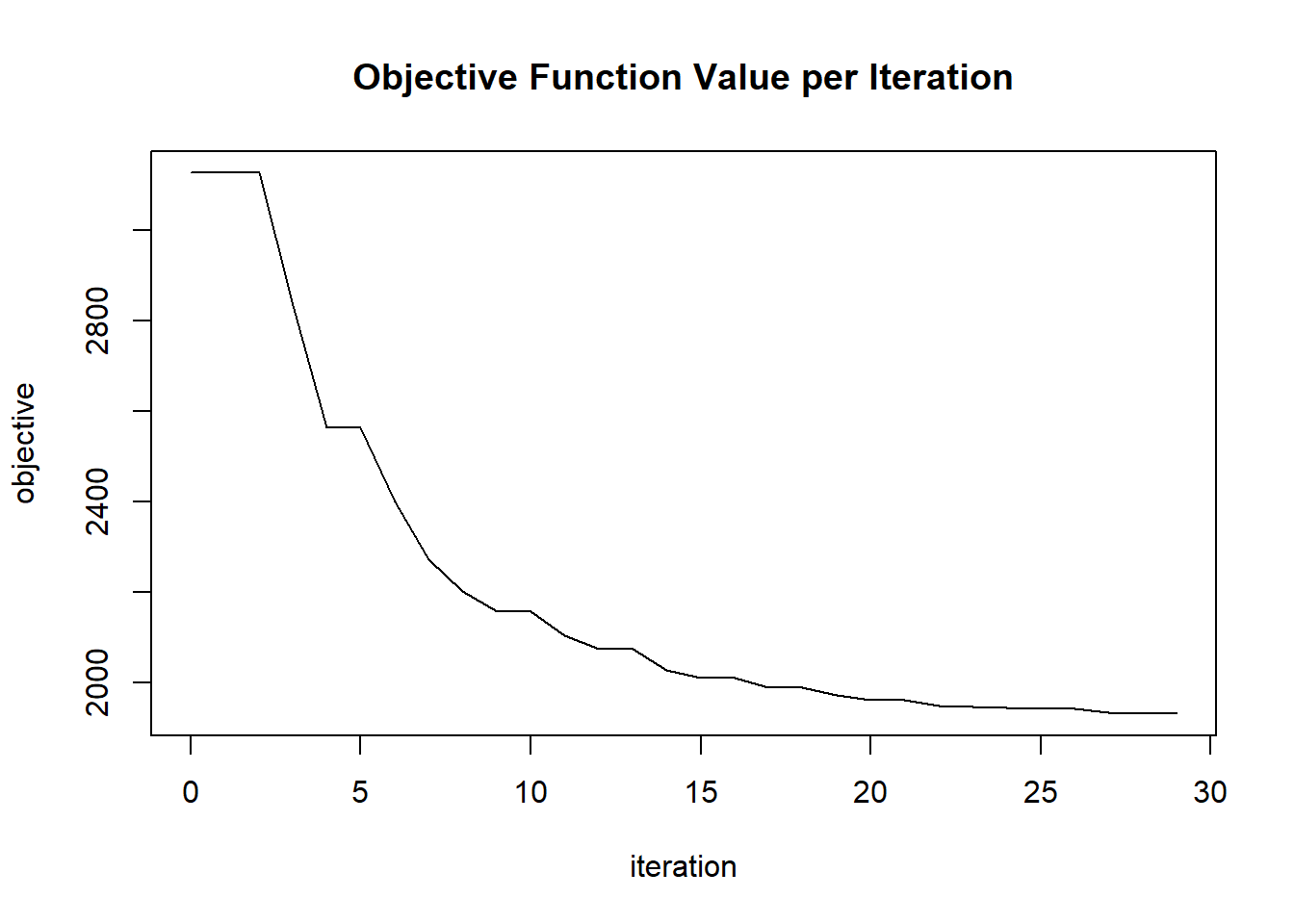
## Iteration 39 of 75 52%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 242 5 L1 L1 4 4 NA NA
## objective
## 242 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_77
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 2948.45252
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1598.26
## Misclassification Error (Categorical): 329
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:08 0.014 sec 0 1.05000 4795.71371
## 2 2020-06-20 06:43:08 0.015 sec 1 1.10250 4500.79254
## 3 2020-06-20 06:43:08 0.018 sec 2 0.73500 4500.79254
## 4 2020-06-20 06:43:08 0.020 sec 3 0.49000 4500.79254
## 5 2020-06-20 06:43:08 0.022 sec 4 0.32667 4500.79254
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:08 0.059 sec 24 0.08943 2989.19156
## 26 2020-06-20 06:43:08 0.060 sec 25 0.09390 2977.92552
## 27 2020-06-20 06:43:08 0.062 sec 26 0.09860 2964.77079
## 28 2020-06-20 06:43:08 0.064 sec 27 0.06573 2964.77079
## 29 2020-06-20 06:43:08 0.065 sec 28 0.06902 2951.99986
## 30 2020-06-20 06:43:08 0.067 sec 29 0.07247 2948.45252
## Iteration 40 of 75 53.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 206 5 L1 Quadratic 1 4 NA NA
## objective
## 206 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_79
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 2079.36189
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1322.782
## Misclassification Error (Categorical): 183
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:10 0.012 sec 0 1.05000 3341.70576
## 2 2020-06-20 06:43:10 0.014 sec 1 0.70000 3341.70576
## 3 2020-06-20 06:43:10 0.017 sec 2 0.46667 3341.70576
## 4 2020-06-20 06:43:10 0.019 sec 3 0.49000 3024.51256
## 5 2020-06-20 06:43:10 0.021 sec 4 0.51450 2971.00044
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:10 0.058 sec 24 0.05678 2100.15858
## 26 2020-06-20 06:43:10 0.059 sec 25 0.05962 2094.53229
## 27 2020-06-20 06:43:10 0.061 sec 26 0.06260 2090.51660
## 28 2020-06-20 06:43:10 0.063 sec 27 0.04173 2090.51660
## 29 2020-06-20 06:43:10 0.064 sec 28 0.04382 2084.80422
## 30 2020-06-20 06:43:10 0.066 sec 29 0.04601 2079.36189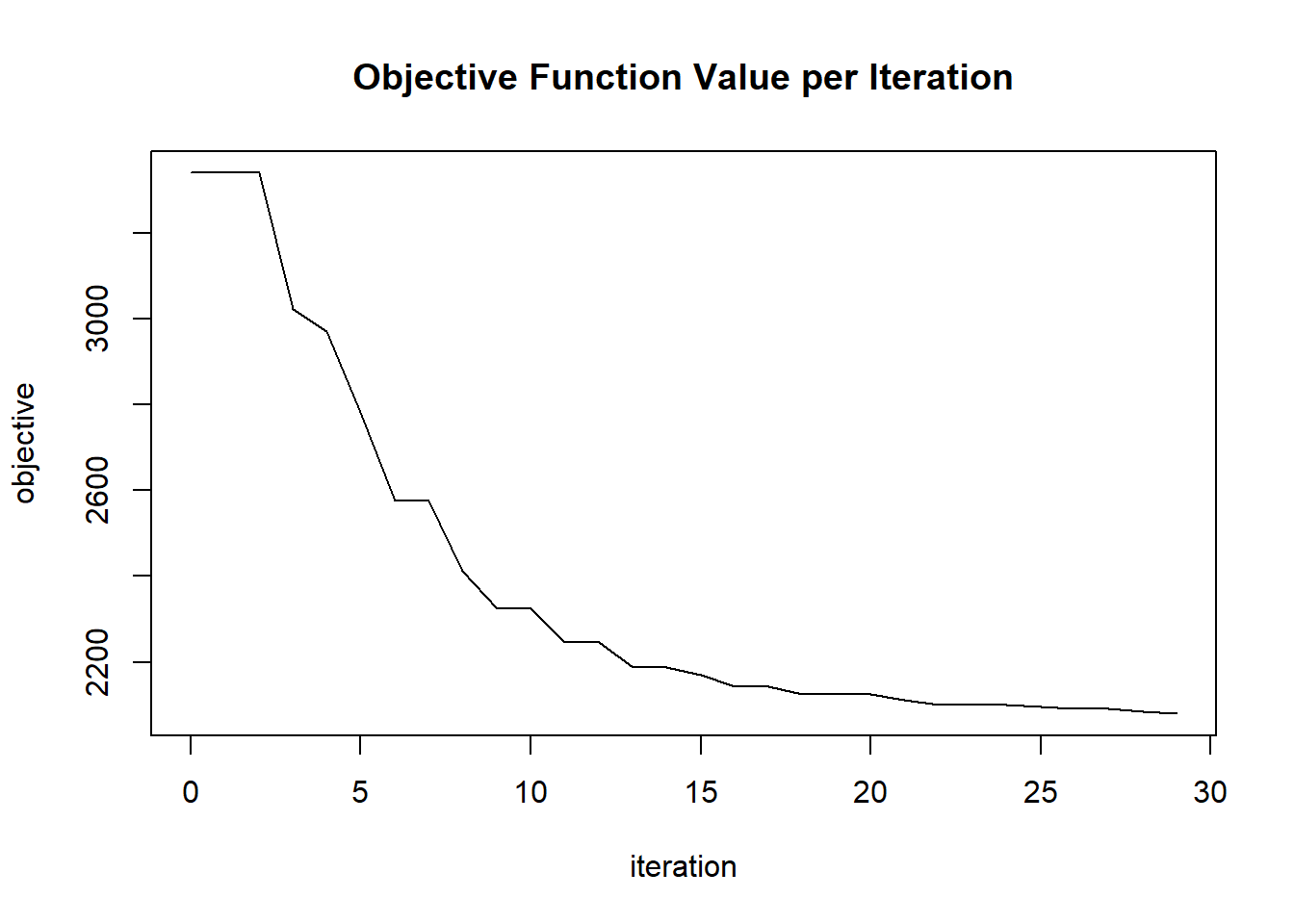
## Iteration 41 of 75 54.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 123 10 Quadratic Quadratic 1 1 NA NA
## objective
## 123 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_81
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 1084.67184
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 686.1051
## Misclassification Error (Categorical): 57
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:11 0.014 sec 0 1.05000 3095.07933
## 2 2020-06-20 06:43:11 0.017 sec 1 0.70000 3095.07933
## 3 2020-06-20 06:43:11 0.019 sec 2 0.46667 3095.07933
## 4 2020-06-20 06:43:11 0.022 sec 3 0.49000 2811.09144
## 5 2020-06-20 06:43:11 0.025 sec 4 0.51450 2443.56691
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:11 0.083 sec 24 0.22184 1101.55410
## 26 2020-06-20 06:43:11 0.086 sec 25 0.14790 1101.55410
## 27 2020-06-20 06:43:11 0.089 sec 26 0.15529 1089.21771
## 28 2020-06-20 06:43:11 0.092 sec 27 0.16306 1088.15959
## 29 2020-06-20 06:43:11 0.095 sec 28 0.17121 1087.68494
## 30 2020-06-20 06:43:11 0.098 sec 29 0.17977 1084.67184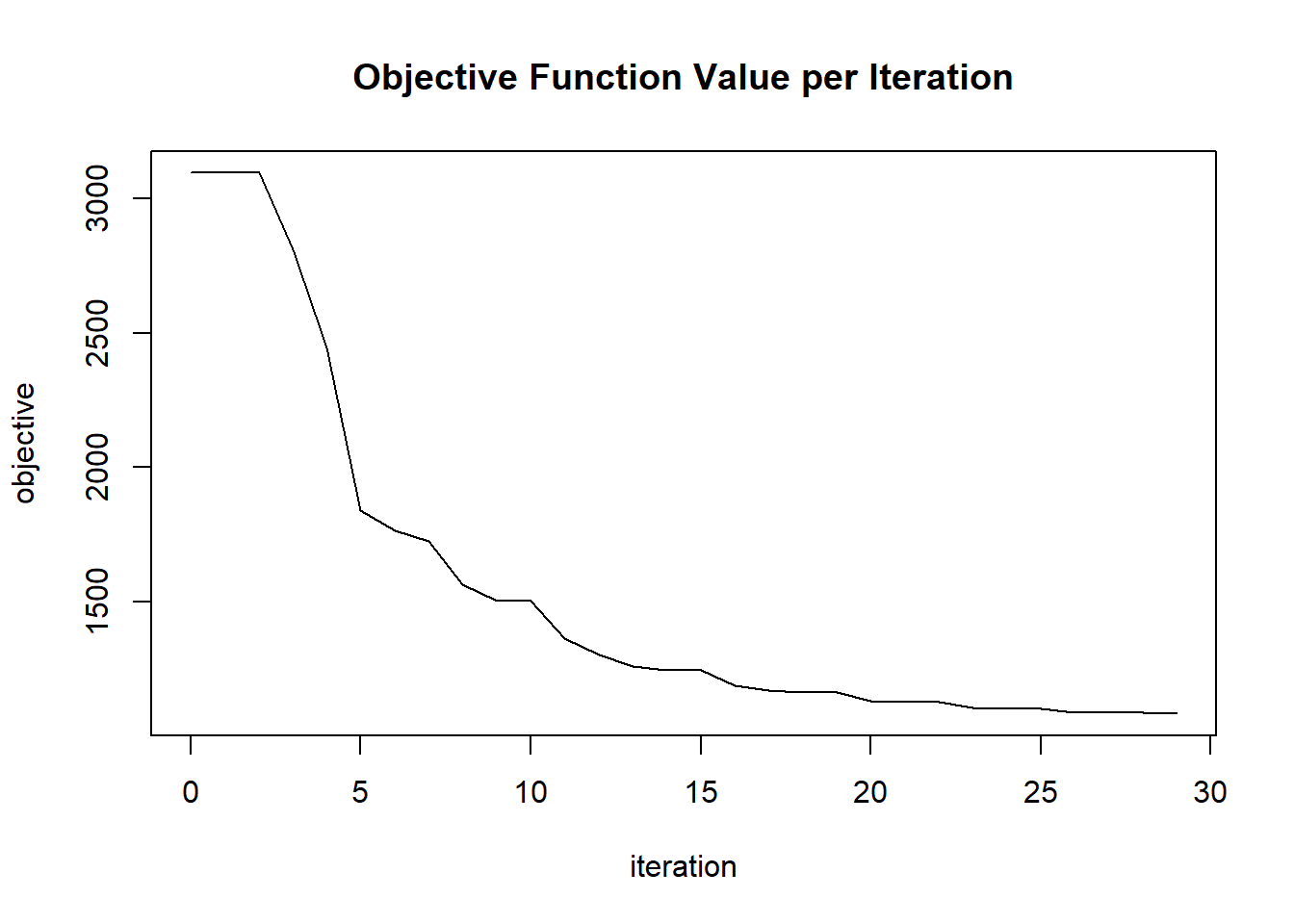
## Iteration 42 of 75 56%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 134 5 L1 L1 1 1 NA NA
## objective
## 134 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_83
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.33445 1744.83347
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1383.495
## Misclassification Error (Categorical): 133
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:13 0.010 sec 0 1.05000 2579.39882
## 2 2020-06-20 06:43:13 0.012 sec 1 0.70000 2579.39882
## 3 2020-06-20 06:43:13 0.013 sec 2 0.46667 2579.39882
## 4 2020-06-20 06:43:13 0.015 sec 3 0.31111 2579.39882
## 5 2020-06-20 06:43:13 0.017 sec 4 0.15556 2579.39882
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:13 0.050 sec 24 0.41274 1795.25220
## 26 2020-06-20 06:43:13 0.052 sec 25 0.43337 1769.02348
## 27 2020-06-20 06:43:13 0.054 sec 26 0.45504 1758.16588
## 28 2020-06-20 06:43:13 0.056 sec 27 0.47779 1753.70096
## 29 2020-06-20 06:43:13 0.057 sec 28 0.50168 1744.83347
## 30 2020-06-20 06:43:13 0.059 sec 29 0.33445 1744.83347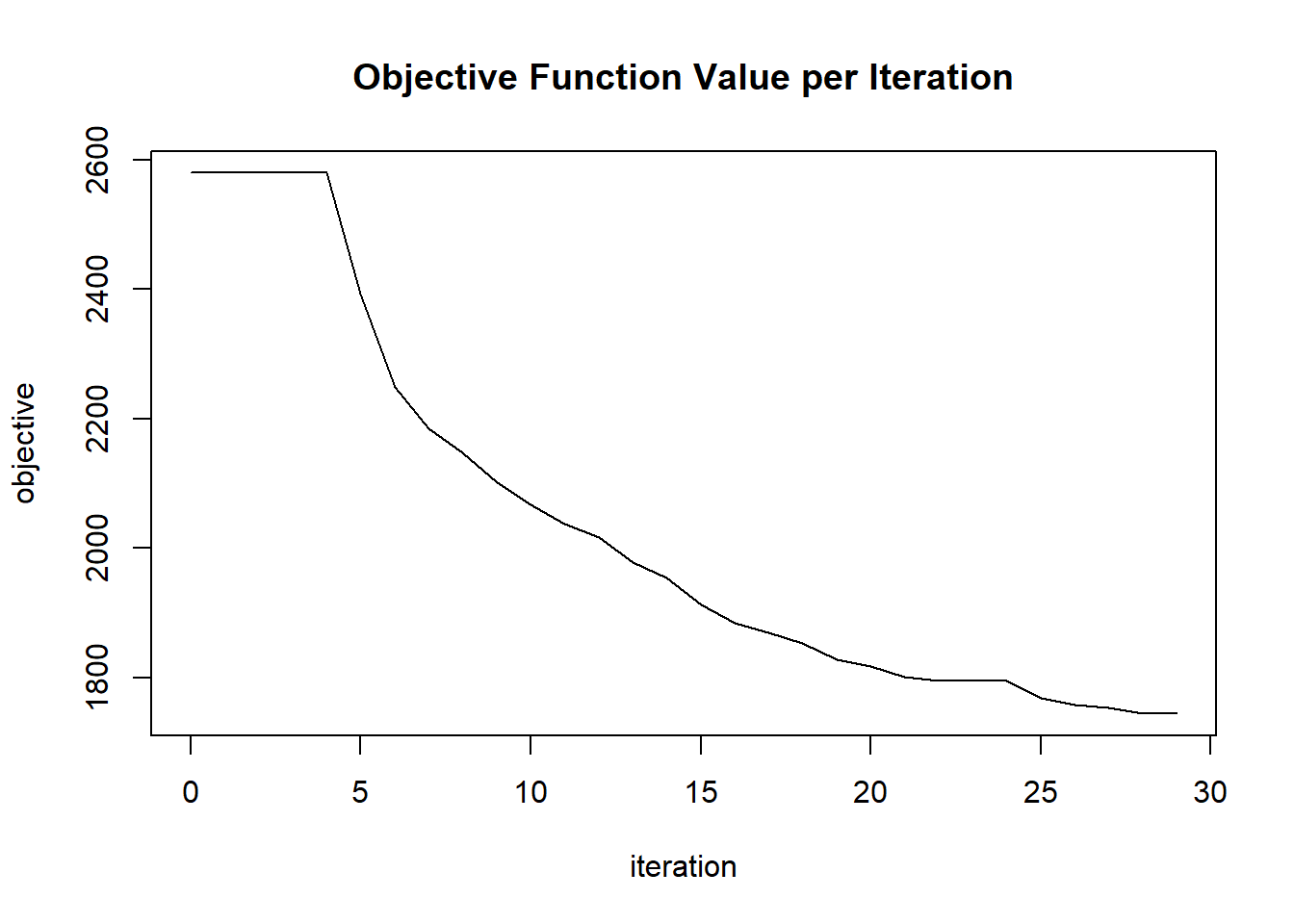
## Iteration 43 of 75 57.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 238 3 Quadratic L1 4 4 NA NA
## objective
## 238 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_85
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.02921 2652.58179
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1462.412
## Misclassification Error (Categorical): 354
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:15 0.010 sec 0 1.05000 3118.13658
## 2 2020-06-20 06:43:15 0.012 sec 1 0.70000 3118.13658
## 3 2020-06-20 06:43:15 0.013 sec 2 0.46667 3118.13658
## 4 2020-06-20 06:43:15 0.014 sec 3 0.31111 3118.13658
## 5 2020-06-20 06:43:15 0.015 sec 4 0.32667 3040.31848
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:15 0.045 sec 24 0.03605 2657.57725
## 26 2020-06-20 06:43:15 0.047 sec 25 0.03785 2655.80855
## 27 2020-06-20 06:43:15 0.049 sec 26 0.02524 2655.80855
## 28 2020-06-20 06:43:15 0.050 sec 27 0.02650 2653.69713
## 29 2020-06-20 06:43:15 0.051 sec 28 0.02782 2652.81054
## 30 2020-06-20 06:43:15 0.053 sec 29 0.02921 2652.58179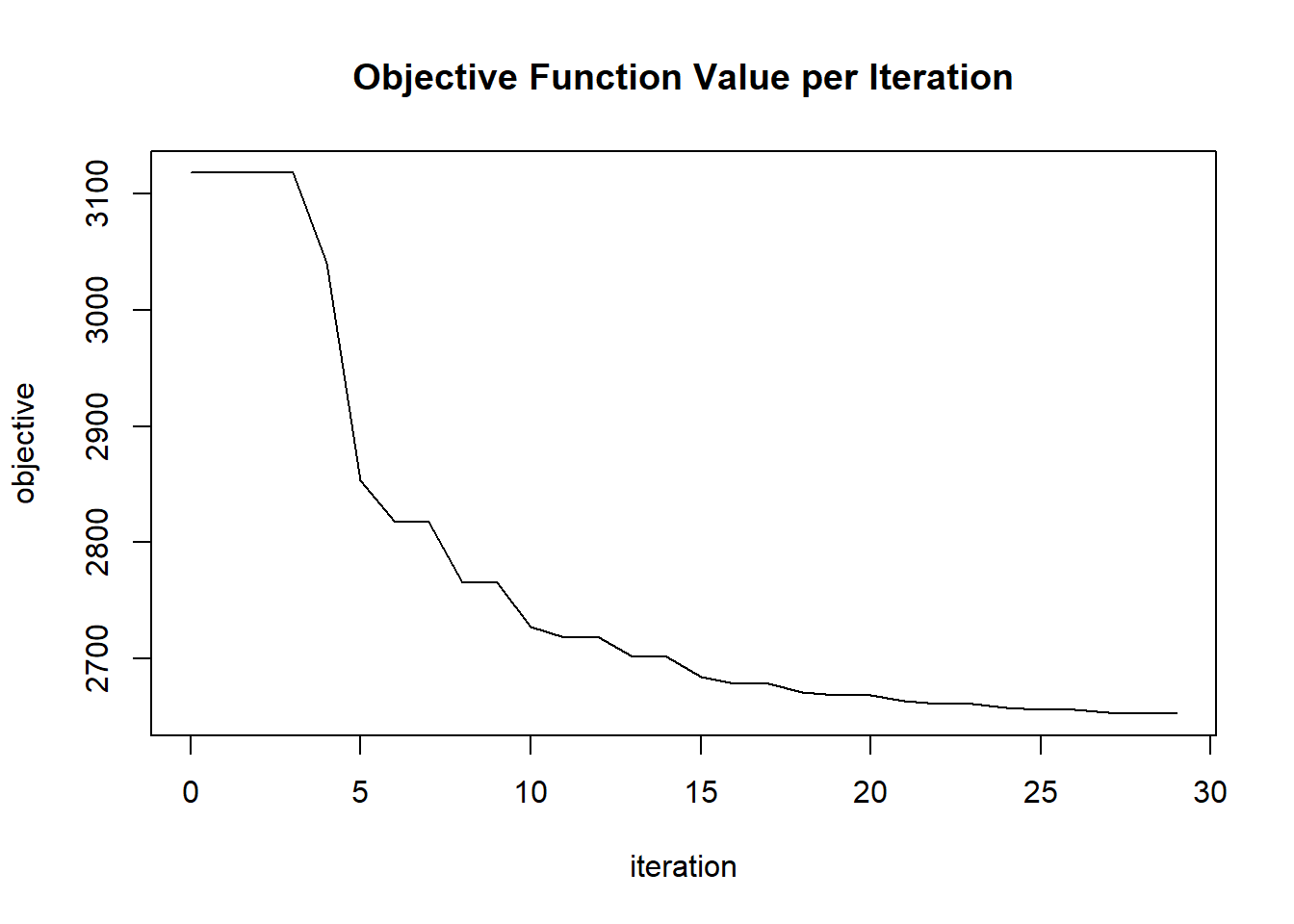
## Iteration 44 of 75 58.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 2 5 None None 0 0 NA NA
## objective
## 2 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_87
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.33445 1014.94643
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1402.818
## Misclassification Error (Categorical): 99
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:16 0.010 sec 0 1.05000 2185.59449
## 2 2020-06-20 06:43:16 0.012 sec 1 0.70000 2185.59449
## 3 2020-06-20 06:43:16 0.013 sec 2 0.46667 2185.59449
## 4 2020-06-20 06:43:16 0.015 sec 3 0.31111 2185.59449
## 5 2020-06-20 06:43:16 0.016 sec 4 0.15556 2185.59449
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:16 0.051 sec 24 0.41274 1152.19526
## 26 2020-06-20 06:43:16 0.053 sec 25 0.43337 1132.70939
## 27 2020-06-20 06:43:16 0.054 sec 26 0.45504 1088.30737
## 28 2020-06-20 06:43:16 0.056 sec 27 0.30336 1088.30737
## 29 2020-06-20 06:43:16 0.058 sec 28 0.31853 1047.81879
## 30 2020-06-20 06:43:16 0.060 sec 29 0.33445 1014.94643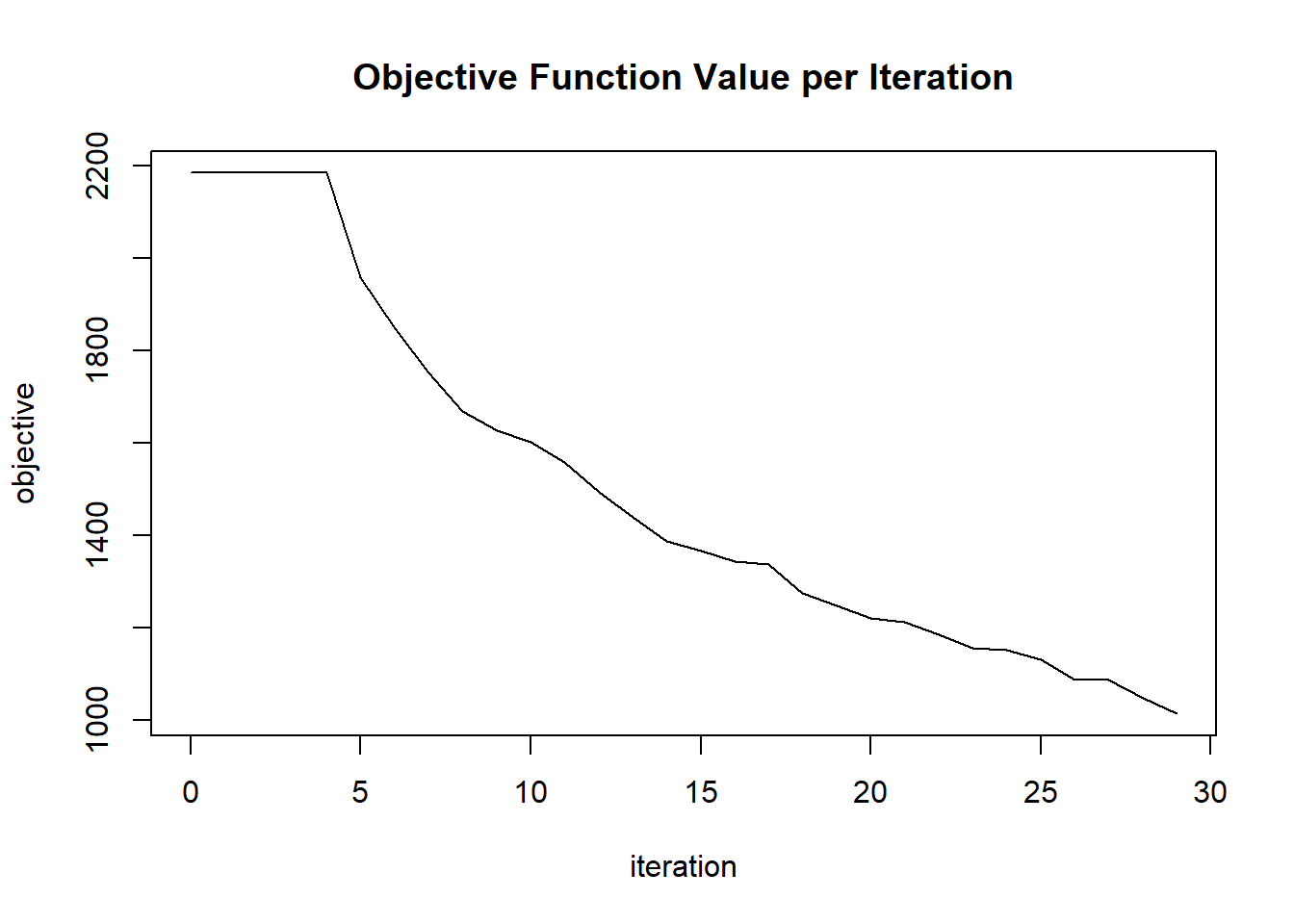
## Iteration 45 of 75 60%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 61 3 L1 None 4 0 NA NA
## objective
## 61 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_89
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.02921 2426.38448
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1437.937
## Misclassification Error (Categorical): 356
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:18 0.007 sec 0 1.05000 4013.30781
## 2 2020-06-20 06:43:18 0.008 sec 1 0.70000 4013.30781
## 3 2020-06-20 06:43:18 0.010 sec 2 0.46667 4013.30781
## 4 2020-06-20 06:43:18 0.011 sec 3 0.49000 3197.67079
## 5 2020-06-20 06:43:18 0.012 sec 4 0.51450 2968.36765
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:18 0.037 sec 24 0.05678 2449.40841
## 26 2020-06-20 06:43:18 0.039 sec 25 0.05962 2436.98627
## 27 2020-06-20 06:43:18 0.041 sec 26 0.03975 2436.98627
## 28 2020-06-20 06:43:18 0.042 sec 27 0.04173 2429.78051
## 29 2020-06-20 06:43:18 0.043 sec 28 0.04382 2426.38448
## 30 2020-06-20 06:43:18 0.045 sec 29 0.02921 2426.38448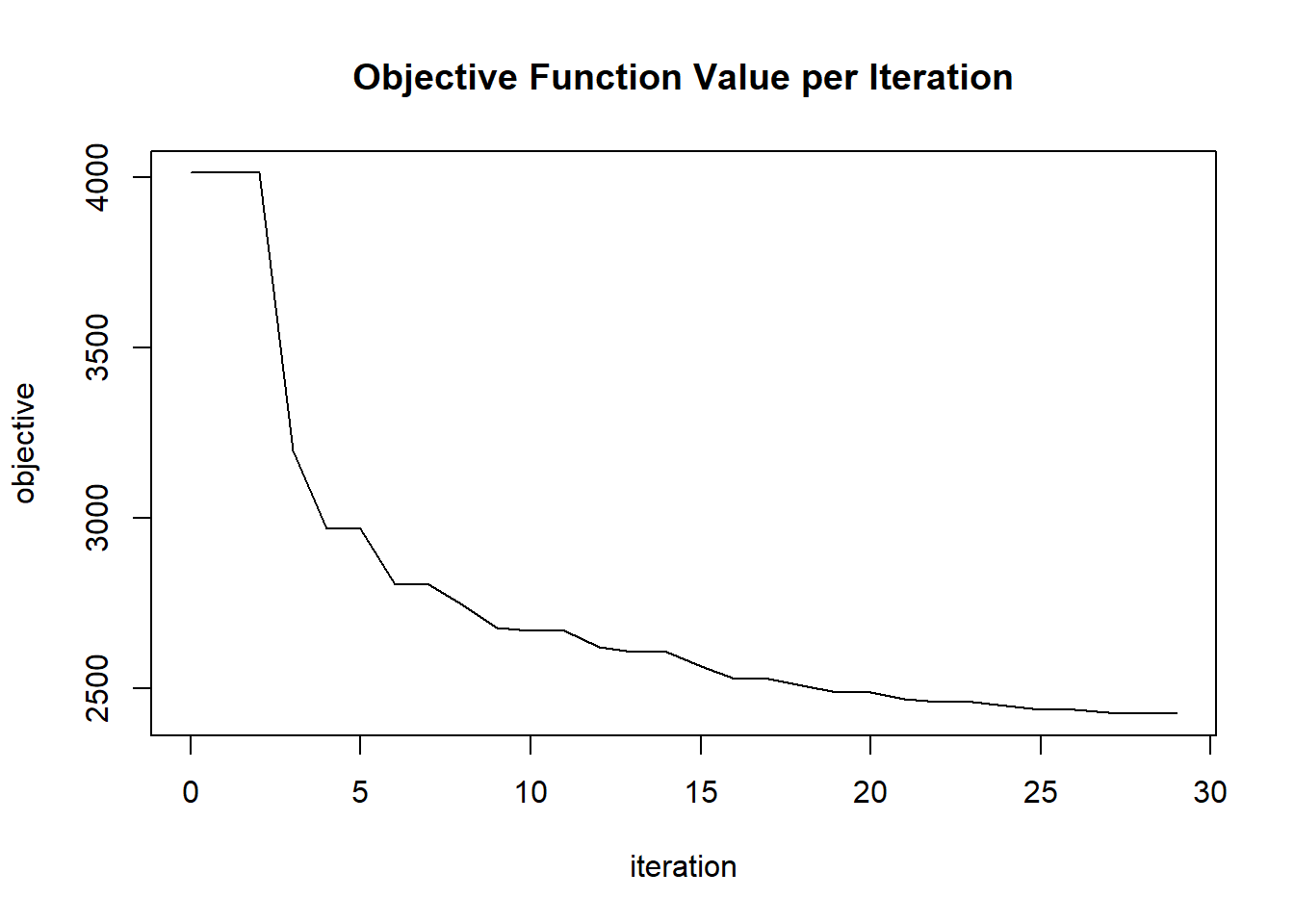
## Iteration 46 of 75 61.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 93 10 None Quadratic 0 1 NA NA
## objective
## 93 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_91
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.28314 673.15490
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 672.7126
## Misclassification Error (Categorical): 32
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:19 0.017 sec 0 1.05000 3579.80142
## 2 2020-06-20 06:43:19 0.020 sec 1 0.70000 3579.80142
## 3 2020-06-20 06:43:19 0.023 sec 2 0.46667 3579.80142
## 4 2020-06-20 06:43:19 0.027 sec 3 0.49000 3363.03916
## 5 2020-06-20 06:43:19 0.032 sec 4 0.51450 3321.38482
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:20 0.092 sec 24 0.22184 705.40792
## 26 2020-06-20 06:43:20 0.095 sec 25 0.23294 688.41365
## 27 2020-06-20 06:43:20 0.100 sec 26 0.24458 682.69714
## 28 2020-06-20 06:43:20 0.104 sec 27 0.25681 676.12303
## 29 2020-06-20 06:43:20 0.107 sec 28 0.26965 673.83462
## 30 2020-06-20 06:43:20 0.110 sec 29 0.28314 673.15490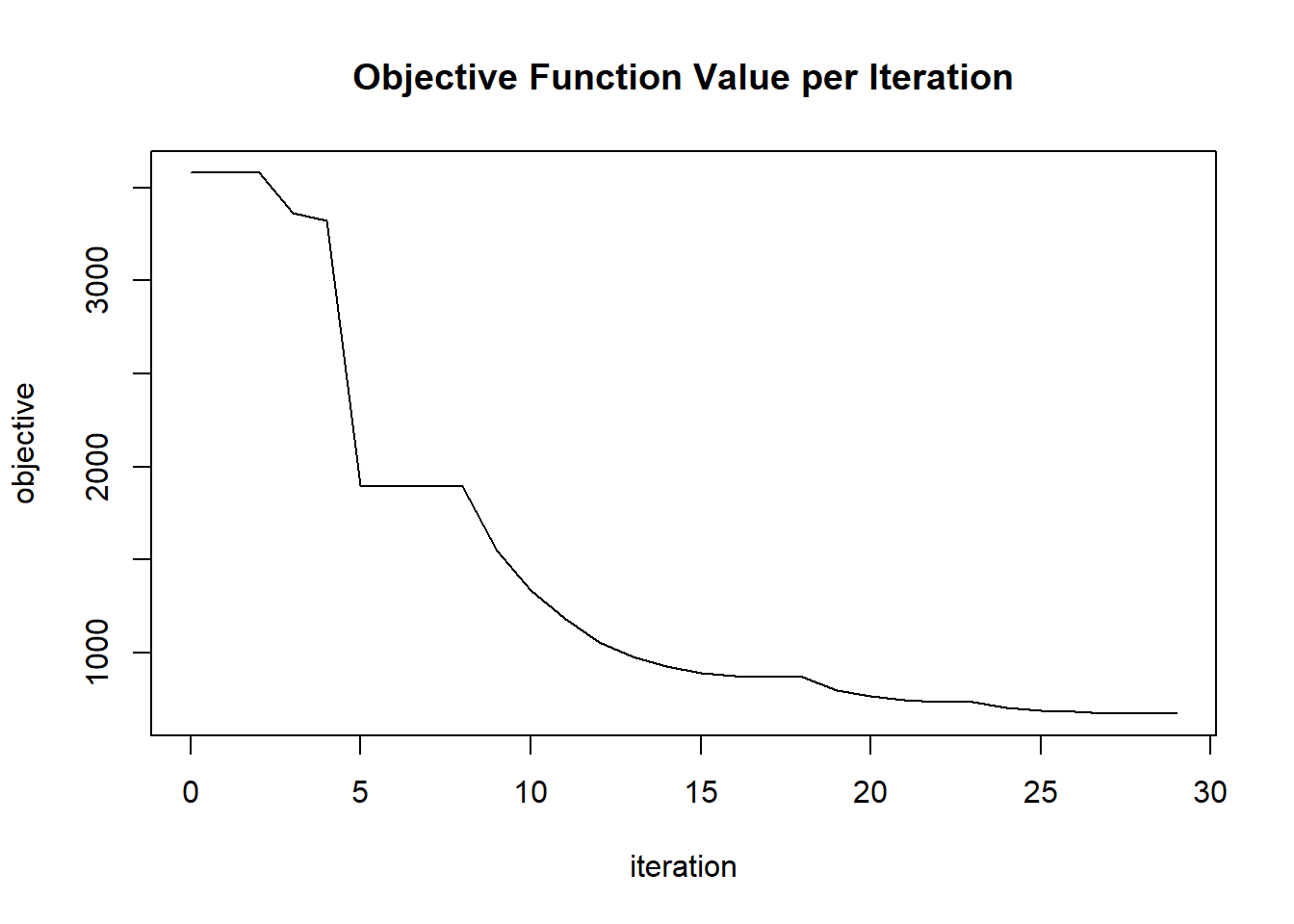
## Iteration 47 of 75 62.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 121 3 Quadratic Quadratic 1 1 NA NA
## objective
## 121 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_93
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.21235 2150.62414
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1465.875
## Misclassification Error (Categorical): 312
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:21 0.008 sec 0 1.05000 2667.68481
## 2 2020-06-20 06:43:21 0.009 sec 1 0.70000 2667.68481
## 3 2020-06-20 06:43:21 0.011 sec 2 0.46667 2667.68481
## 4 2020-06-20 06:43:21 0.012 sec 3 0.31111 2667.68481
## 5 2020-06-20 06:43:21 0.013 sec 4 0.15556 2667.68481
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:21 0.037 sec 24 0.41274 2199.89428
## 26 2020-06-20 06:43:21 0.038 sec 25 0.27516 2199.89428
## 27 2020-06-20 06:43:21 0.039 sec 26 0.28891 2162.57483
## 28 2020-06-20 06:43:21 0.040 sec 27 0.30336 2152.58807
## 29 2020-06-20 06:43:21 0.041 sec 28 0.31853 2150.62414
## 30 2020-06-20 06:43:21 0.043 sec 29 0.21235 2150.62414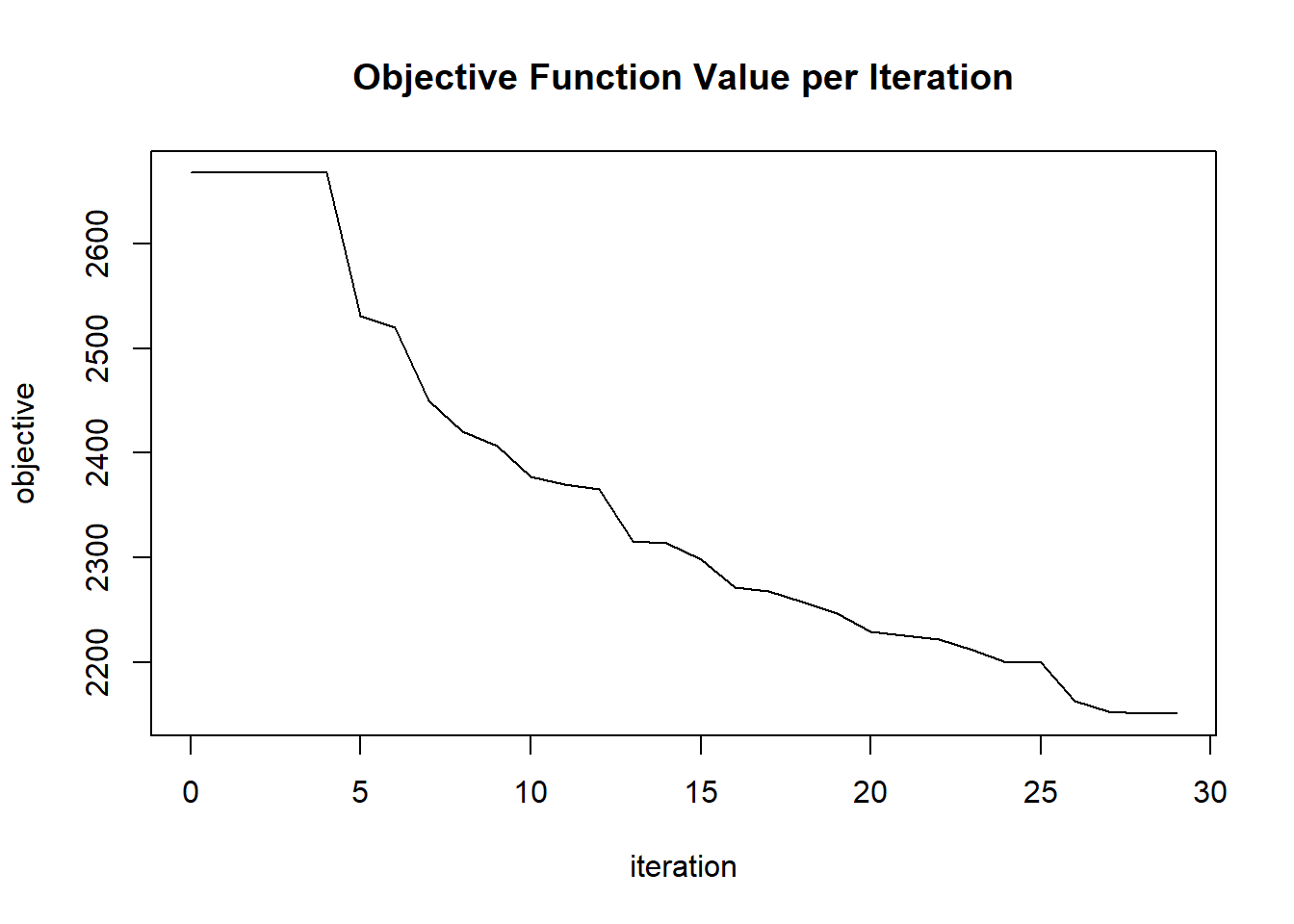
## Iteration 48 of 75 64%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 182 5 None L1 0 4 NA NA
## objective
## 182 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_95
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 1392.08683
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1408.063
## Misclassification Error (Categorical): 103
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:23 0.027 sec 0 1.05000 2916.36675
## 2 2020-06-20 06:43:23 0.029 sec 1 0.70000 2916.36675
## 3 2020-06-20 06:43:23 0.031 sec 2 0.46667 2916.36675
## 4 2020-06-20 06:43:23 0.033 sec 3 0.31111 2916.36675
## 5 2020-06-20 06:43:23 0.035 sec 4 0.32667 2791.12956
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:23 0.077 sec 24 0.22184 1443.36480
## 26 2020-06-20 06:43:23 0.079 sec 25 0.23294 1436.83073
## 27 2020-06-20 06:43:23 0.080 sec 26 0.15529 1436.83073
## 28 2020-06-20 06:43:23 0.082 sec 27 0.16306 1410.77093
## 29 2020-06-20 06:43:23 0.084 sec 28 0.17121 1395.47972
## 30 2020-06-20 06:43:23 0.085 sec 29 0.17977 1392.08683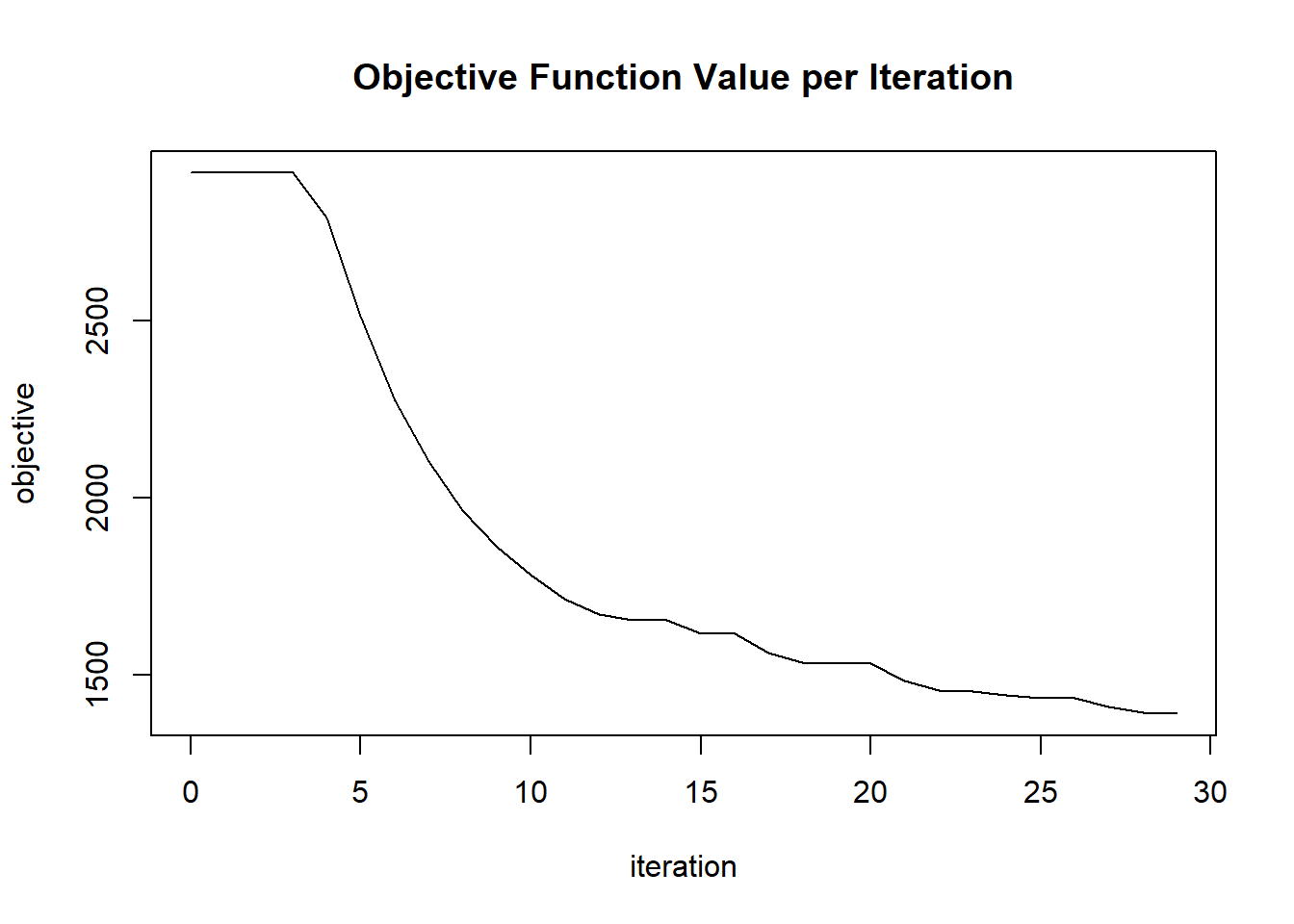
## Iteration 49 of 75 65.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 150 10 Quadratic Quadratic 4 1 NA NA
## objective
## 150 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_97
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 1609.31677
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 823.3452
## Misclassification Error (Categorical): 98
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:24 0.015 sec 0 1.05000 3100.81480
## 2 2020-06-20 06:43:24 0.018 sec 1 0.70000 3100.81480
## 3 2020-06-20 06:43:24 0.021 sec 2 0.46667 3100.81480
## 4 2020-06-20 06:43:24 0.024 sec 3 0.49000 2648.56823
## 5 2020-06-20 06:43:24 0.027 sec 4 0.51450 2342.02873
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:24 0.087 sec 24 0.08943 1641.91469
## 26 2020-06-20 06:43:24 0.090 sec 25 0.09390 1626.98175
## 27 2020-06-20 06:43:24 0.093 sec 26 0.09860 1623.70644
## 28 2020-06-20 06:43:24 0.096 sec 27 0.06573 1623.70644
## 29 2020-06-20 06:43:24 0.099 sec 28 0.06902 1611.96978
## 30 2020-06-20 06:43:24 0.102 sec 29 0.07247 1609.31677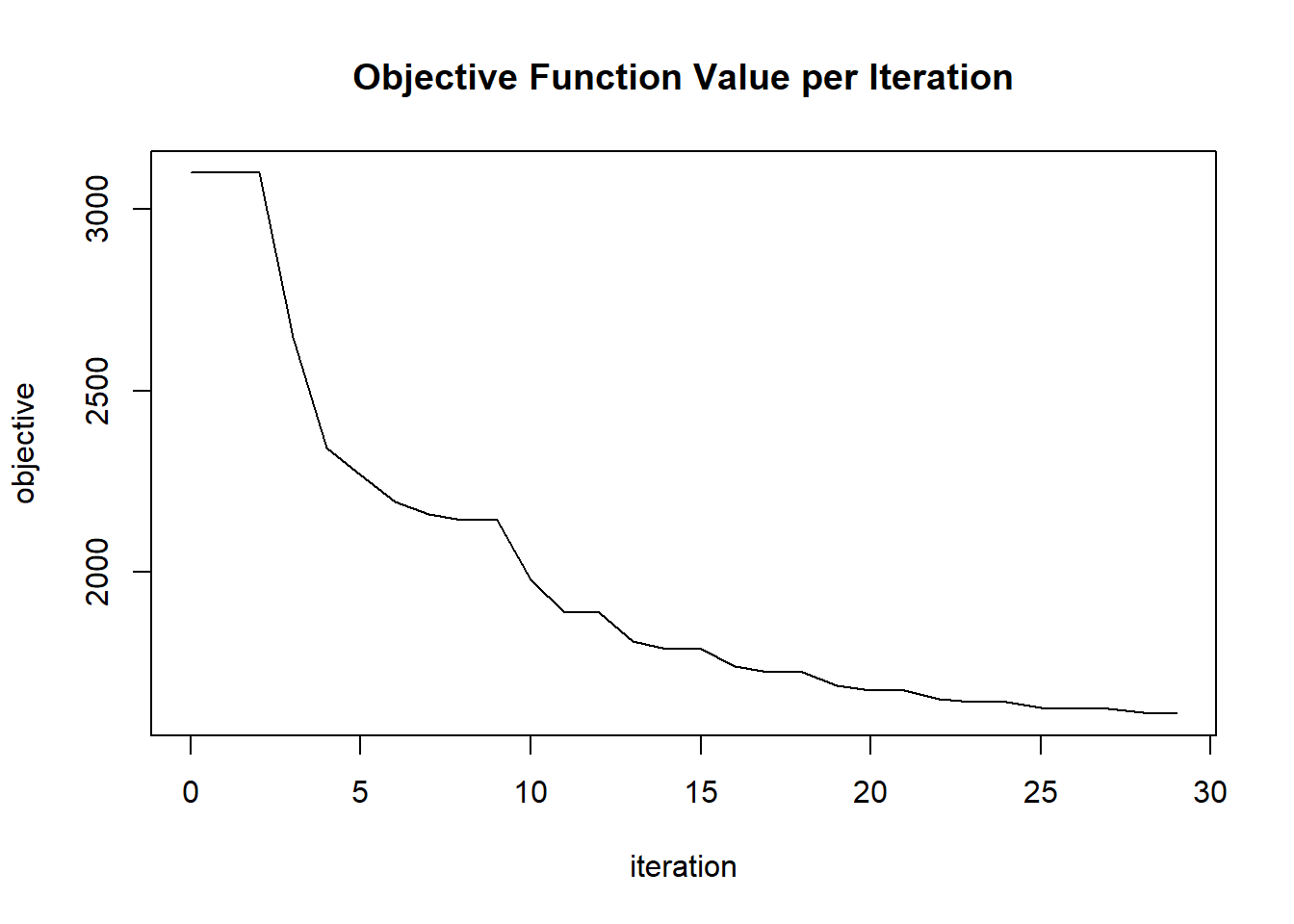
## Iteration 50 of 75 66.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 241 3 L1 L1 4 4 NA NA
## objective
## 241 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_99
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 2928.43078
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1647.195
## Misclassification Error (Categorical): 350
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:26 0.014 sec 0 1.05000 4487.86031
## 2 2020-06-20 06:43:26 0.016 sec 1 0.70000 4487.86031
## 3 2020-06-20 06:43:26 0.018 sec 2 0.73500 4051.87301
## 4 2020-06-20 06:43:26 0.020 sec 3 0.77175 3823.08667
## 5 2020-06-20 06:43:26 0.022 sec 4 0.51450 3823.08667
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:26 0.051 sec 24 0.08943 2968.04422
## 26 2020-06-20 06:43:26 0.053 sec 25 0.09390 2953.66584
## 27 2020-06-20 06:43:26 0.054 sec 26 0.09860 2944.82682
## 28 2020-06-20 06:43:26 0.055 sec 27 0.06573 2944.82682
## 29 2020-06-20 06:43:26 0.057 sec 28 0.06902 2934.64861
## 30 2020-06-20 06:43:26 0.058 sec 29 0.07247 2928.43078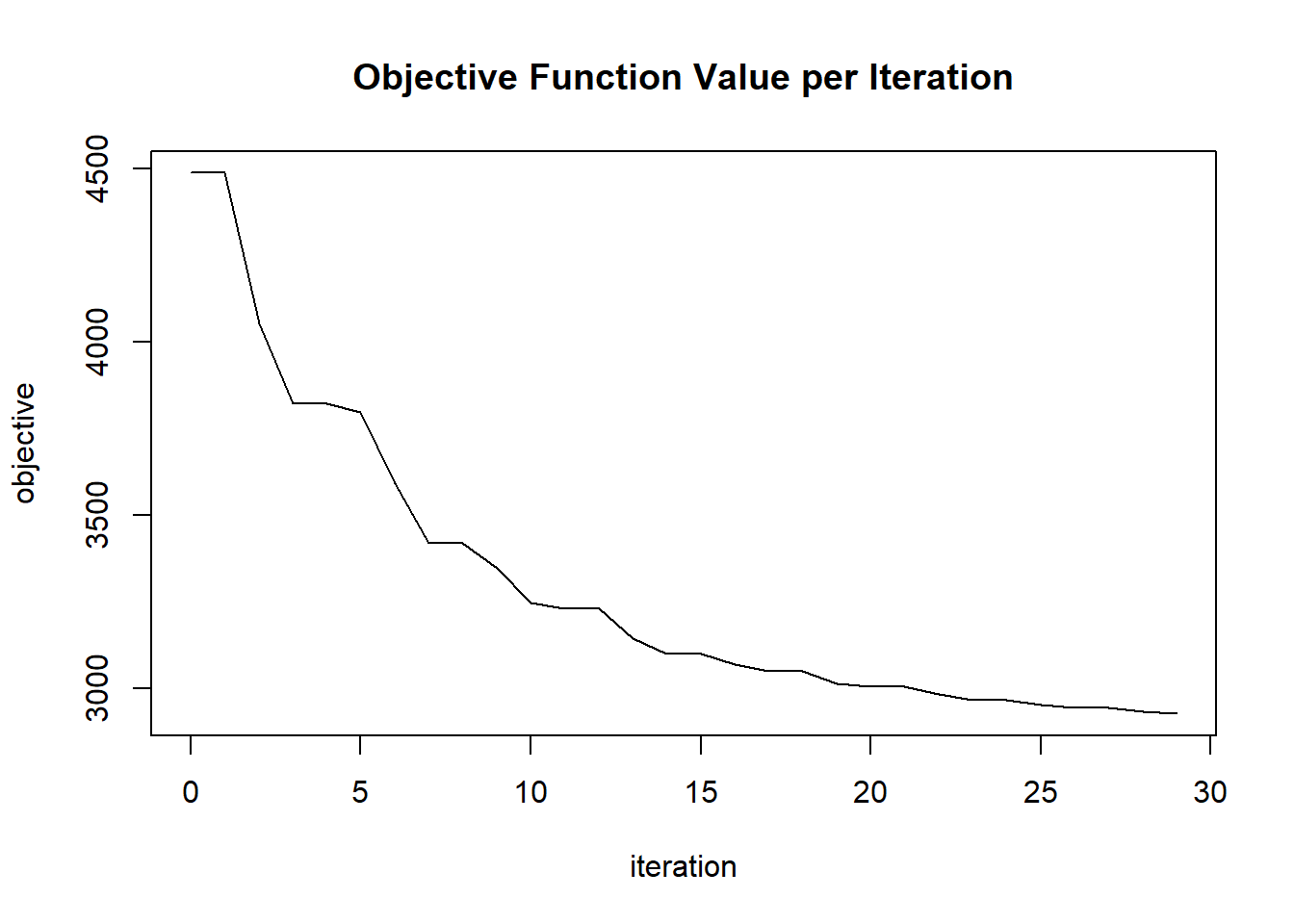
## Iteration 51 of 75 68%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 100 3 None L1 0 1 NA NA
## objective
## 100 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_101
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.05435 2035.61522
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1322.072
## Misclassification Error (Categorical): 306
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:28 0.009 sec 0 1.05000 2592.66352
## 2 2020-06-20 06:43:28 0.010 sec 1 0.70000 2592.66352
## 3 2020-06-20 06:43:28 0.012 sec 2 0.46667 2592.66352
## 4 2020-06-20 06:43:28 0.013 sec 3 0.31111 2592.66352
## 5 2020-06-20 06:43:28 0.014 sec 4 0.15556 2592.66352
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:28 0.037 sec 24 0.10564 2058.92754
## 26 2020-06-20 06:43:28 0.039 sec 25 0.07043 2058.92754
## 27 2020-06-20 06:43:28 0.040 sec 26 0.07395 2050.21618
## 28 2020-06-20 06:43:28 0.041 sec 27 0.07765 2043.15704
## 29 2020-06-20 06:43:28 0.042 sec 28 0.05176 2043.15704
## 30 2020-06-20 06:43:28 0.043 sec 29 0.05435 2035.61522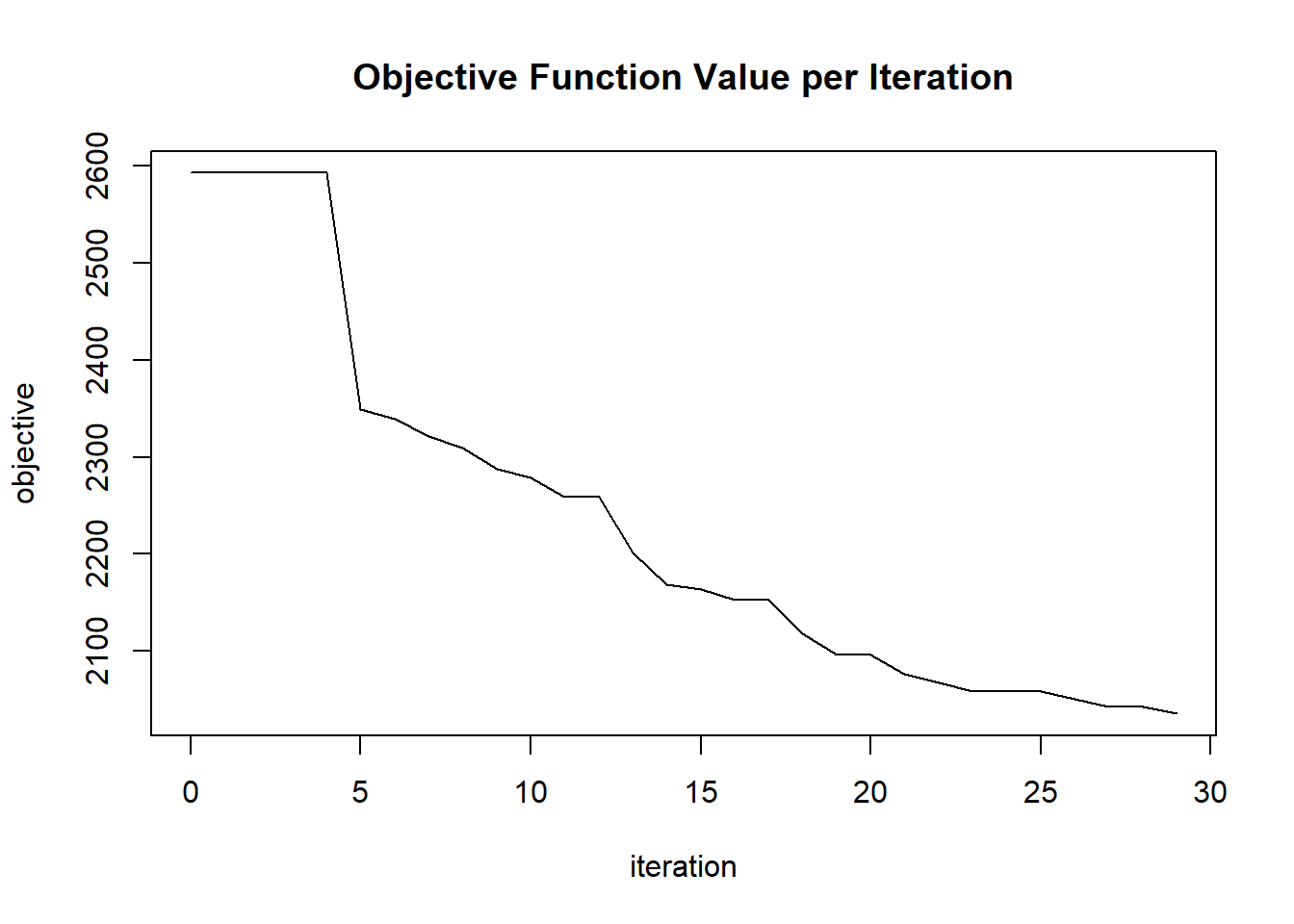
## Iteration 52 of 75 69.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 202 3 Quadratic Quadratic 1 4 NA NA
## objective
## 202 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_103
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 2382.41311
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1385.181
## Misclassification Error (Categorical): 347
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:29 0.007 sec 0 1.05000 3087.78622
## 2 2020-06-20 06:43:29 0.008 sec 1 0.70000 3087.78622
## 3 2020-06-20 06:43:29 0.010 sec 2 0.46667 3087.78622
## 4 2020-06-20 06:43:29 0.011 sec 3 0.49000 2925.93923
## 5 2020-06-20 06:43:29 0.012 sec 4 0.51450 2709.54424
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:29 0.035 sec 24 0.08943 2395.52895
## 26 2020-06-20 06:43:29 0.036 sec 25 0.05962 2395.52895
## 27 2020-06-20 06:43:29 0.037 sec 26 0.06260 2388.10168
## 28 2020-06-20 06:43:29 0.038 sec 27 0.06573 2386.68914
## 29 2020-06-20 06:43:29 0.040 sec 28 0.04382 2386.68914
## 30 2020-06-20 06:43:29 0.041 sec 29 0.04601 2382.41311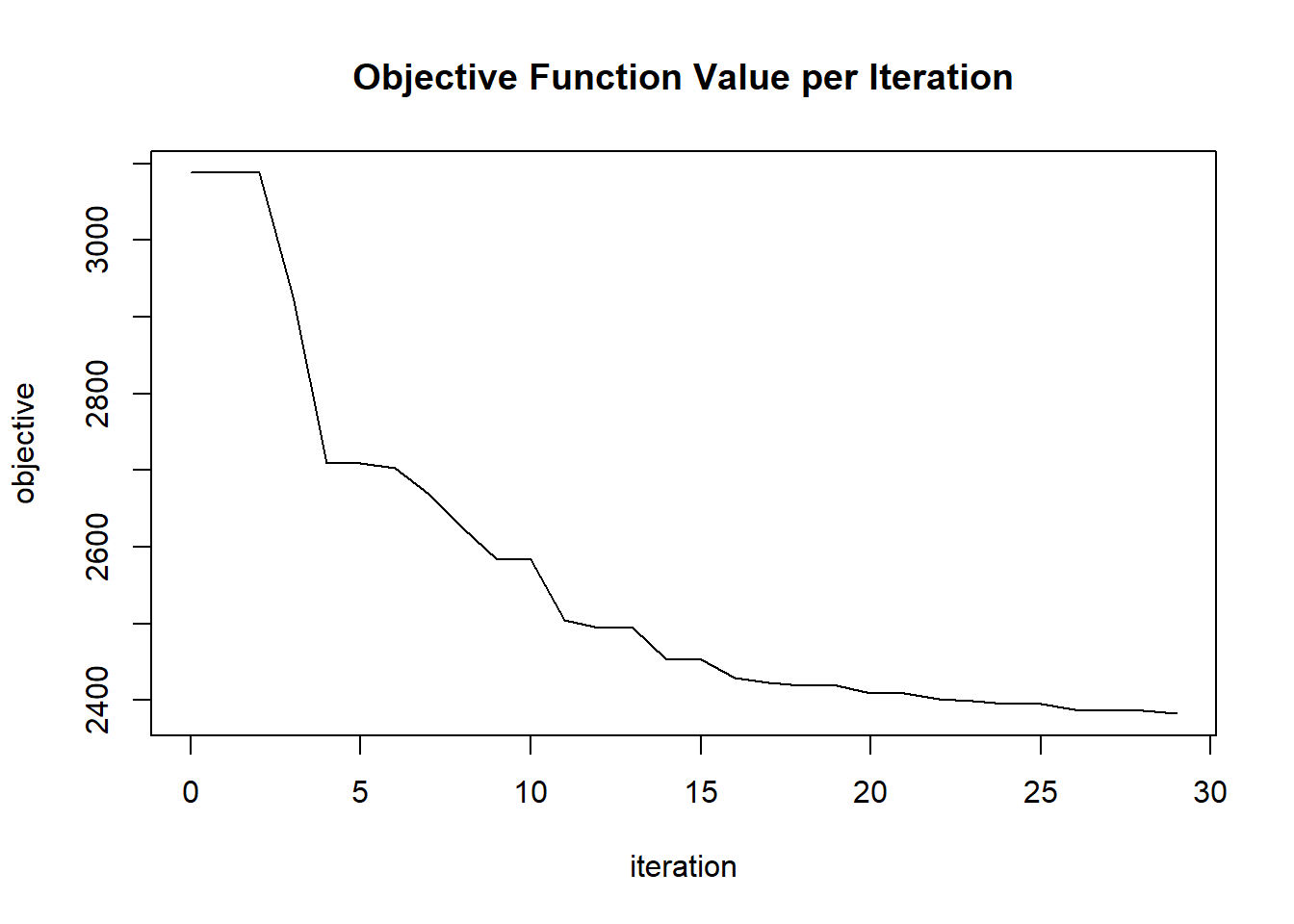
## Iteration 53 of 75 70.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 35 5 L1 None 1 0 NA NA
## objective
## 35 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_105
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.13483 1469.24301
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1253.524
## Misclassification Error (Categorical): 161
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:31 0.016 sec 0 1.05000 2379.20645
## 2 2020-06-20 06:43:31 0.019 sec 1 0.70000 2379.20645
## 3 2020-06-20 06:43:31 0.022 sec 2 0.46667 2379.20645
## 4 2020-06-20 06:43:31 0.025 sec 3 0.31111 2379.20645
## 5 2020-06-20 06:43:31 0.027 sec 4 0.15556 2379.20645
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:31 0.082 sec 24 0.16638 1509.91582
## 26 2020-06-20 06:43:31 0.085 sec 25 0.17470 1508.94434
## 27 2020-06-20 06:43:31 0.087 sec 26 0.11647 1508.94434
## 28 2020-06-20 06:43:31 0.090 sec 27 0.12229 1481.22579
## 29 2020-06-20 06:43:31 0.092 sec 28 0.12841 1471.57184
## 30 2020-06-20 06:43:31 0.094 sec 29 0.13483 1469.24301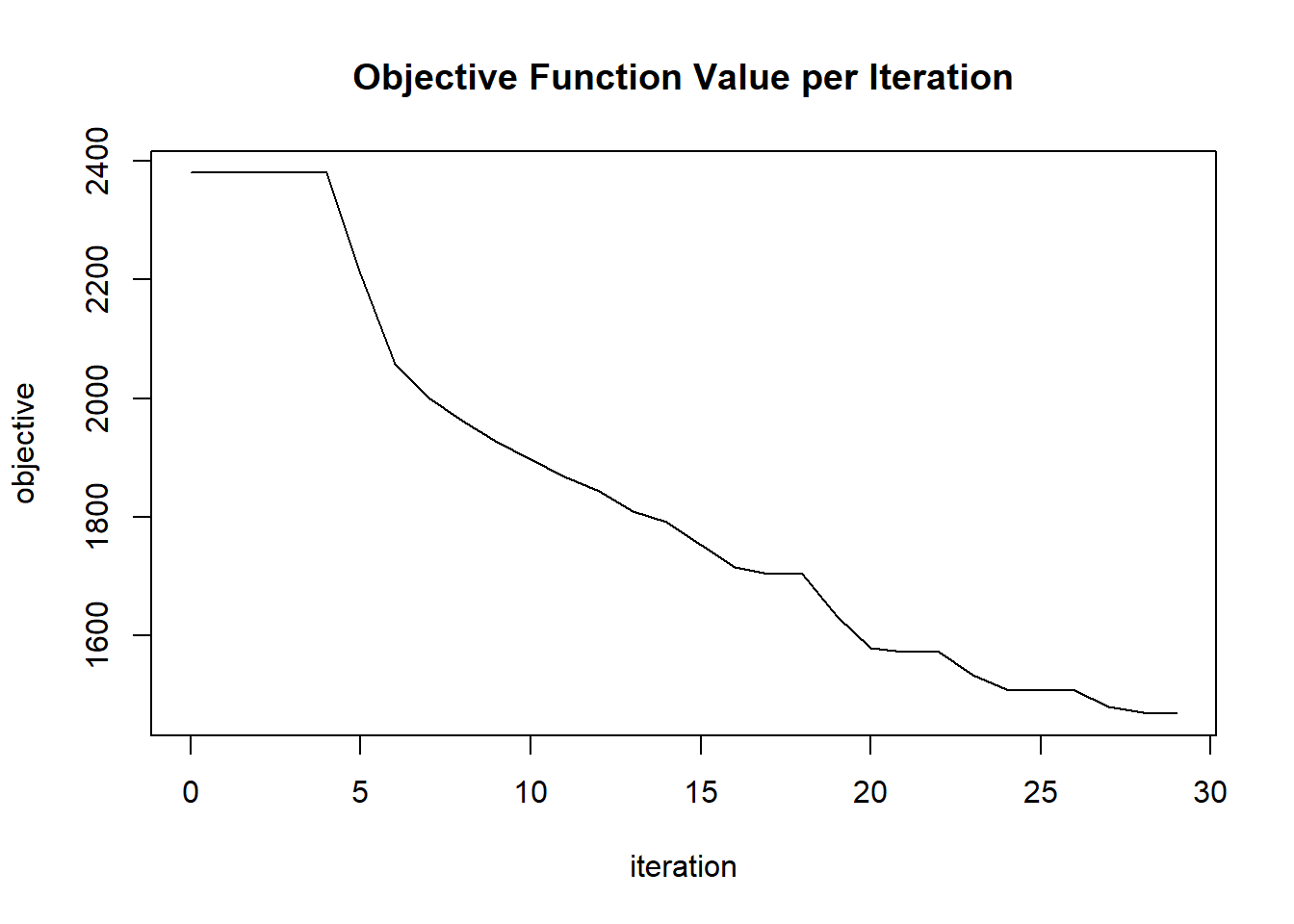
## Iteration 54 of 75 72%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 126 10 L1 Quadratic 1 1 NA NA
## objective
## 126 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_107
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 1439.28043
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 661.9937
## Misclassification Error (Categorical): 64
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:32 0.014 sec 0 1.05000 3176.64990
## 2 2020-06-20 06:43:32 0.017 sec 1 0.70000 3176.64990
## 3 2020-06-20 06:43:32 0.020 sec 2 0.46667 3176.64990
## 4 2020-06-20 06:43:32 0.022 sec 3 0.49000 2912.91125
## 5 2020-06-20 06:43:32 0.025 sec 4 0.51450 2534.38843
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:33 0.085 sec 24 0.22184 1458.24414
## 26 2020-06-20 06:43:33 0.087 sec 25 0.23294 1457.86256
## 27 2020-06-20 06:43:33 0.090 sec 26 0.15529 1457.86256
## 28 2020-06-20 06:43:33 0.093 sec 27 0.16306 1442.23305
## 29 2020-06-20 06:43:33 0.097 sec 28 0.17121 1439.95281
## 30 2020-06-20 06:43:33 0.100 sec 29 0.17977 1439.28043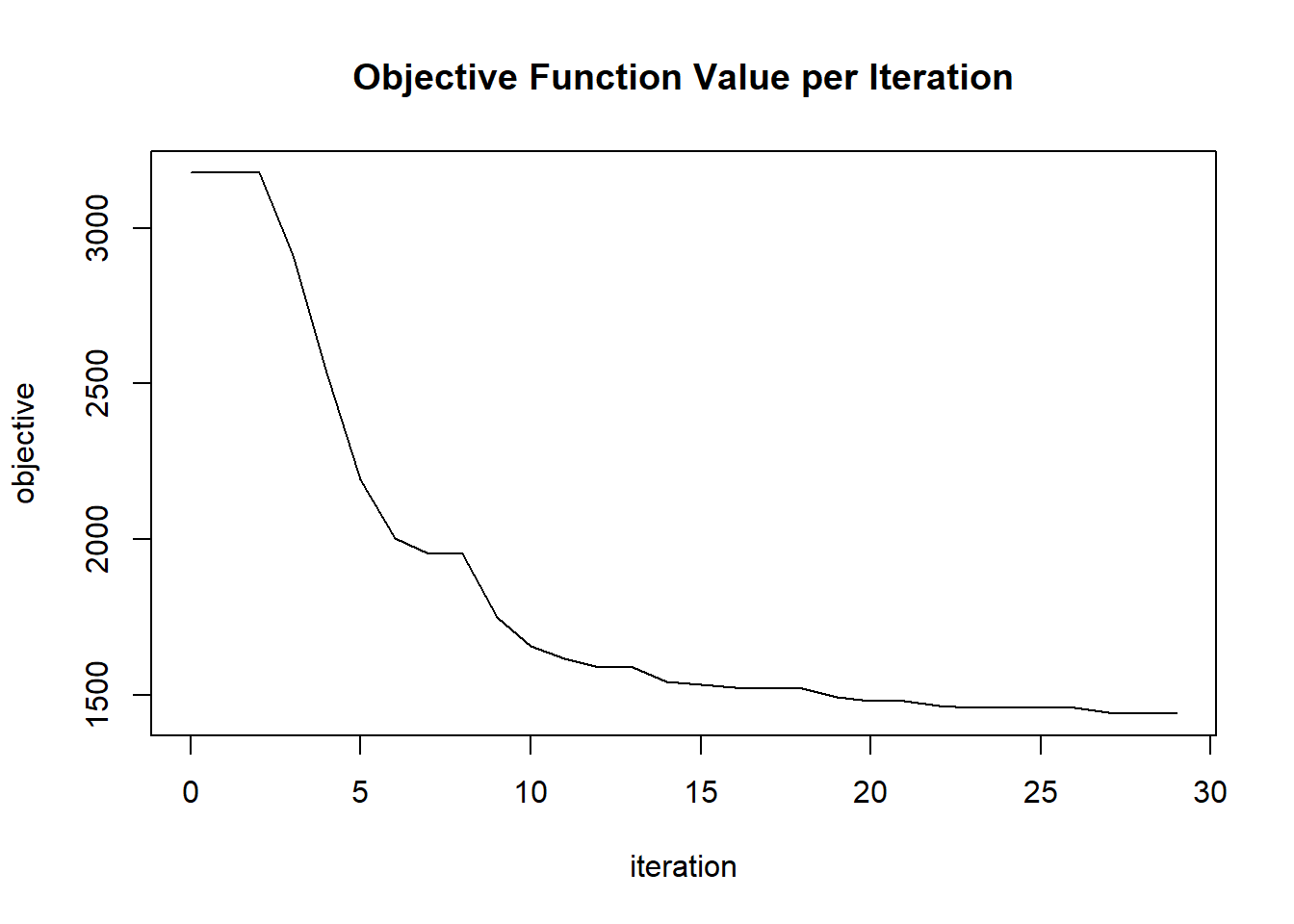
## Iteration 55 of 75 73.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 60 10 Quadratic None 4 0 NA NA
## objective
## 60 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_109
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 981.66125
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 647.399
## Misclassification Error (Categorical): 80
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:34 0.022 sec 0 1.05000 2722.88594
## 2 2020-06-20 06:43:34 0.027 sec 1 0.70000 2722.88594
## 3 2020-06-20 06:43:34 0.031 sec 2 0.46667 2722.88594
## 4 2020-06-20 06:43:34 0.034 sec 3 0.49000 2518.01305
## 5 2020-06-20 06:43:34 0.037 sec 4 0.51450 2155.04395
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:34 0.108 sec 24 0.08943 1039.03511
## 26 2020-06-20 06:43:34 0.112 sec 25 0.09390 1017.93264
## 27 2020-06-20 06:43:34 0.116 sec 26 0.09860 1007.03567
## 28 2020-06-20 06:43:34 0.120 sec 27 0.06573 1007.03567
## 29 2020-06-20 06:43:34 0.125 sec 28 0.06902 991.62423
## 30 2020-06-20 06:43:34 0.128 sec 29 0.07247 981.66125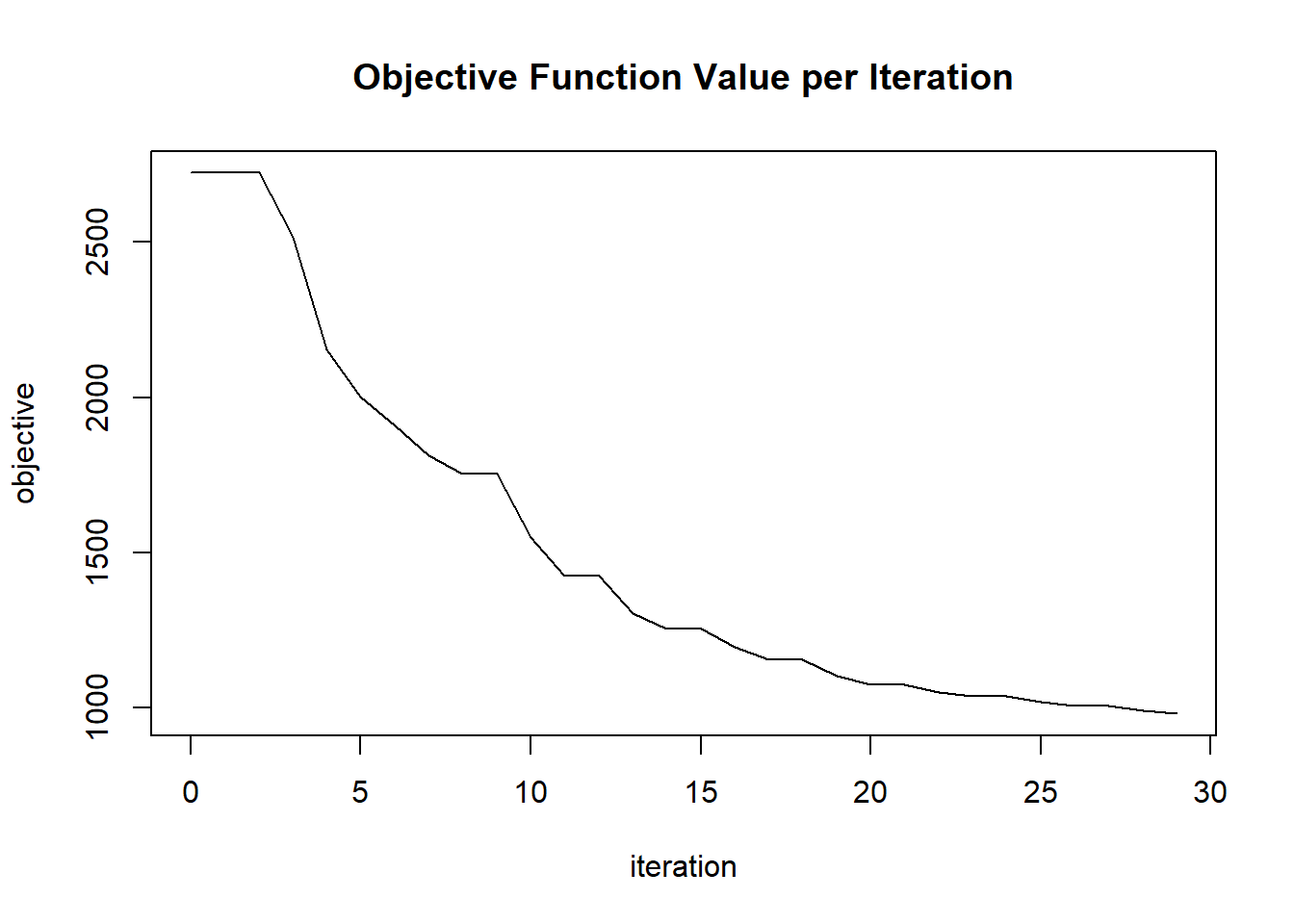
## Iteration 56 of 75 74.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 131 5 Quadratic L1 1 1 NA NA
## objective
## 131 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_111
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.21235 1465.78112
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1342.971
## Misclassification Error (Categorical): 128
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:36 0.010 sec 0 1.05000 2423.22412
## 2 2020-06-20 06:43:36 0.013 sec 1 0.70000 2423.22412
## 3 2020-06-20 06:43:36 0.015 sec 2 0.46667 2423.22412
## 4 2020-06-20 06:43:36 0.017 sec 3 0.31111 2423.22412
## 5 2020-06-20 06:43:36 0.019 sec 4 0.15556 2423.22412
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:36 0.054 sec 24 0.16638 1515.27594
## 26 2020-06-20 06:43:36 0.056 sec 25 0.17470 1487.51515
## 27 2020-06-20 06:43:36 0.057 sec 26 0.18344 1474.09548
## 28 2020-06-20 06:43:36 0.059 sec 27 0.19261 1469.96701
## 29 2020-06-20 06:43:36 0.061 sec 28 0.20224 1468.08569
## 30 2020-06-20 06:43:36 0.063 sec 29 0.21235 1465.78112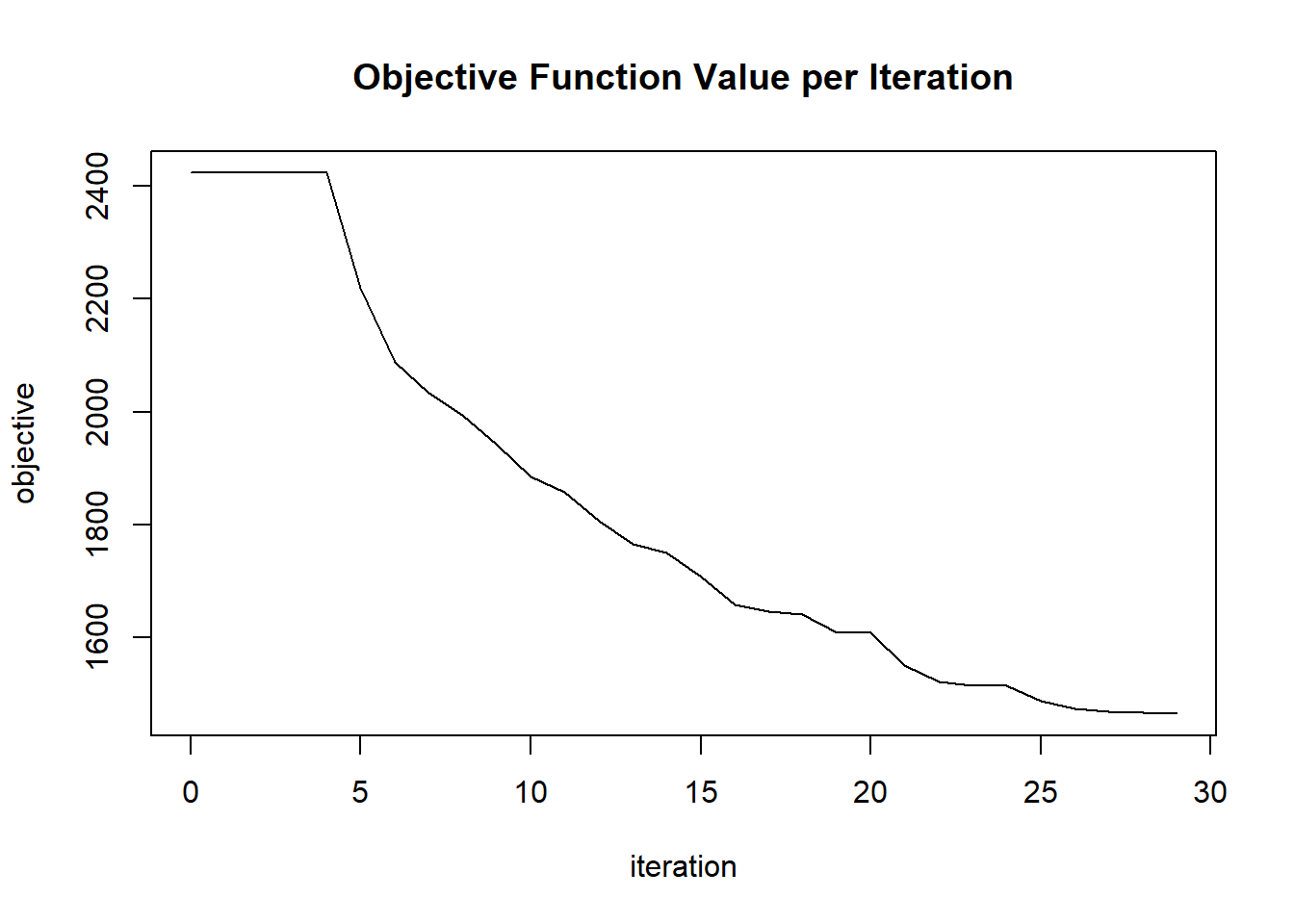
## Iteration 57 of 75 76%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 157 3 Quadratic L1 4 1 NA NA
## objective
## 157 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_113
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.03451 2295.96917
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1366.168
## Misclassification Error (Categorical): 355
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:37 0.009 sec 0 1.05000 2680.74596
## 2 2020-06-20 06:43:37 0.010 sec 1 0.70000 2680.74596
## 3 2020-06-20 06:43:37 0.011 sec 2 0.46667 2680.74596
## 4 2020-06-20 06:43:37 0.012 sec 3 0.31111 2680.74596
## 5 2020-06-20 06:43:37 0.014 sec 4 0.15556 2680.74596
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:37 0.038 sec 24 0.04259 2303.99383
## 26 2020-06-20 06:43:37 0.040 sec 25 0.02839 2303.99383
## 27 2020-06-20 06:43:37 0.041 sec 26 0.02981 2299.48278
## 28 2020-06-20 06:43:37 0.042 sec 27 0.03130 2297.90230
## 29 2020-06-20 06:43:37 0.043 sec 28 0.03287 2296.99514
## 30 2020-06-20 06:43:37 0.044 sec 29 0.03451 2295.96917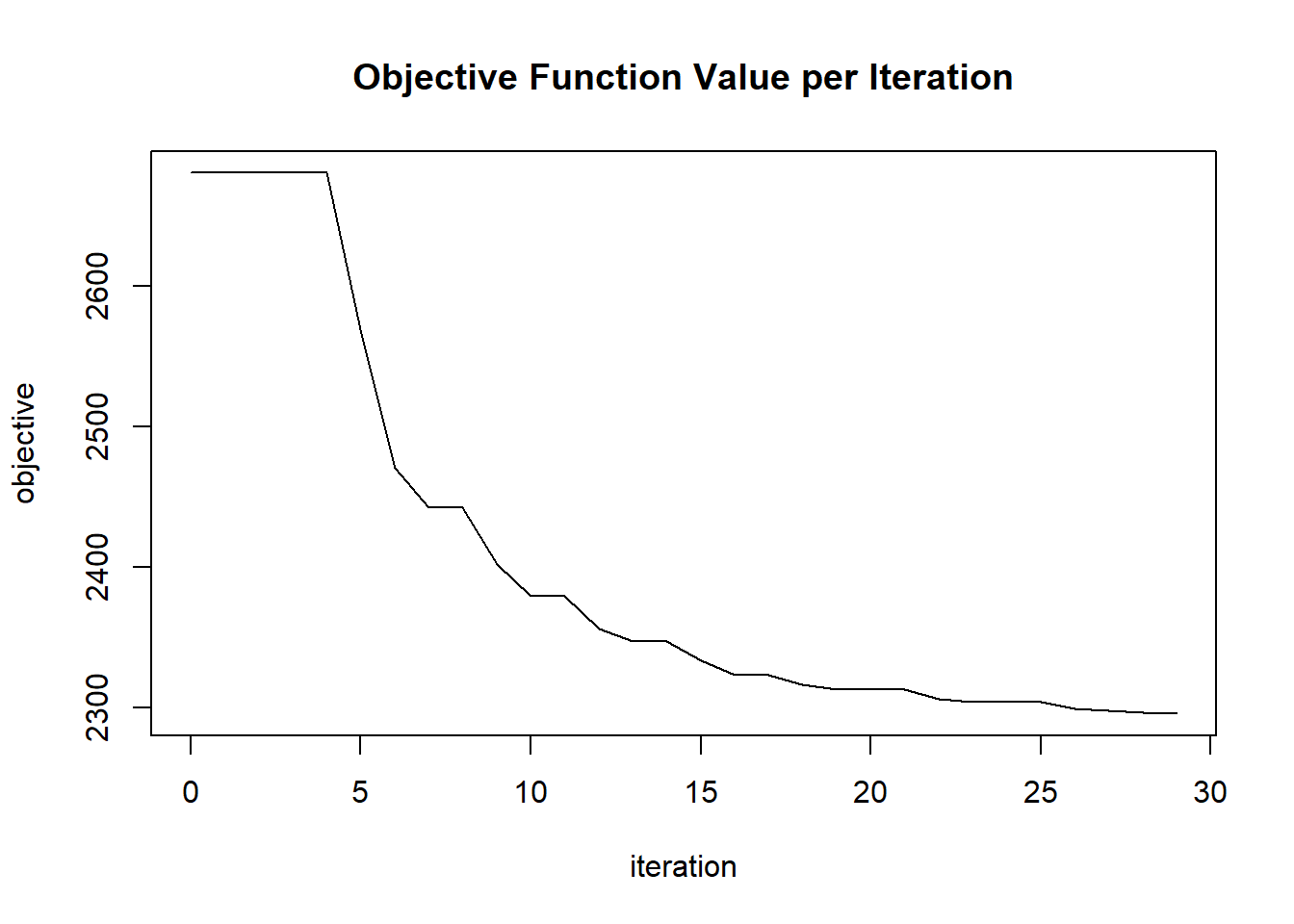
## Iteration 58 of 75 77.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 230 5 Quadratic Quadratic 4 4 NA NA
## objective
## 230 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_115
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.02921 2535.23901
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1402.348
## Misclassification Error (Categorical): 212
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:39 0.011 sec 0 1.05000 3674.26175
## 2 2020-06-20 06:43:39 0.013 sec 1 0.70000 3674.26175
## 3 2020-06-20 06:43:39 0.015 sec 2 0.46667 3674.26175
## 4 2020-06-20 06:43:39 0.017 sec 3 0.49000 3101.95275
## 5 2020-06-20 06:43:39 0.019 sec 4 0.51450 3028.27486
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:39 0.057 sec 24 0.05678 2546.78079
## 26 2020-06-20 06:43:39 0.060 sec 25 0.03785 2546.78079
## 27 2020-06-20 06:43:39 0.062 sec 26 0.03975 2540.01539
## 28 2020-06-20 06:43:39 0.064 sec 27 0.02650 2540.01539
## 29 2020-06-20 06:43:39 0.067 sec 28 0.02782 2536.02364
## 30 2020-06-20 06:43:39 0.069 sec 29 0.02921 2535.23901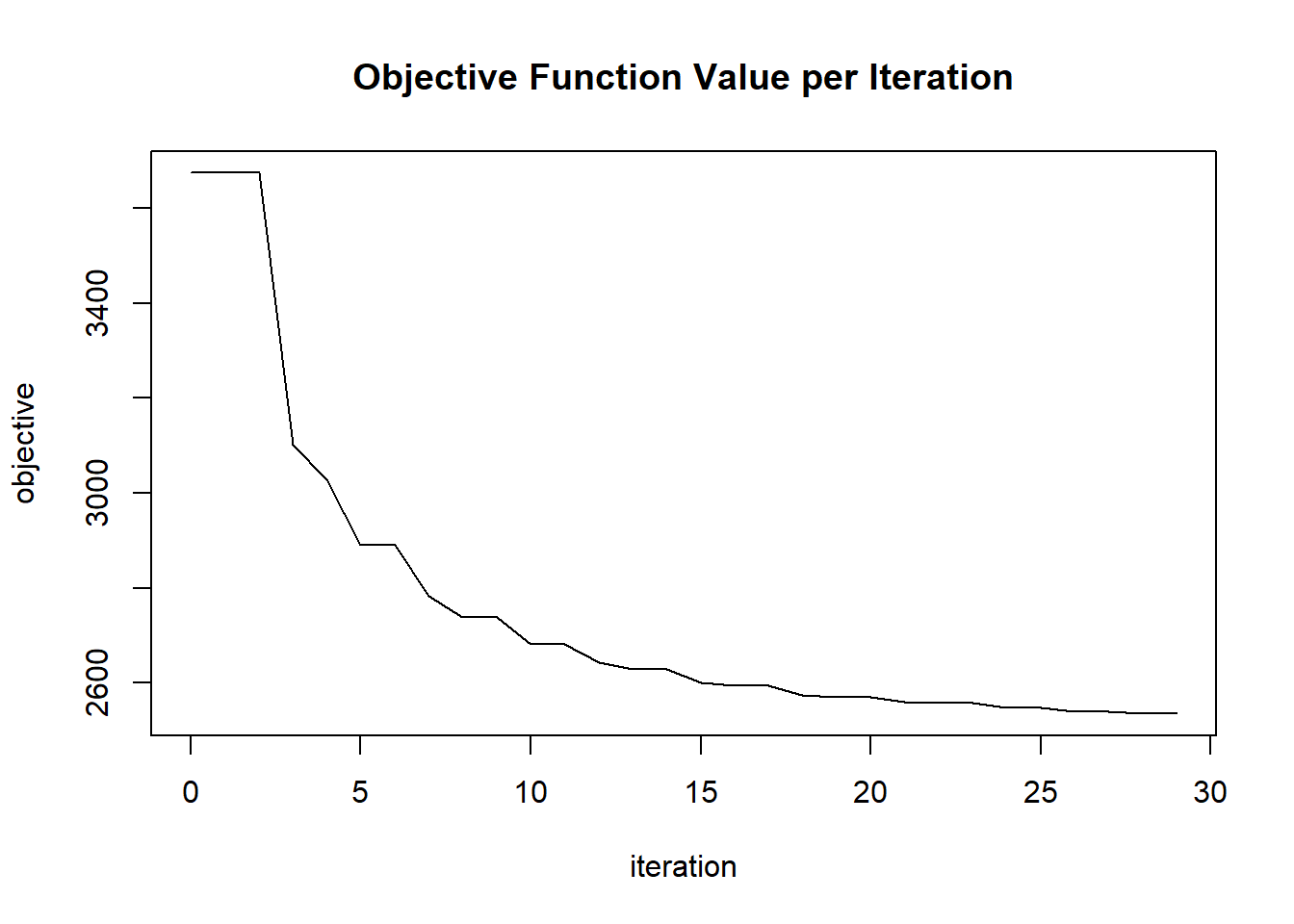
## Iteration 59 of 75 78.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 59 5 Quadratic None 4 0 NA NA
## objective
## 59 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_117
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 1479.64579
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1320.759
## Misclassification Error (Categorical): 163
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:40 0.015 sec 0 1.05000 2645.00054
## 2 2020-06-20 06:43:40 0.017 sec 1 0.70000 2645.00054
## 3 2020-06-20 06:43:40 0.019 sec 2 0.46667 2645.00054
## 4 2020-06-20 06:43:40 0.021 sec 3 0.31111 2645.00054
## 5 2020-06-20 06:43:40 0.024 sec 4 0.32667 2512.70148
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:41 0.071 sec 24 0.08943 1540.83775
## 26 2020-06-20 06:43:41 0.073 sec 25 0.09390 1512.42096
## 27 2020-06-20 06:43:41 0.075 sec 26 0.09860 1504.16126
## 28 2020-06-20 06:43:41 0.077 sec 27 0.06573 1504.16126
## 29 2020-06-20 06:43:41 0.079 sec 28 0.06902 1486.64945
## 30 2020-06-20 06:43:41 0.081 sec 29 0.07247 1479.64579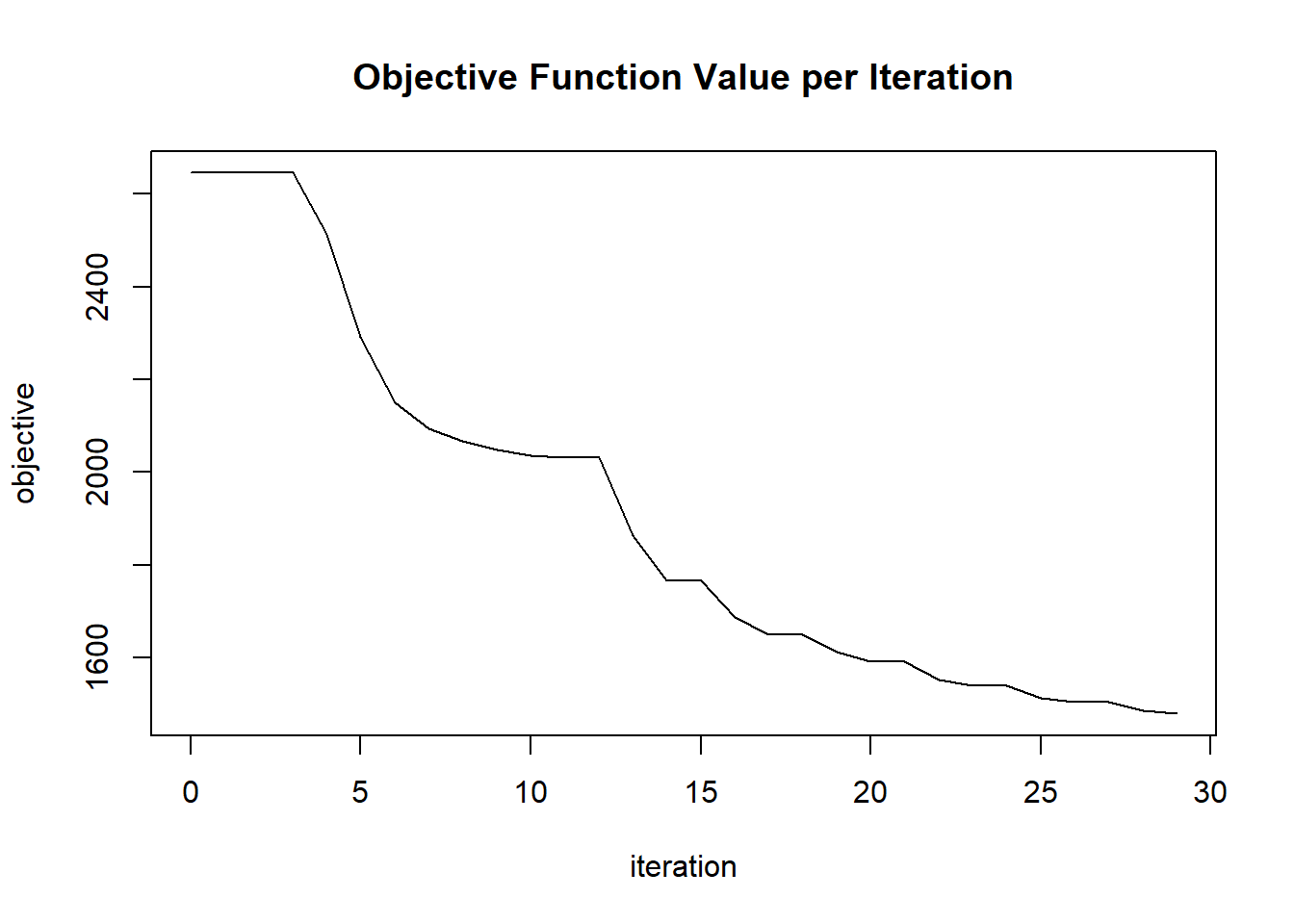
## Iteration 60 of 75 80%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 125 5 L1 Quadratic 1 1 NA NA
## objective
## 125 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_119
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 1691.11410
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1381.535
## Misclassification Error (Categorical): 119
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:42 0.014 sec 0 1.05000 2737.51174
## 2 2020-06-20 06:43:42 0.016 sec 1 0.70000 2737.51174
## 3 2020-06-20 06:43:42 0.018 sec 2 0.46667 2737.51174
## 4 2020-06-20 06:43:42 0.020 sec 3 0.31111 2737.51174
## 5 2020-06-20 06:43:42 0.022 sec 4 0.32667 2620.55106
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:42 0.058 sec 24 0.22184 1710.78109
## 26 2020-06-20 06:43:42 0.060 sec 25 0.14790 1710.78109
## 27 2020-06-20 06:43:42 0.062 sec 26 0.15529 1696.06760
## 28 2020-06-20 06:43:42 0.064 sec 27 0.16306 1695.02818
## 29 2020-06-20 06:43:42 0.065 sec 28 0.17121 1693.57804
## 30 2020-06-20 06:43:42 0.067 sec 29 0.17977 1691.11410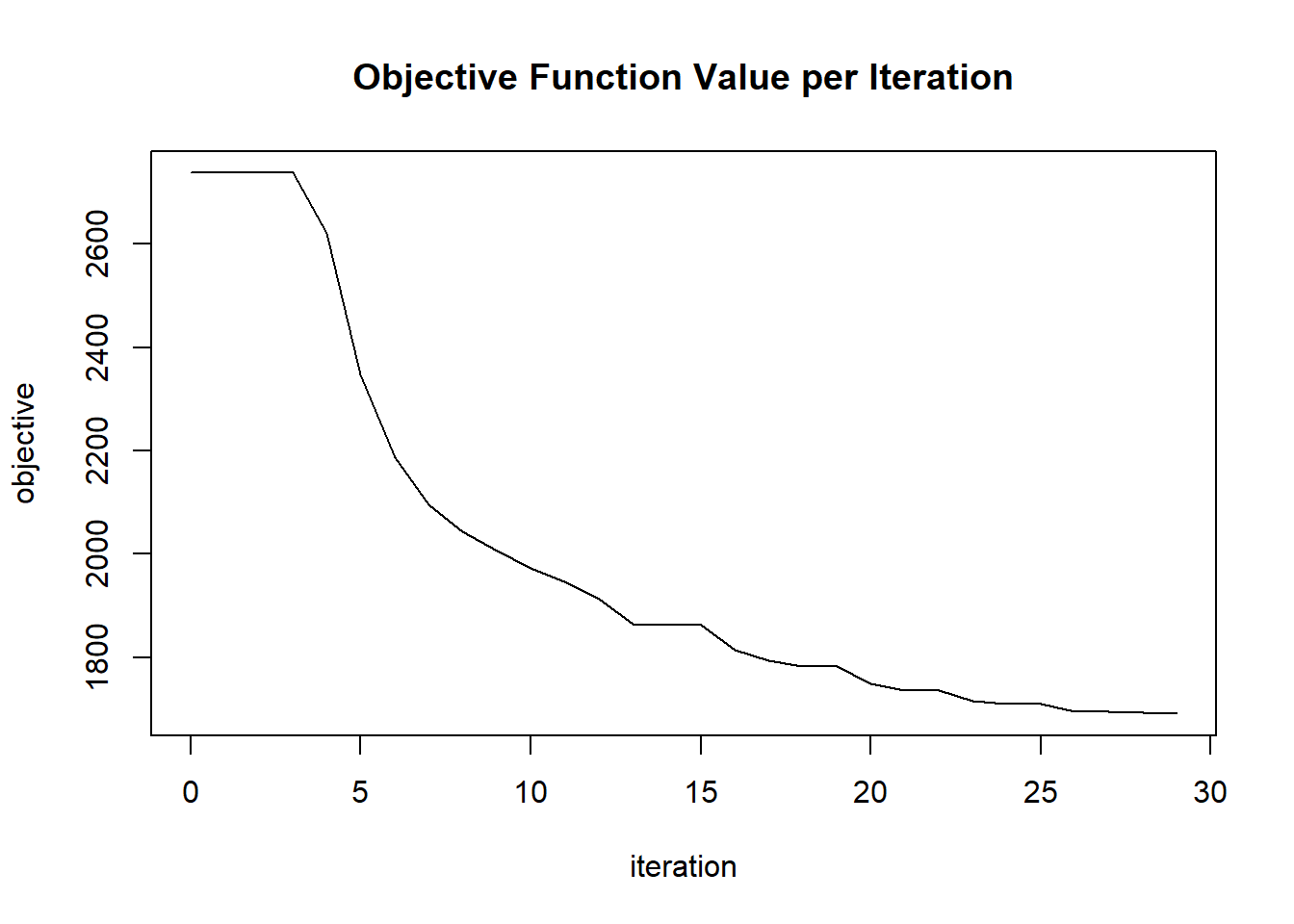
## Iteration 61 of 75 81.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 31 3 Quadratic None 1 0 NA NA
## objective
## 31 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_121
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.02191 1980.70675
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1303.308
## Misclassification Error (Categorical): 354
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:44 0.014 sec 0 1.05000 2361.95790
## 2 2020-06-20 06:43:44 0.016 sec 1 0.70000 2361.95790
## 3 2020-06-20 06:43:44 0.018 sec 2 0.46667 2361.95790
## 4 2020-06-20 06:43:44 0.020 sec 3 0.31111 2361.95790
## 5 2020-06-20 06:43:44 0.021 sec 4 0.15556 2361.95790
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:44 0.059 sec 24 0.02704 1989.44120
## 26 2020-06-20 06:43:44 0.060 sec 25 0.02839 1985.78826
## 27 2020-06-20 06:43:44 0.062 sec 26 0.02981 1983.67927
## 28 2020-06-20 06:43:44 0.064 sec 27 0.01987 1983.67927
## 29 2020-06-20 06:43:44 0.066 sec 28 0.02087 1981.74356
## 30 2020-06-20 06:43:44 0.067 sec 29 0.02191 1980.70675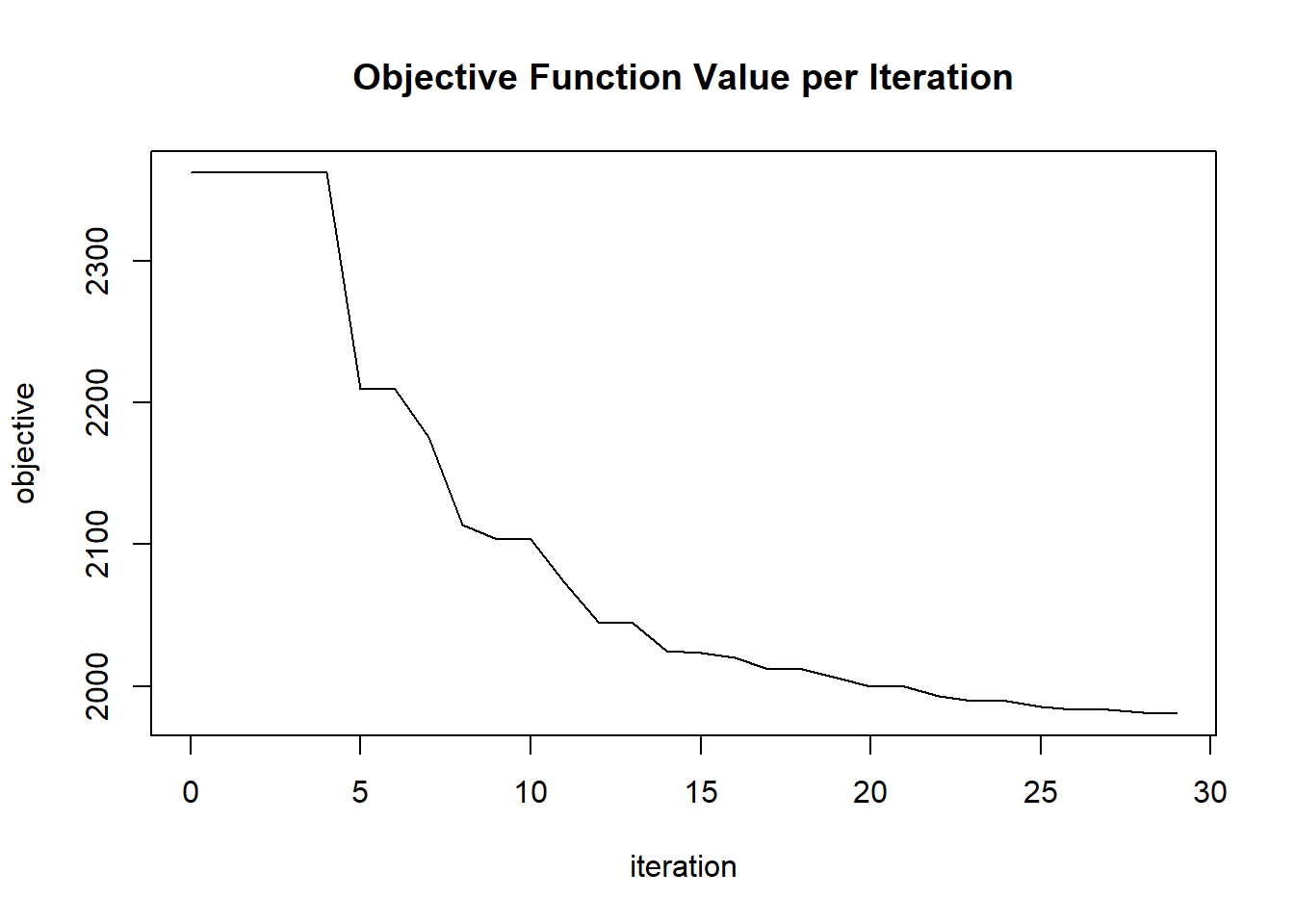
## Iteration 62 of 75 82.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 133 3 L1 L1 1 1 NA NA
## objective
## 133 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_123
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.03451 2240.16322
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1335.423
## Misclassification Error (Categorical): 355
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:45 0.007 sec 0 1.05000 2538.85947
## 2 2020-06-20 06:43:45 0.008 sec 1 0.70000 2538.85947
## 3 2020-06-20 06:43:45 0.009 sec 2 0.46667 2538.85947
## 4 2020-06-20 06:43:45 0.011 sec 3 0.31111 2538.85947
## 5 2020-06-20 06:43:45 0.012 sec 4 0.15556 2538.85947
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:45 0.034 sec 24 0.04259 2246.02788
## 26 2020-06-20 06:43:45 0.036 sec 25 0.02839 2246.02788
## 27 2020-06-20 06:43:45 0.037 sec 26 0.02981 2242.97007
## 28 2020-06-20 06:43:45 0.038 sec 27 0.03130 2241.27268
## 29 2020-06-20 06:43:45 0.039 sec 28 0.03287 2240.67605
## 30 2020-06-20 06:43:45 0.040 sec 29 0.03451 2240.16322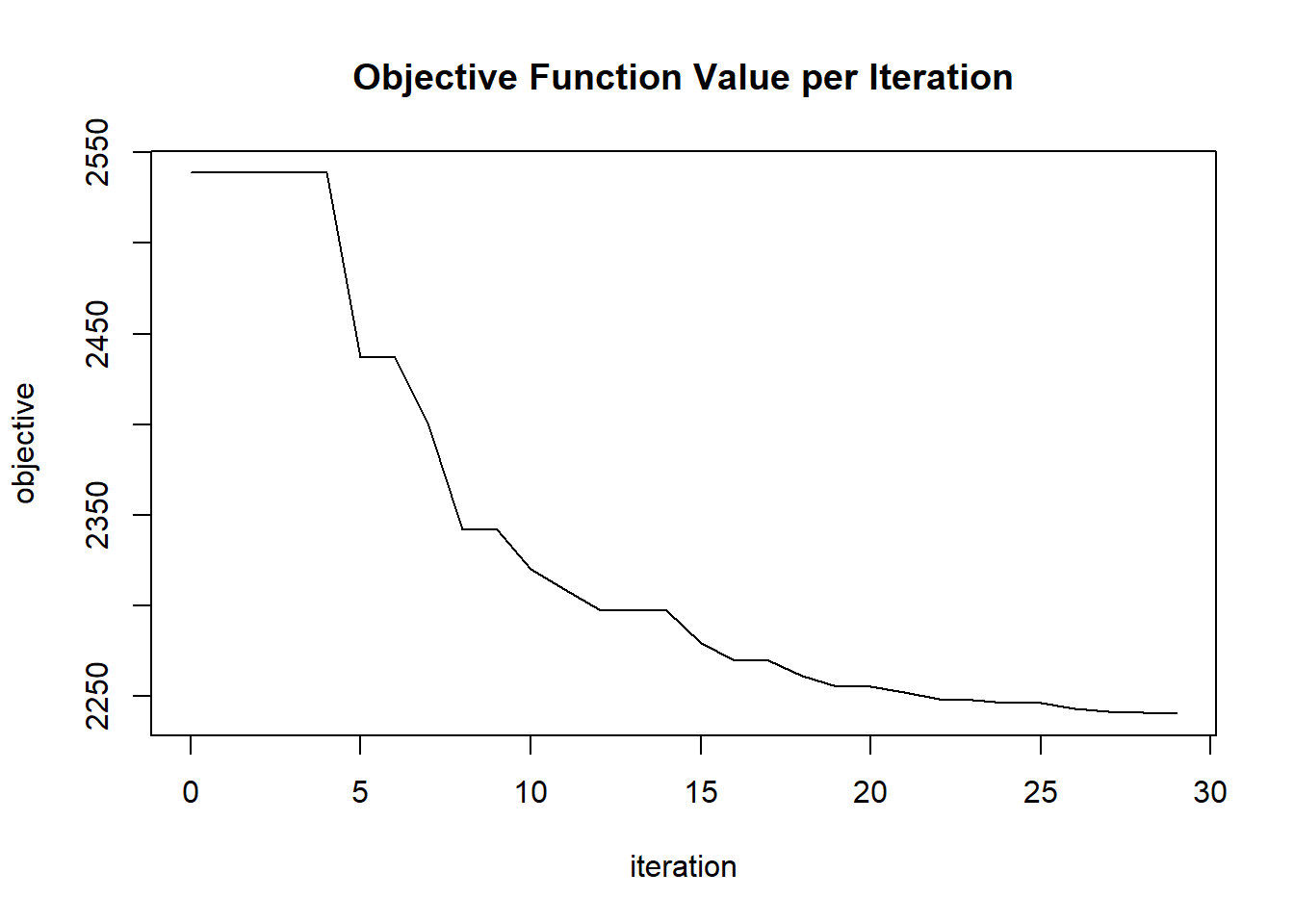
## Iteration 63 of 75 84%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 174 10 None Quadratic 0 4 NA NA
## objective
## 174 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_125
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 1030.77243
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 763.3506
## Misclassification Error (Categorical): 88
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:47 0.015 sec 0 1.05000 3764.32117
## 2 2020-06-20 06:43:47 0.018 sec 1 0.70000 3764.32117
## 3 2020-06-20 06:43:47 0.020 sec 2 0.46667 3764.32117
## 4 2020-06-20 06:43:47 0.023 sec 3 0.49000 2697.61615
## 5 2020-06-20 06:43:47 0.026 sec 4 0.51450 2532.64445
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:47 0.084 sec 24 0.14085 1061.26164
## 26 2020-06-20 06:43:47 0.087 sec 25 0.09390 1061.26164
## 27 2020-06-20 06:43:47 0.090 sec 26 0.09860 1045.75681
## 28 2020-06-20 06:43:47 0.093 sec 27 0.10353 1035.15837
## 29 2020-06-20 06:43:47 0.096 sec 28 0.10870 1030.77243
## 30 2020-06-20 06:43:47 0.099 sec 29 0.07247 1030.77243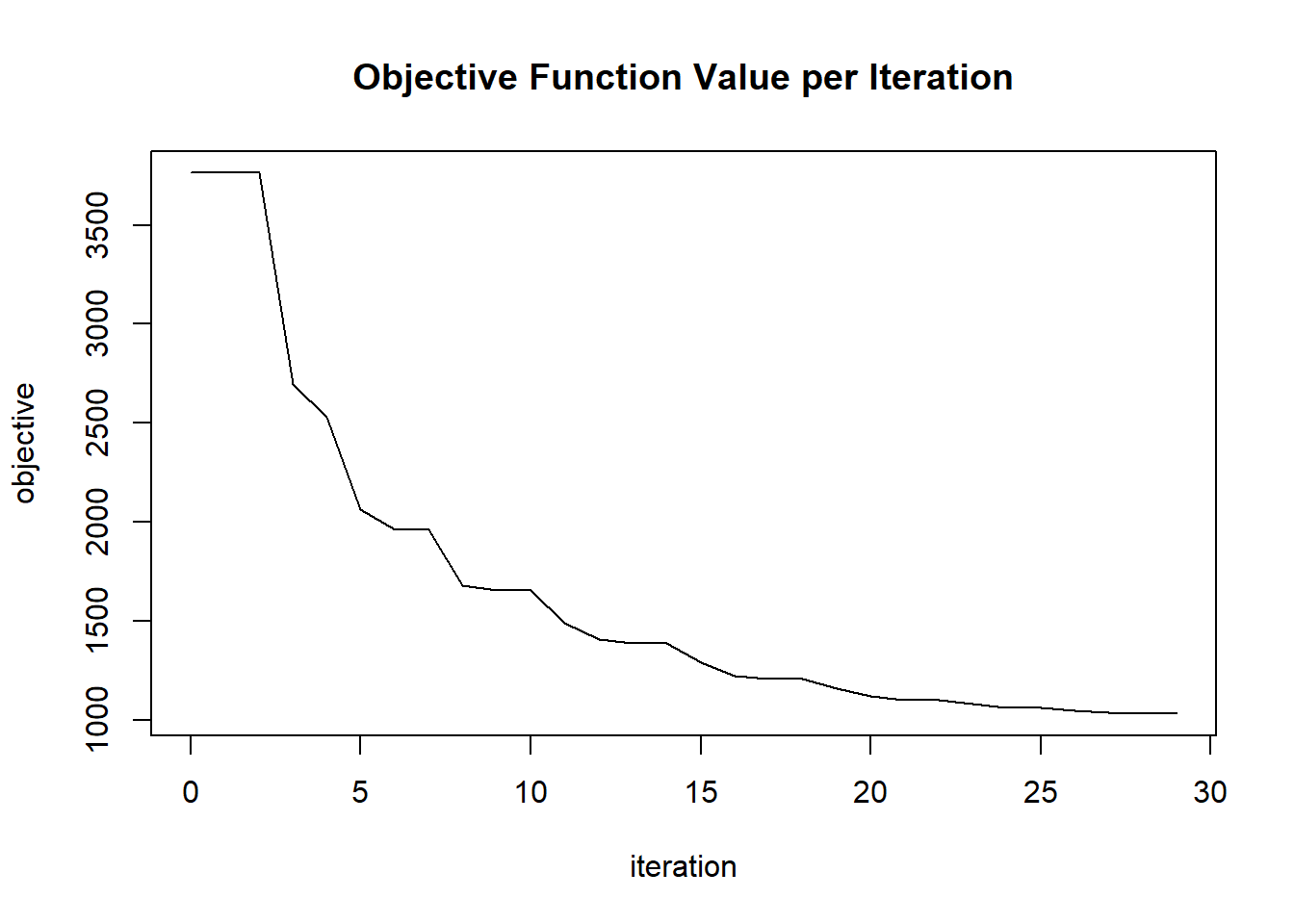
## Iteration 64 of 75 85.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 229 3 Quadratic Quadratic 4 4 NA NA
## objective
## 229 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_127
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 2792.10133
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1468.129
## Misclassification Error (Categorical): 357
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:49 0.011 sec 0 1.05000 3576.71003
## 2 2020-06-20 06:43:49 0.013 sec 1 0.70000 3576.71003
## 3 2020-06-20 06:43:49 0.015 sec 2 0.46667 3576.71003
## 4 2020-06-20 06:43:49 0.018 sec 3 0.49000 3390.36989
## 5 2020-06-20 06:43:49 0.019 sec 4 0.51450 3319.57170
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:49 0.056 sec 24 0.08943 2803.76222
## 26 2020-06-20 06:43:49 0.058 sec 25 0.05962 2803.76222
## 27 2020-06-20 06:43:49 0.059 sec 26 0.06260 2797.03216
## 28 2020-06-20 06:43:49 0.062 sec 27 0.06573 2793.97543
## 29 2020-06-20 06:43:49 0.063 sec 28 0.04382 2793.97543
## 30 2020-06-20 06:43:49 0.065 sec 29 0.04601 2792.10133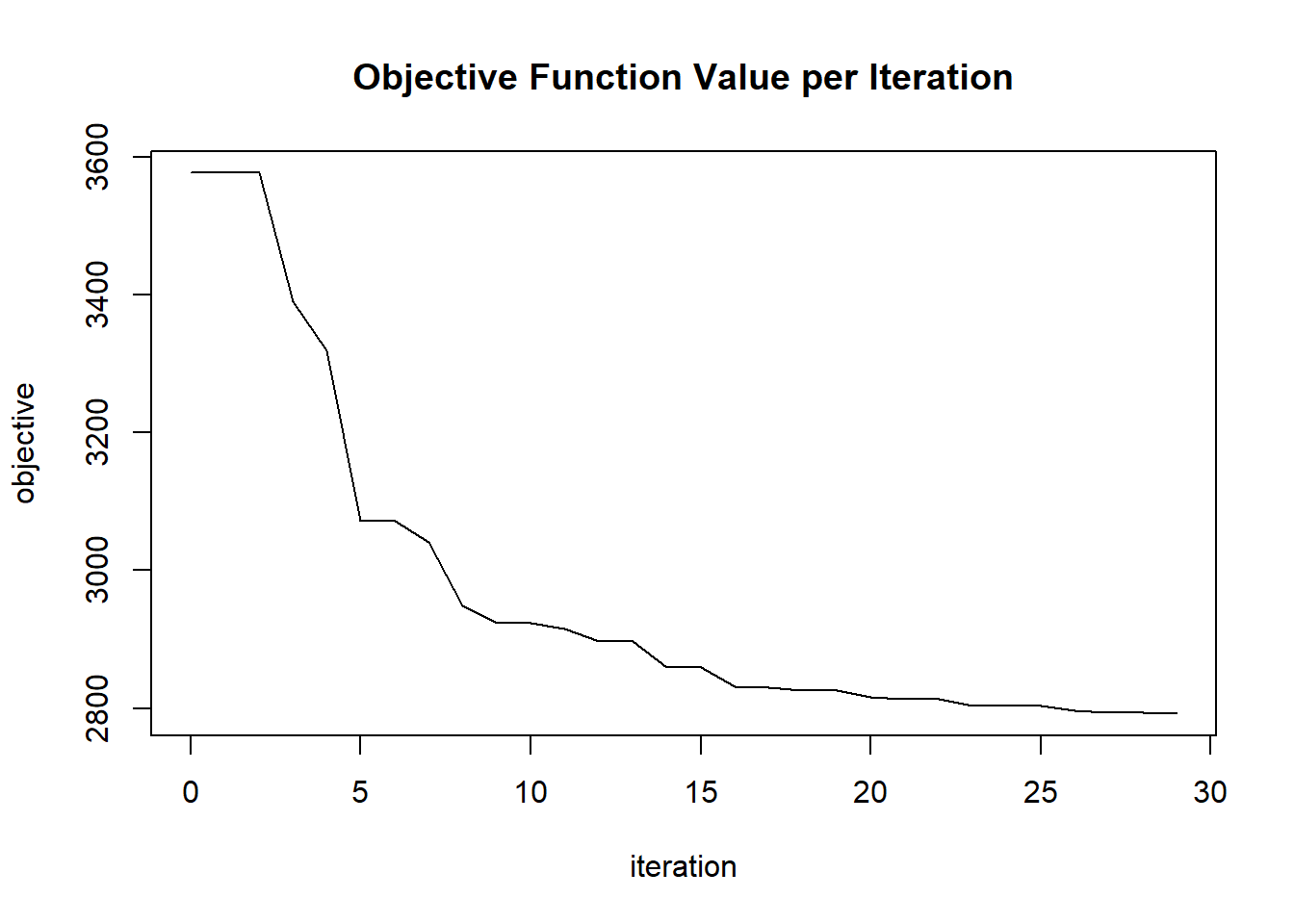
## Iteration 65 of 75 86.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 215 5 L1 L1 1 4 NA NA
## objective
## 215 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_129
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.11414 1979.80661
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1363.845
## Misclassification Error (Categorical): 155
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:50 0.012 sec 0 1.05000 3103.76931
## 2 2020-06-20 06:43:50 0.013 sec 1 0.70000 3103.76931
## 3 2020-06-20 06:43:50 0.015 sec 2 0.46667 3103.76931
## 4 2020-06-20 06:43:50 0.017 sec 3 0.31111 3103.76931
## 5 2020-06-20 06:43:50 0.019 sec 4 0.32667 2932.29197
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:50 0.052 sec 24 0.14085 1997.76617
## 26 2020-06-20 06:43:50 0.054 sec 25 0.14790 1991.32144
## 27 2020-06-20 06:43:50 0.055 sec 26 0.09860 1991.32144
## 28 2020-06-20 06:43:50 0.057 sec 27 0.10353 1983.69656
## 29 2020-06-20 06:43:50 0.059 sec 28 0.10870 1981.69351
## 30 2020-06-20 06:43:50 0.060 sec 29 0.11414 1979.80661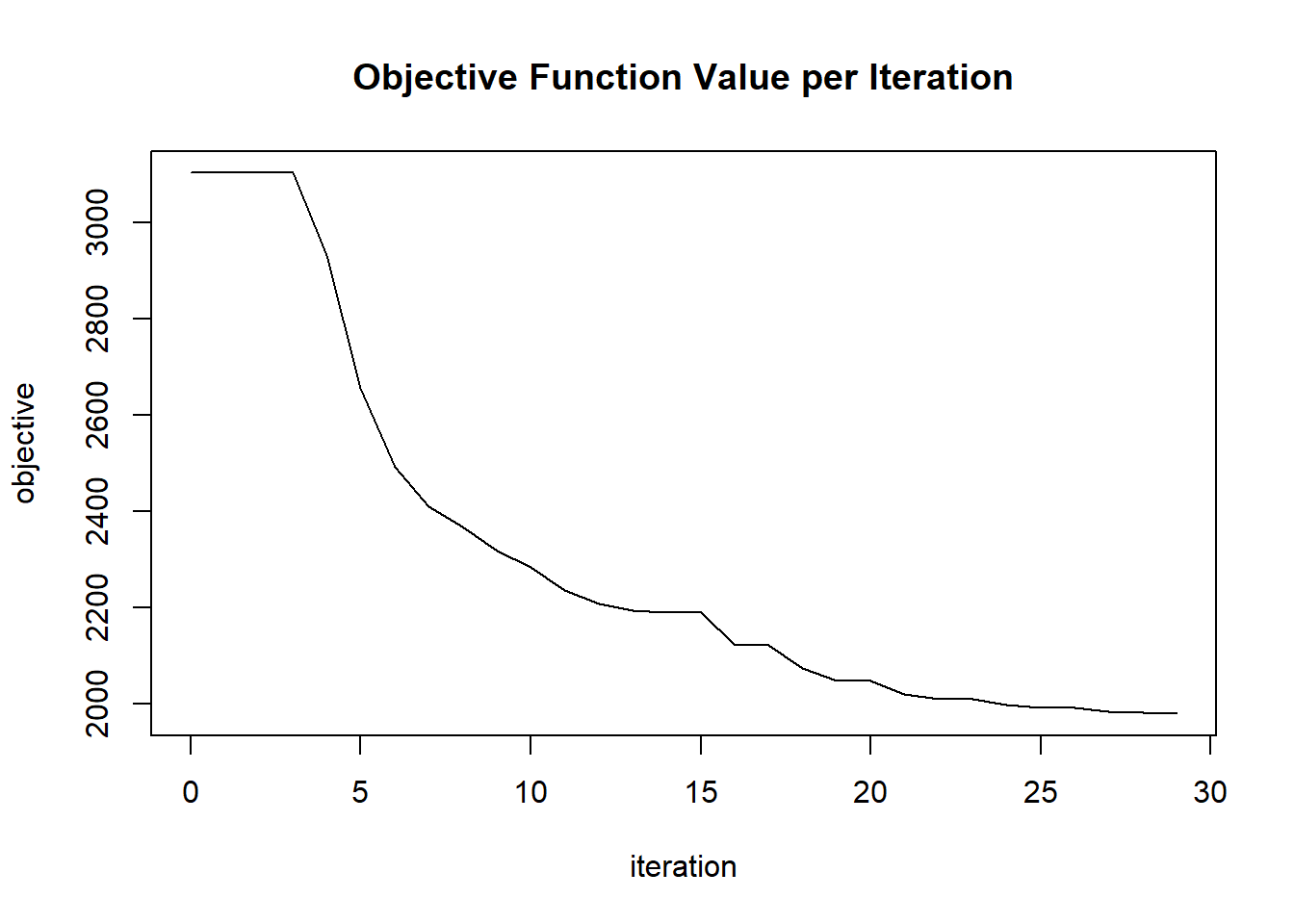
## Iteration 66 of 75 88%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 132 10 Quadratic L1 1 1 NA NA
## objective
## 132 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_131
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 952.81238
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 641.0921
## Misclassification Error (Categorical): 43
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:52 0.016 sec 0 1.05000 3035.56219
## 2 2020-06-20 06:43:52 0.019 sec 1 0.70000 3035.56219
## 3 2020-06-20 06:43:52 0.022 sec 2 0.46667 3035.56219
## 4 2020-06-20 06:43:52 0.025 sec 3 0.49000 2992.41193
## 5 2020-06-20 06:43:52 0.029 sec 4 0.51450 2622.23349
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:52 0.094 sec 24 0.22184 1003.63025
## 26 2020-06-20 06:43:52 0.099 sec 25 0.23294 978.22534
## 27 2020-06-20 06:43:52 0.102 sec 26 0.24458 971.83686
## 28 2020-06-20 06:43:52 0.107 sec 27 0.25681 968.97555
## 29 2020-06-20 06:43:52 0.111 sec 28 0.17121 968.97555
## 30 2020-06-20 06:43:52 0.115 sec 29 0.17977 952.81238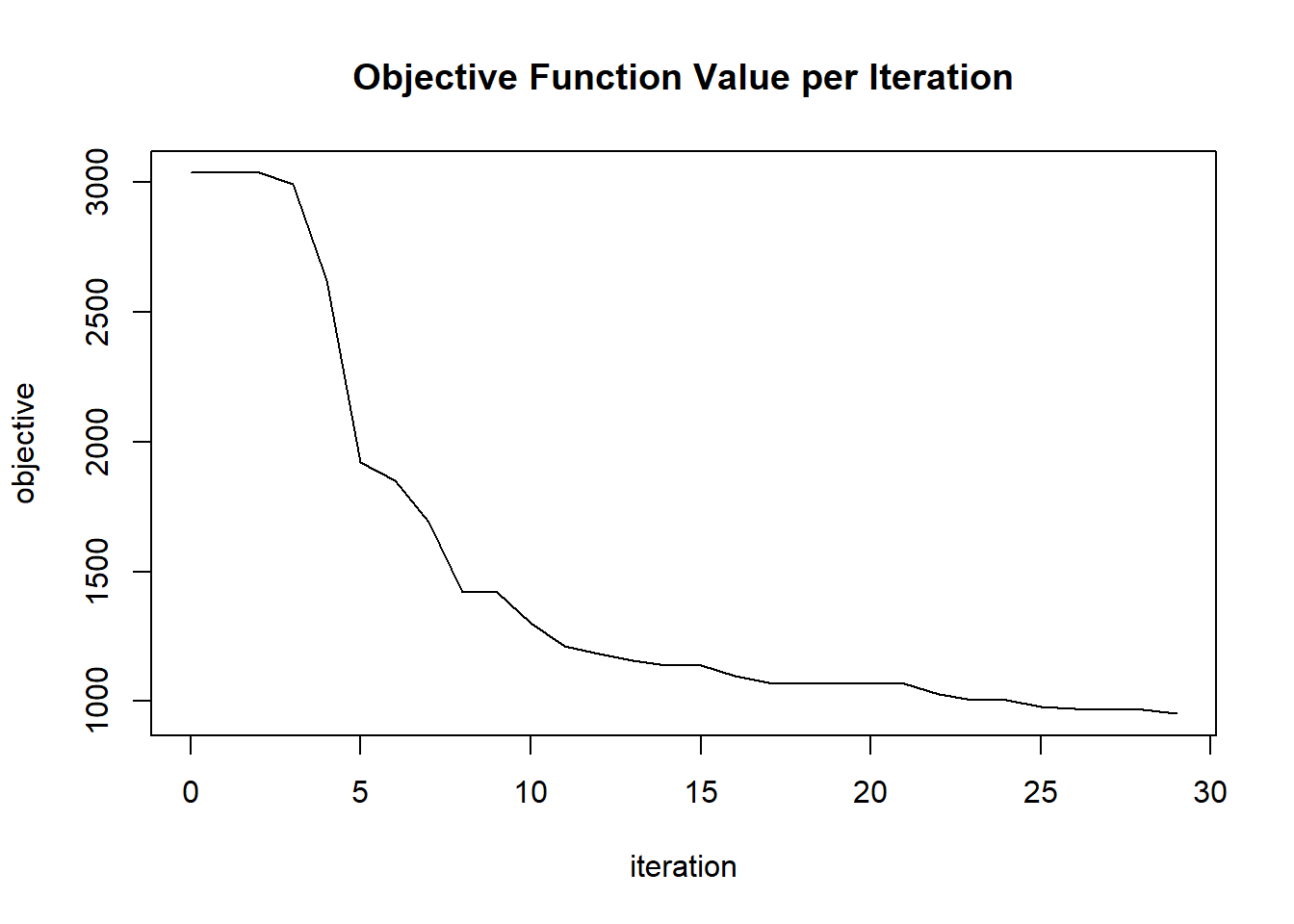
## Iteration 67 of 75 89.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 243 10 L1 L1 4 4 NA NA
## objective
## 243 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_133
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 2863.37569
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1546.808
## Misclassification Error (Categorical): 200
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:54 0.019 sec 0 1.05000 4951.02309
## 2 2020-06-20 06:43:54 0.024 sec 1 1.10250 4625.24092
## 3 2020-06-20 06:43:54 0.028 sec 2 0.73500 4625.24092
## 4 2020-06-20 06:43:54 0.033 sec 3 0.49000 4625.24092
## 5 2020-06-20 06:43:54 0.038 sec 4 0.32667 4625.24092
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:54 0.105 sec 24 0.14085 2921.01133
## 26 2020-06-20 06:43:54 0.108 sec 25 0.14790 2900.58588
## 27 2020-06-20 06:43:54 0.112 sec 26 0.09860 2900.58588
## 28 2020-06-20 06:43:54 0.114 sec 27 0.10353 2876.39636
## 29 2020-06-20 06:43:54 0.117 sec 28 0.10870 2863.37569
## 30 2020-06-20 06:43:54 0.120 sec 29 0.07247 2863.37569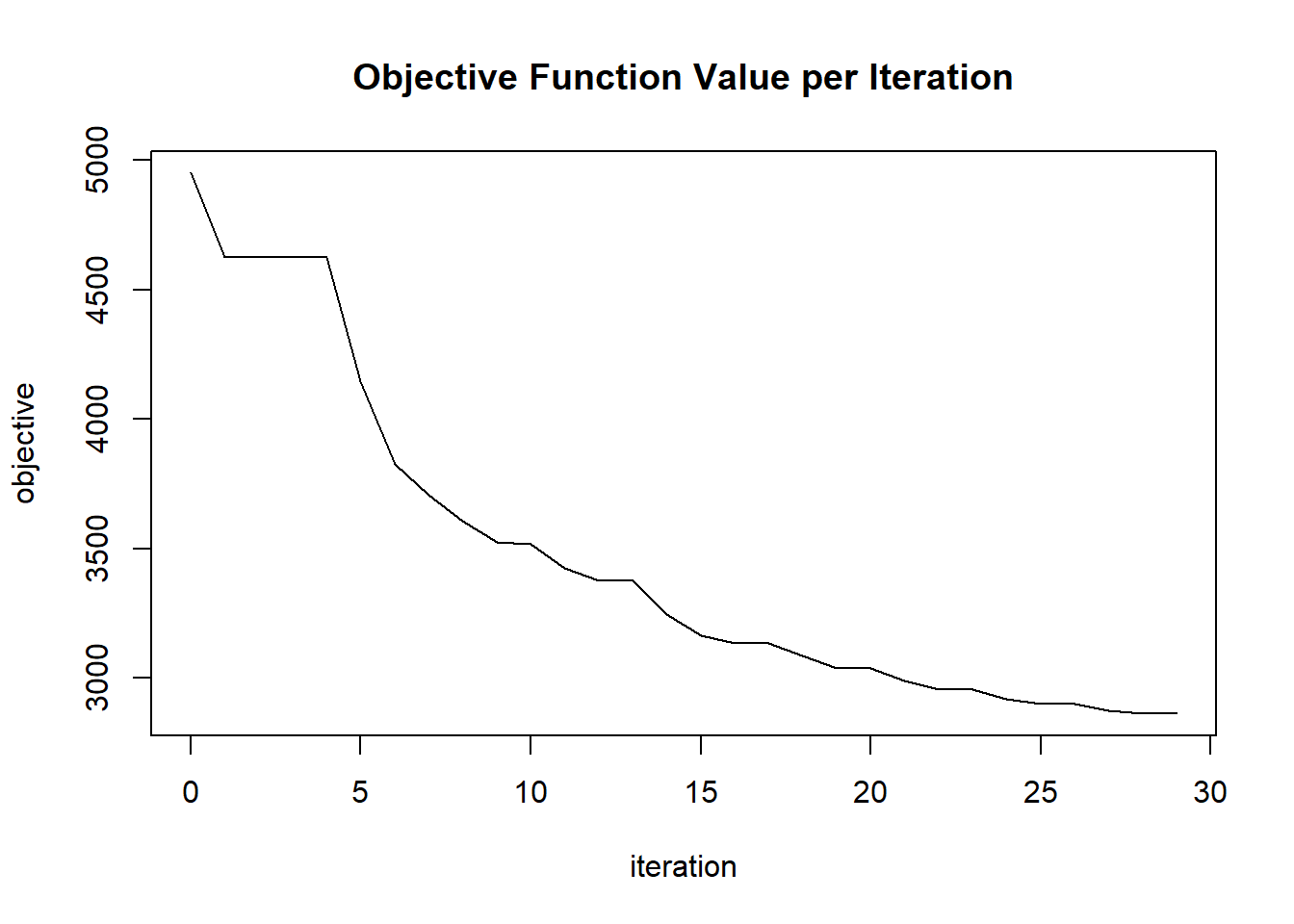
## Iteration 68 of 75 90.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 211 3 Quadratic L1 1 4 NA NA
## objective
## 211 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_135
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.21235 2429.05352
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1424.825
## Misclassification Error (Categorical): 294
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:55 0.008 sec 0 1.05000 2893.12548
## 2 2020-06-20 06:43:55 0.009 sec 1 0.70000 2893.12548
## 3 2020-06-20 06:43:55 0.010 sec 2 0.46667 2893.12548
## 4 2020-06-20 06:43:55 0.012 sec 3 0.31111 2893.12548
## 5 2020-06-20 06:43:55 0.013 sec 4 0.15556 2893.12548
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:55 0.040 sec 24 0.16638 2489.73957
## 26 2020-06-20 06:43:55 0.041 sec 25 0.17470 2462.83342
## 27 2020-06-20 06:43:55 0.042 sec 26 0.18344 2442.67385
## 28 2020-06-20 06:43:55 0.044 sec 27 0.19261 2433.32061
## 29 2020-06-20 06:43:55 0.046 sec 28 0.20224 2433.02617
## 30 2020-06-20 06:43:55 0.048 sec 29 0.21235 2429.05352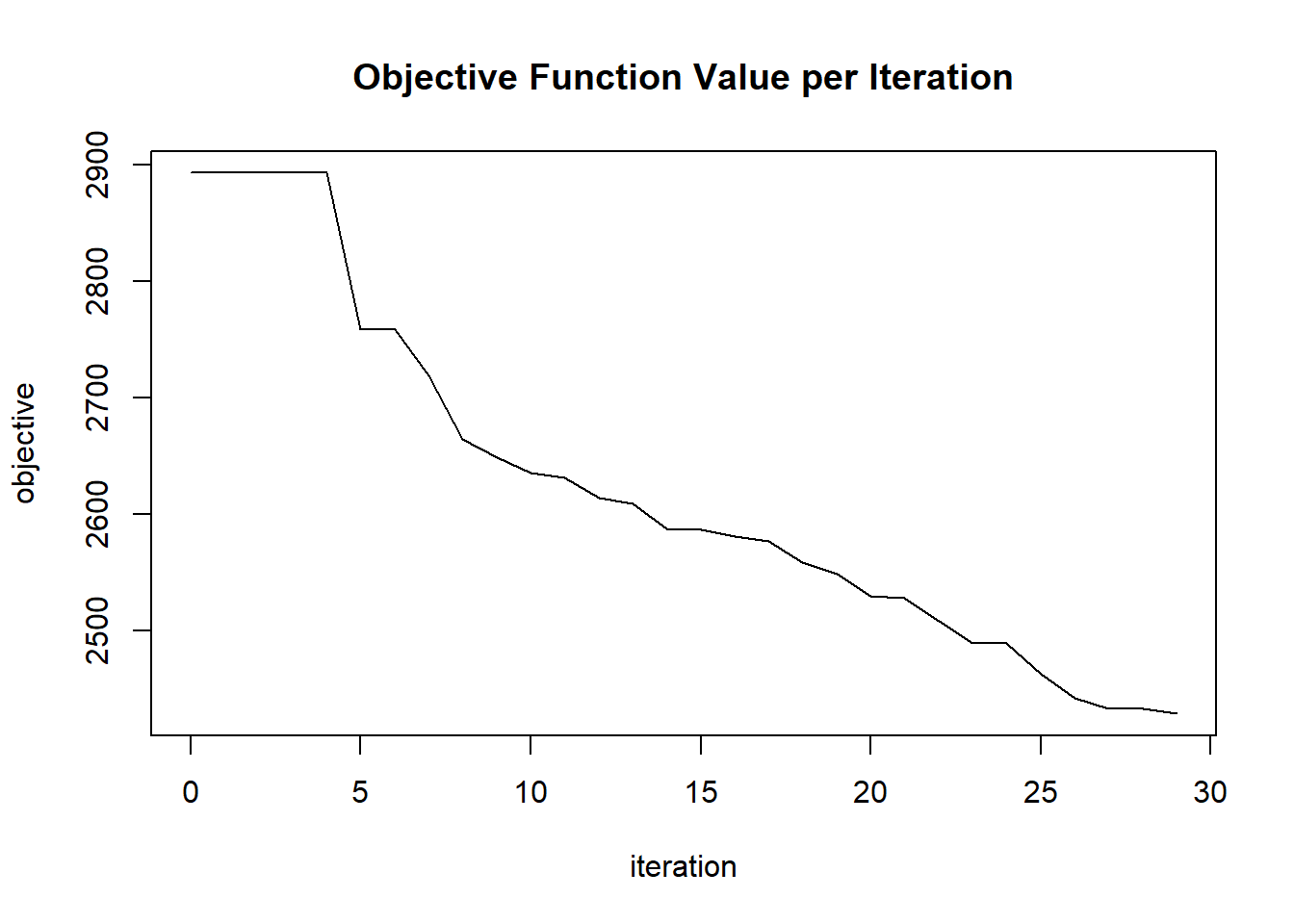
## Iteration 69 of 75 92%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 32 5 Quadratic None 1 0 NA NA
## objective
## 32 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_137
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.13483 1247.99574
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1316.128
## Misclassification Error (Categorical): 131
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:57 0.011 sec 0 1.05000 2225.51619
## 2 2020-06-20 06:43:57 0.013 sec 1 0.70000 2225.51619
## 3 2020-06-20 06:43:57 0.015 sec 2 0.46667 2225.51619
## 4 2020-06-20 06:43:57 0.016 sec 3 0.31111 2225.51619
## 5 2020-06-20 06:43:57 0.018 sec 4 0.15556 2225.51619
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:57 0.050 sec 24 0.16638 1335.45909
## 26 2020-06-20 06:43:57 0.052 sec 25 0.17470 1299.52334
## 27 2020-06-20 06:43:57 0.053 sec 26 0.18344 1277.23156
## 28 2020-06-20 06:43:57 0.055 sec 27 0.12229 1277.23156
## 29 2020-06-20 06:43:57 0.057 sec 28 0.12841 1259.50994
## 30 2020-06-20 06:43:57 0.058 sec 29 0.13483 1247.99574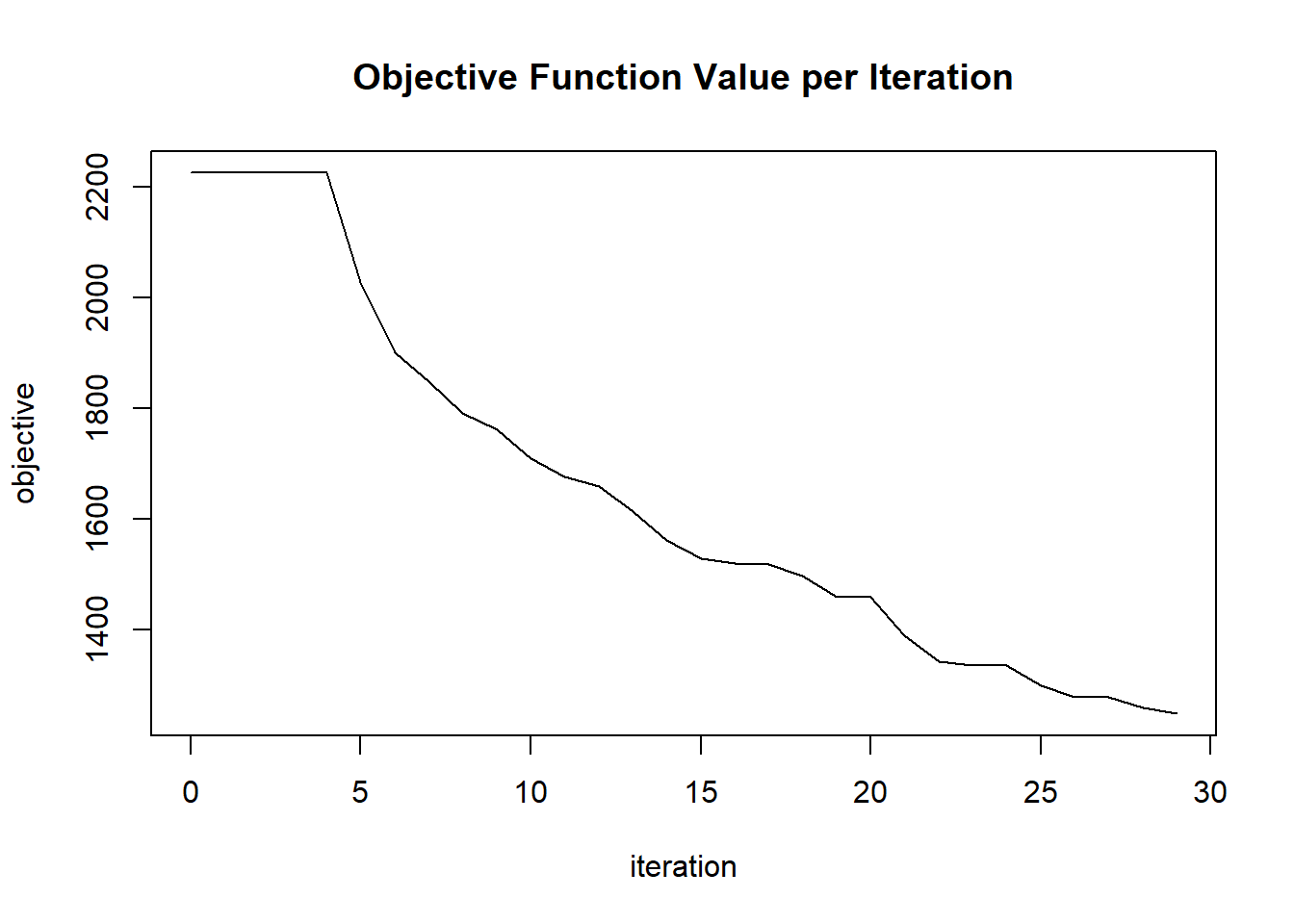
## Iteration 70 of 75 93.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 162 10 L1 L1 4 1 NA NA
## objective
## 162 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_139
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.07247 2253.16831
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1224.258
## Misclassification Error (Categorical): 126
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:43:58 0.017 sec 0 1.05000 4468.41114
## 2 2020-06-20 06:43:58 0.020 sec 1 0.70000 4468.41114
## 3 2020-06-20 06:43:58 0.023 sec 2 0.73500 3772.78952
## 4 2020-06-20 06:43:58 0.026 sec 3 0.49000 3772.78952
## 5 2020-06-20 06:43:58 0.029 sec 4 0.51450 3554.59294
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:43:59 0.093 sec 24 0.08943 2321.43191
## 26 2020-06-20 06:43:59 0.096 sec 25 0.09390 2297.93675
## 27 2020-06-20 06:43:59 0.100 sec 26 0.09860 2281.79156
## 28 2020-06-20 06:43:59 0.103 sec 27 0.06573 2281.79156
## 29 2020-06-20 06:43:59 0.108 sec 28 0.06902 2262.04263
## 30 2020-06-20 06:43:59 0.110 sec 29 0.07247 2253.16831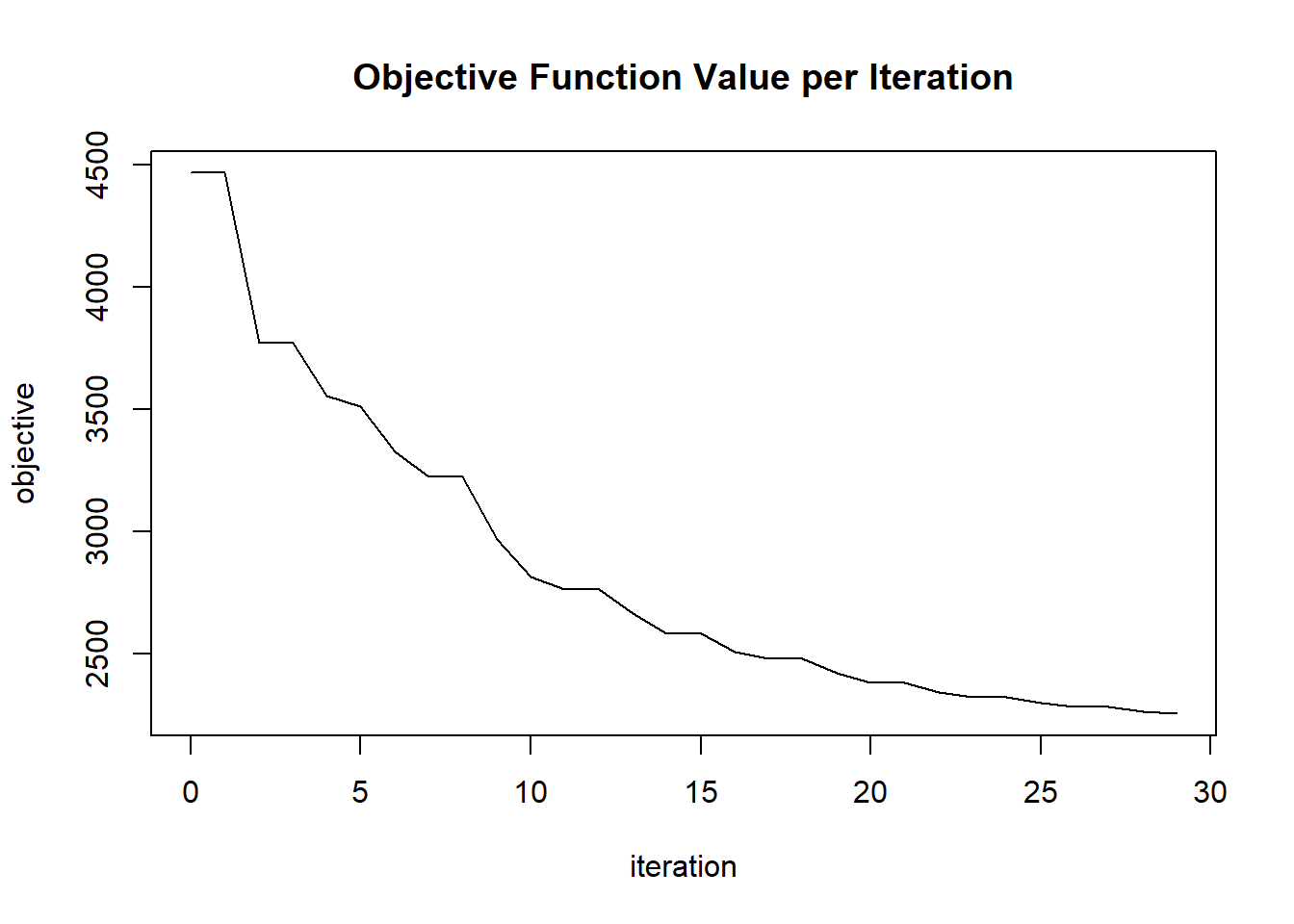
## Iteration 71 of 75 94.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 92 5 None Quadratic 0 1 NA NA
## objective
## 92 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_141
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 1167.80462
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1378.299
## Misclassification Error (Categorical): 109
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:44:00 0.012 sec 0 1.05000 2555.38571
## 2 2020-06-20 06:44:00 0.014 sec 1 0.70000 2555.38571
## 3 2020-06-20 06:44:00 0.016 sec 2 0.46667 2555.38571
## 4 2020-06-20 06:44:00 0.018 sec 3 0.31111 2555.38571
## 5 2020-06-20 06:44:00 0.020 sec 4 0.32667 2452.08664
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:44:00 0.056 sec 24 0.22184 1200.90854
## 26 2020-06-20 06:44:00 0.058 sec 25 0.23294 1193.48888
## 27 2020-06-20 06:44:00 0.060 sec 26 0.15529 1193.48888
## 28 2020-06-20 06:44:00 0.062 sec 27 0.16306 1174.63573
## 29 2020-06-20 06:44:00 0.064 sec 28 0.17121 1170.36713
## 30 2020-06-20 06:44:00 0.066 sec 29 0.17977 1167.80462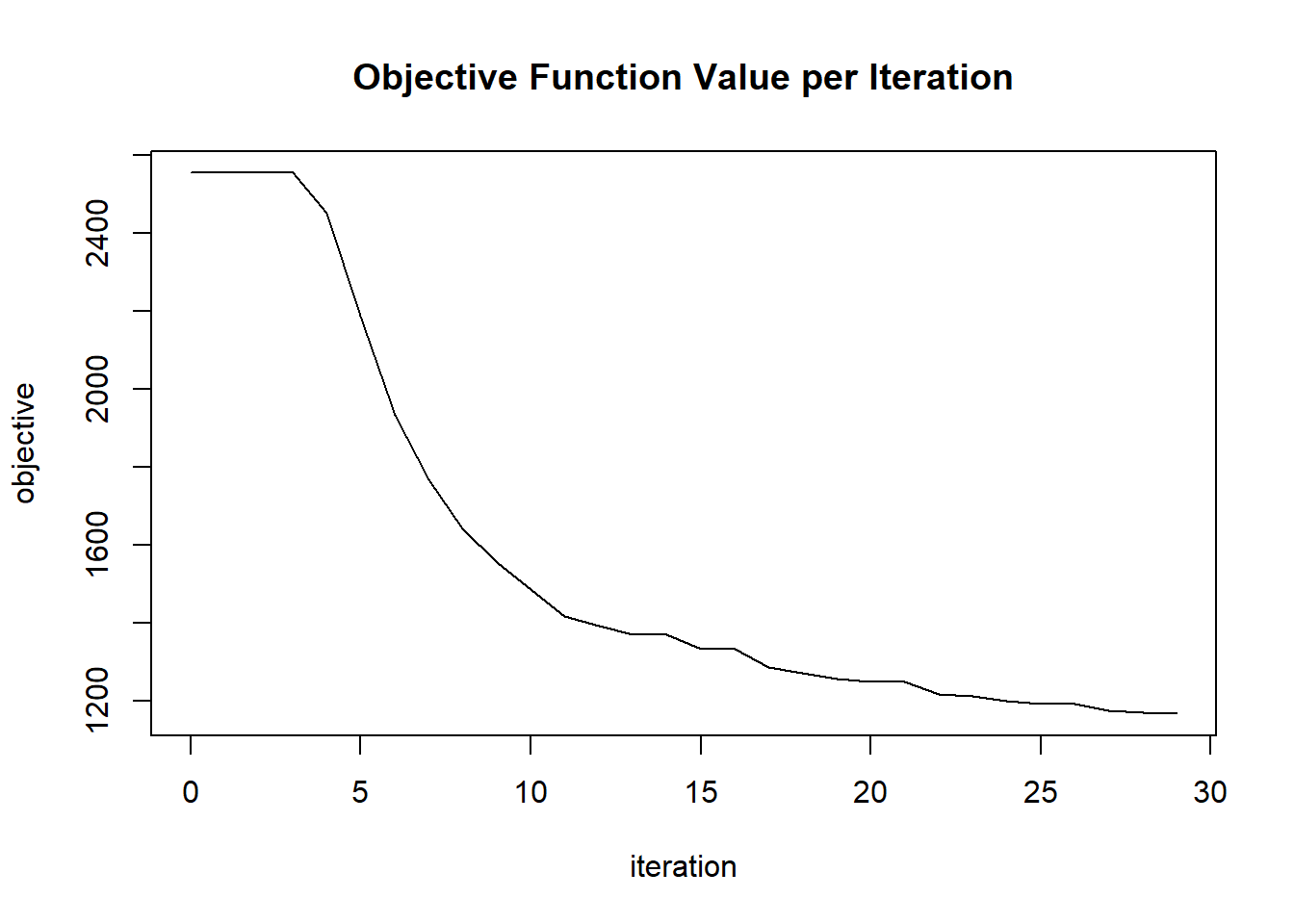
## Iteration 72 of 75 96%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 205 3 L1 Quadratic 1 4 NA NA
## objective
## 205 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_143
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.04601 2459.13423
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1393.852
## Misclassification Error (Categorical): 340
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:44:02 0.009 sec 0 1.05000 3169.78321
## 2 2020-06-20 06:44:02 0.011 sec 1 0.70000 3169.78321
## 3 2020-06-20 06:44:02 0.013 sec 2 0.46667 3169.78321
## 4 2020-06-20 06:44:02 0.014 sec 3 0.49000 3011.45708
## 5 2020-06-20 06:44:02 0.016 sec 4 0.51450 2838.12541
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:44:02 0.043 sec 24 0.08943 2471.16445
## 26 2020-06-20 06:44:02 0.044 sec 25 0.05962 2471.16445
## 27 2020-06-20 06:44:02 0.046 sec 26 0.06260 2468.13156
## 28 2020-06-20 06:44:02 0.047 sec 27 0.06573 2465.87609
## 29 2020-06-20 06:44:02 0.048 sec 28 0.04382 2465.87609
## 30 2020-06-20 06:44:02 0.050 sec 29 0.04601 2459.13423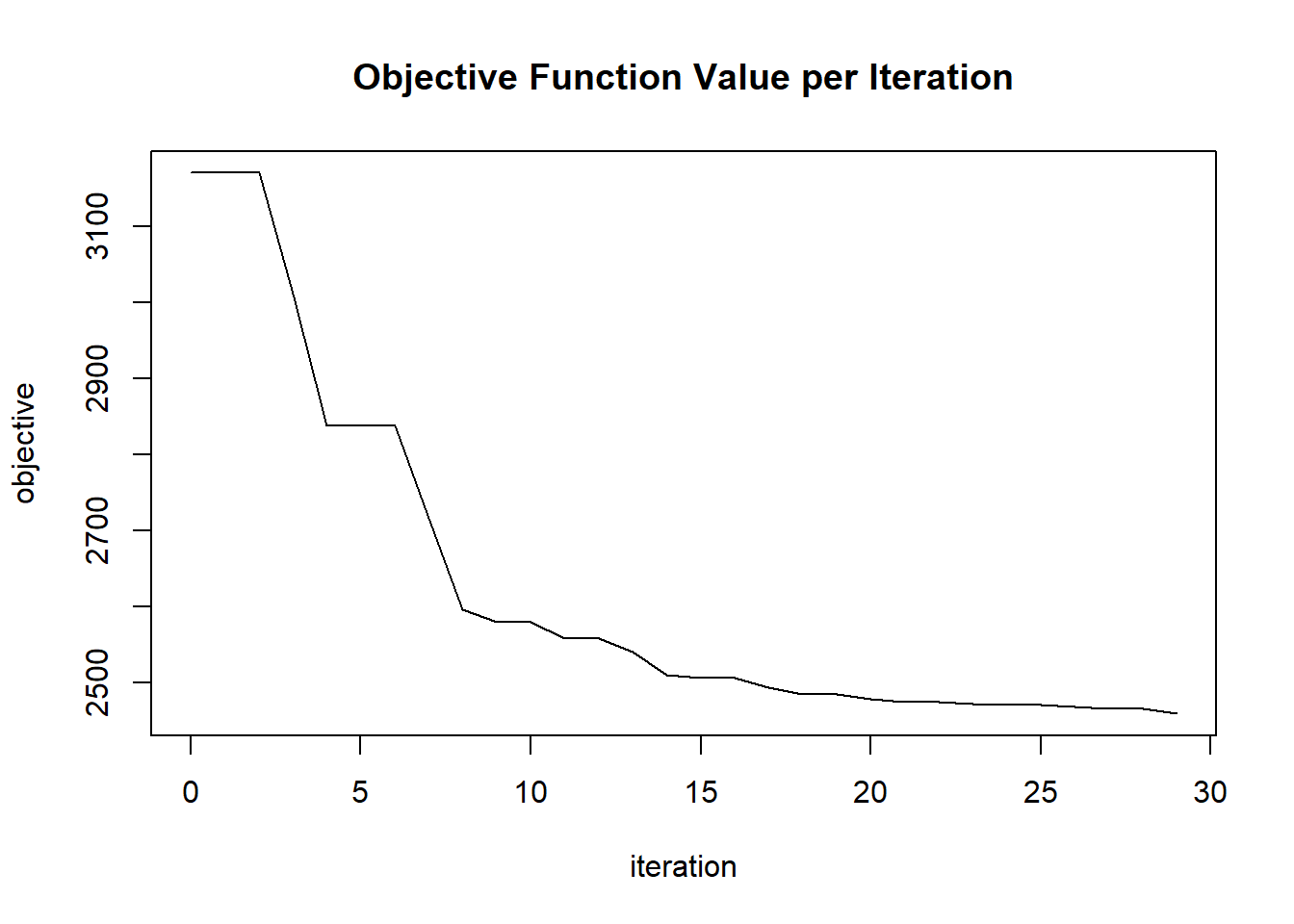
## Iteration 73 of 75 97.3%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 91 3 None Quadratic 0 1 NA NA
## objective
## 91 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_145
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 1869.24089
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 1555.012
## Misclassification Error (Categorical): 257
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:44:03 0.012 sec 0 1.05000 2775.93938
## 2 2020-06-20 06:44:03 0.013 sec 1 0.70000 2775.93938
## 3 2020-06-20 06:44:03 0.015 sec 2 0.46667 2775.93938
## 4 2020-06-20 06:44:03 0.017 sec 3 0.31111 2775.93938
## 5 2020-06-20 06:44:03 0.019 sec 4 0.32667 2725.89448
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:44:03 0.049 sec 24 0.22184 1975.95876
## 26 2020-06-20 06:44:03 0.050 sec 25 0.23294 1930.33840
## 27 2020-06-20 06:44:03 0.052 sec 26 0.24458 1911.34524
## 28 2020-06-20 06:44:03 0.053 sec 27 0.16306 1911.34524
## 29 2020-06-20 06:44:03 0.054 sec 28 0.17121 1880.53655
## 30 2020-06-20 06:44:03 0.056 sec 29 0.17977 1869.24089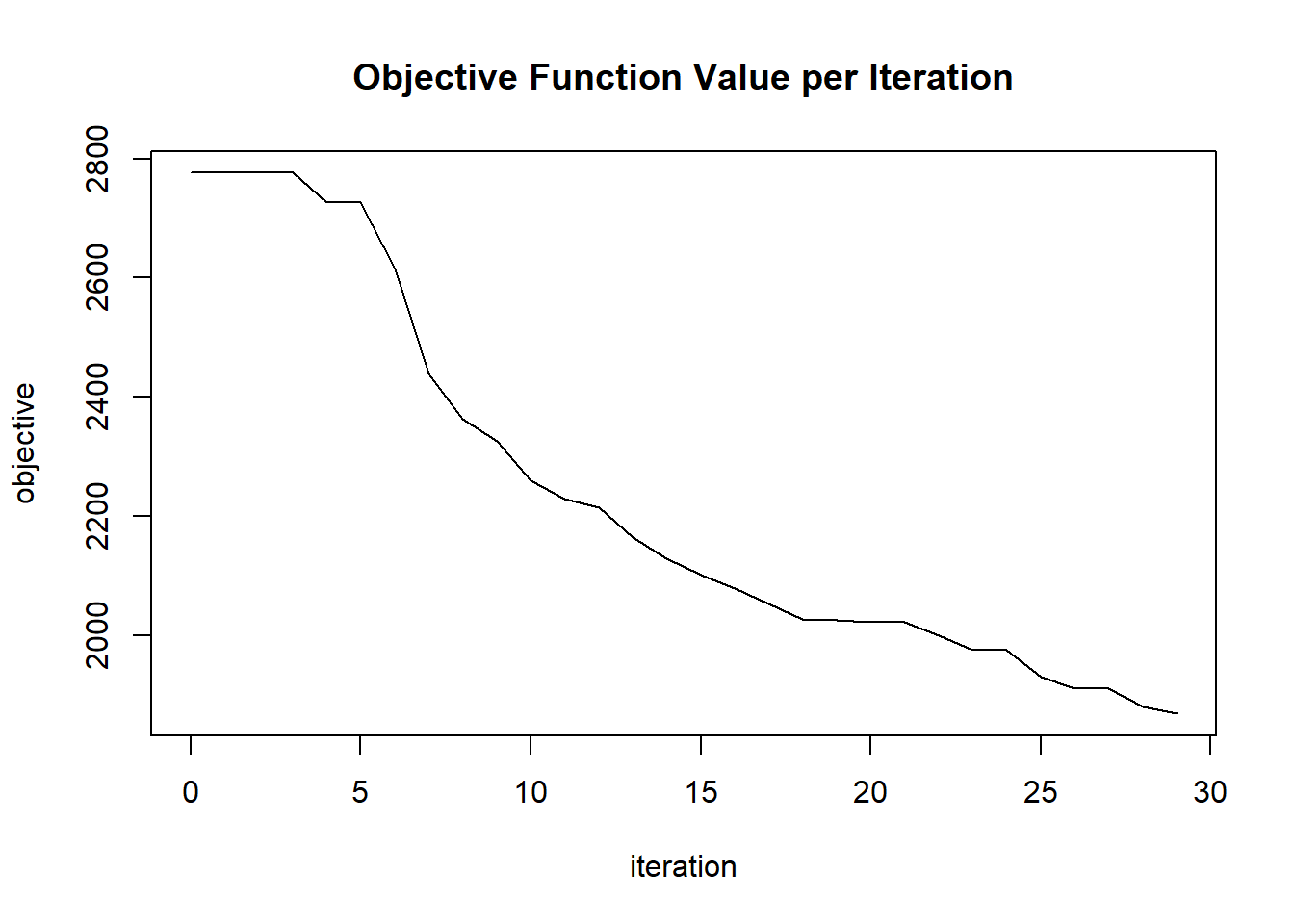
## Iteration 74 of 75 98.7%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 213 10 Quadratic L1 1 4 NA NA
## objective
## 213 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_147
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.17977 1437.09113
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 683.4182
## Misclassification Error (Categorical): 78
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:44:05 0.016 sec 0 1.05000 3652.87841
## 2 2020-06-20 06:44:05 0.019 sec 1 0.70000 3652.87841
## 3 2020-06-20 06:44:05 0.023 sec 2 0.46667 3652.87841
## 4 2020-06-20 06:44:05 0.026 sec 3 0.49000 3124.49085
## 5 2020-06-20 06:44:05 0.029 sec 4 0.51450 2658.24626
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:44:05 0.094 sec 24 0.34941 1485.77762
## 26 2020-06-20 06:44:05 0.097 sec 25 0.23294 1485.77762
## 27 2020-06-20 06:44:05 0.100 sec 26 0.24458 1465.29243
## 28 2020-06-20 06:44:05 0.103 sec 27 0.25681 1451.06874
## 29 2020-06-20 06:44:05 0.106 sec 28 0.17121 1451.06874
## 30 2020-06-20 06:44:05 0.109 sec 29 0.17977 1437.09113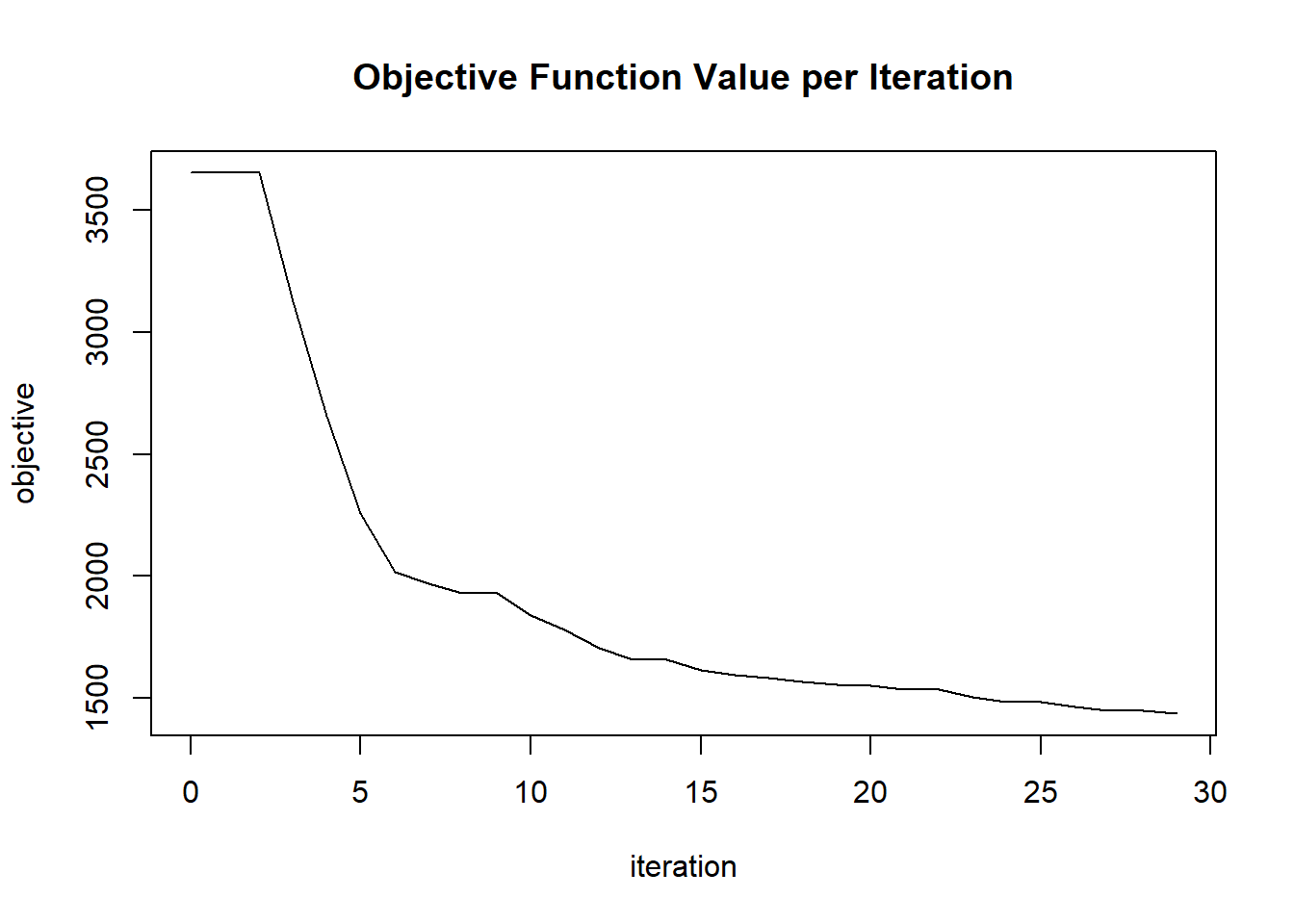
## Iteration 75 of 75 100%
## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 3 10 None None 0 0 NA NA
## objective
## 3 NA
## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: GLRM_model_R_1592660518623_149
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 30 0.28314 369.72868
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 517.8523
## Misclassification Error (Categorical): 15
## Number of Numeric Entries: 1833
## Number of Categorical Entries: 1143
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:44:06 0.016 sec 0 1.05000 3348.56023
## 2 2020-06-20 06:44:06 0.019 sec 1 0.70000 3348.56023
## 3 2020-06-20 06:44:06 0.021 sec 2 0.46667 3348.56023
## 4 2020-06-20 06:44:06 0.024 sec 3 0.31111 3348.56023
## 5 2020-06-20 06:44:06 0.027 sec 4 0.32667 2176.17652
##
## ---
## timestamp duration iterations step_size objective
## 25 2020-06-20 06:44:07 0.085 sec 24 0.34941 427.15184
## 26 2020-06-20 06:44:07 0.088 sec 25 0.36688 424.43268
## 27 2020-06-20 06:44:07 0.091 sec 26 0.24458 424.43268
## 28 2020-06-20 06:44:07 0.095 sec 27 0.25681 385.85102
## 29 2020-06-20 06:44:07 0.098 sec 28 0.26965 378.98067
## 30 2020-06-20 06:44:07 0.102 sec 29 0.28314 369.72868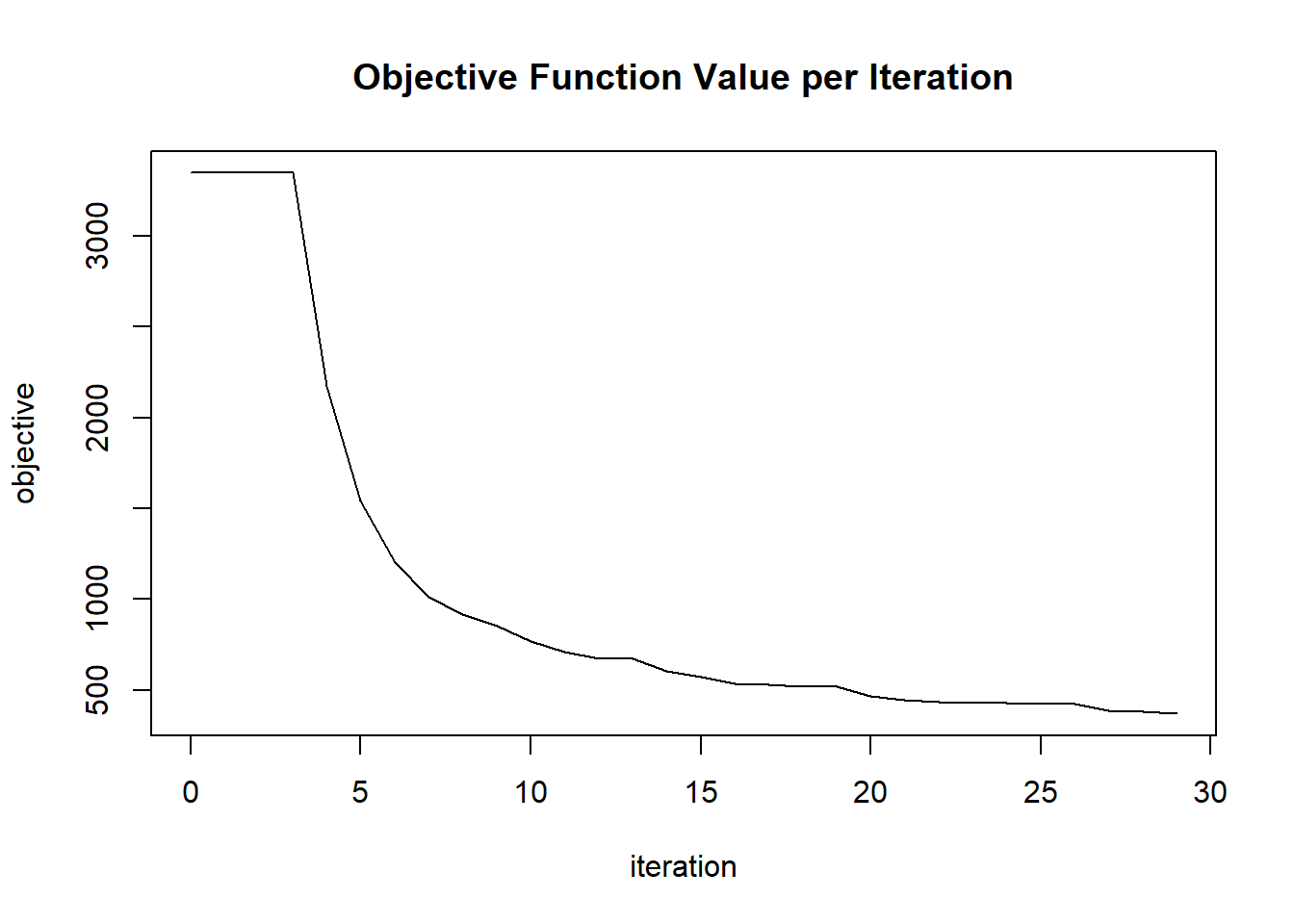
## user system elapsed
## 30.89 0.89 121.45# TODO: confirm that this is correct.
params$error = params$error_num + params$error_cat
save(params, glrm_metrics, glrm_sum,
file = "data/glrm-tuned-results.RData")
qplot(params$error) + theme_minimal() +
labs(x = "Test set error")## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.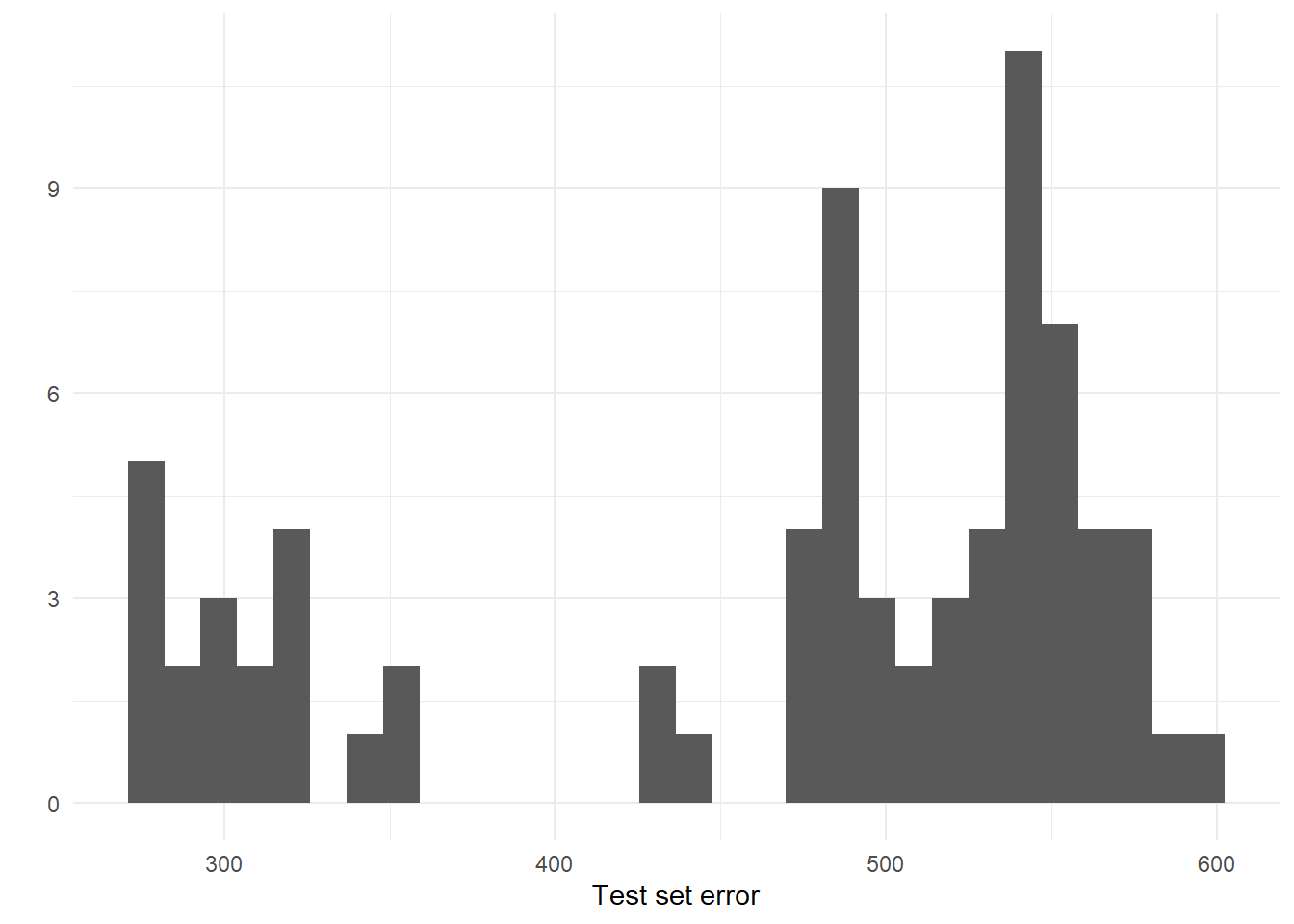
params = params %>% arrange(error) %>% as.data.frame()
# Look at the top 10 models with the lowest error rate
head(params, 25)## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 1 10 Quadratic None 4 0 242.0873 29
## 2 10 None Quadratic 0 1 251.0145 23
## 3 10 Quadratic L1 1 1 250.2923 24
## 4 10 Quadratic L1 4 1 246.7835 29
## 5 10 Quadratic Quadratic 1 1 253.6244 24
## 6 10 None Quadratic 0 4 256.3729 26
## 7 10 None L1 0 1 269.5762 21
## 8 10 Quadratic None 1 0 271.5547 23
## 9 10 L1 Quadratic 1 1 269.3316 26
## 10 10 None None 0 0 282.2528 20
## 11 10 Quadratic L1 1 4 274.0599 31
## 12 10 L1 None 1 0 286.3755 25
## 13 10 L1 L1 1 4 291.9272 26
## 14 10 L1 L1 1 1 293.1568 25
## 15 10 Quadratic Quadratic 4 1 290.1459 32
## 16 10 None L1 0 4 300.5562 24
## 17 10 Quadratic Quadratic 1 4 309.7851 31
## 18 10 L1 Quadratic 1 4 313.1170 36
## 19 10 Quadratic L1 4 4 317.0228 41
## 20 10 Quadratic Quadratic 4 4 384.9836 41
## 21 10 L1 None 4 0 375.8775 54
## 22 10 L1 L1 4 1 394.8270 50
## 23 5 None Quadratic 0 4 410.9857 60
## 24 5 Quadratic None 1 0 418.0738 53
## 25 5 Quadratic None 4 0 402.7778 69
## objective error
## 1 981.6612 271.0873
## 2 673.1549 274.0145
## 3 952.8124 274.2923
## 4 1368.1202 275.7835
## 5 1084.6718 277.6244
## 6 1030.7724 282.3729
## 7 647.6055 290.5762
## 8 681.1118 294.5547
## 9 1439.2804 295.3316
## 10 369.7287 302.2528
## 11 1437.0911 305.0599
## 12 993.9386 311.3755
## 13 1772.0248 317.9272
## 14 1252.3674 318.1568
## 15 1609.3168 322.1459
## 16 970.4729 324.5562
## 17 1608.2907 340.7851
## 18 1928.0001 349.1170
## 19 1911.9792 358.0228
## 20 2299.4429 425.9836
## 21 1959.4131 429.8775
## 22 2253.1683 444.8270
## 23 1482.2927 470.9857
## 24 1247.9957 471.0738
## 25 1479.6458 471.7778## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 51 3 L1 Quadratic 1 1 425.6527 113
## 52 3 Quadratic L1 4 1 422.6933 116
## 53 3 Quadratic None 4 0 422.3144 117
## 54 3 L1 None 1 0 425.7815 115
## 55 3 L1 L1 1 1 425.2071 116
## 56 3 Quadratic Quadratic 1 4 429.4291 112
## 57 5 None L1 0 1 505.9907 36
## 58 3 None Quadratic 0 4 437.1649 105
## 59 3 Quadratic L1 1 4 460.5853 90
## 60 3 None L1 0 1 449.9004 101
## 61 3 Quadratic Quadratic 4 4 437.8739 116
## 62 3 L1 L1 4 1 438.5275 116
## 63 3 L1 Quadratic 1 4 447.8649 107
## 64 3 Quadratic Quadratic 1 1 456.9178 99
## 65 3 Quadratic L1 4 4 442.2654 114
## 66 3 L1 None 4 0 442.6686 116
## 67 5 L1 Quadratic 4 1 462.4949 97
## 68 10 L1 Quadratic 4 4 468.7604 92
## 69 5 L1 L1 4 4 457.1146 107
## 70 5 L1 Quadratic 4 4 464.5910 106
## 71 3 L1 Quadratic 4 1 453.9638 117
## 72 3 None Quadratic 0 1 491.6003 87
## 73 3 None L1 0 4 489.7113 90
## 74 3 L1 L1 4 4 472.2836 116
## 75 3 L1 Quadratic 4 4 472.6318 119
## objective error
## 51 2314.609 538.6527
## 52 2295.969 538.6933
## 53 2137.980 539.3144
## 54 2077.699 540.7815
## 55 2240.163 541.2071
## 56 2382.413 541.4291
## 57 1177.625 541.9907
## 58 2098.792 542.1649
## 59 2429.054 550.5853
## 60 2035.615 550.9004
## 61 2792.101 553.8739
## 62 2572.007 554.5275
## 63 2459.134 554.8649
## 64 2150.624 555.9178
## 65 2652.582 556.2654
## 66 2426.384 558.6686
## 67 2564.772 559.4949
## 68 3097.742 560.7604
## 69 2948.453 564.1146
## 70 3078.152 570.5910
## 71 2719.046 570.9638
## 72 1869.241 578.6003
## 73 2081.980 579.7113
## 74 2928.431 588.2836
## 75 3059.373 591.63183.4.9 Apply best GLRM
params = rio::import("tables/glrm-grid-search.xlsx")
(best_params = params %>% arrange(error) %>% as.data.frame() %>% head(1))## k regularization_x regularization_y gamma_x gamma_y error_num error_cat
## 1 10 Quadratic None 4 0 242.0873 29
## objective error
## 1 981.6612 271.0873system.time({
# Now run on full dataset.
glrm_result =
h2o::h2o.glrm(training_frame = h2o_df, cols = colnames(h2o_df),
loss = "Quadratic",
model_id = "impute_glrm",
seed = 1,
k = best_params$k,
max_iterations = 2000,
# This is necessary to ensure that the model can optimize, otherwise
# there may be no improvement in the objective.
transform = "STANDARDIZE",
regularization_x = best_params$regularization_x,
regularization_y = best_params$regularization_y,
gamma_x = best_params$gamma_x,
gamma_y = best_params$gamma_y,
loss_by_col_idx = losses$index,
loss_by_col = losses$loss)
})## user system elapsed
## 0.12 0.01 2.25## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model Key: impute_glrm
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 237 0.00009 1045.33367
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 864.1832
## Misclassification Error (Categorical): 81
## Number of Numeric Entries: 2397
## Number of Categorical Entries: 1493
##
##
##
## Scoring History:
## timestamp duration iterations step_size objective
## 1 2020-06-20 06:44:13 0.032 sec 0 1.05000 3144.82797
## 2 2020-06-20 06:44:13 0.038 sec 1 0.70000 3144.82797
## 3 2020-06-20 06:44:13 0.044 sec 2 0.46667 3144.82797
## 4 2020-06-20 06:44:13 0.049 sec 3 0.31111 3144.82797
## 5 2020-06-20 06:44:13 0.054 sec 4 0.32667 2931.70821
##
## ---
## timestamp duration iterations step_size objective
## 232 2020-06-20 06:44:15 1.264 sec 231 0.00017 1045.37528
## 233 2020-06-20 06:44:15 1.269 sec 232 0.00011 1045.37528
## 234 2020-06-20 06:44:15 1.274 sec 233 0.00012 1045.34632
## 235 2020-06-20 06:44:15 1.278 sec 234 0.00013 1045.33851
## 236 2020-06-20 06:44:15 1.282 sec 235 0.00013 1045.33367
## 237 2020-06-20 06:44:15 1.287 sec 236 0.00009 1045.33367## Model Details:
## ==============
##
## H2ODimReductionModel: glrm
## Model ID: impute_glrm
## Model Summary:
## number_of_iterations final_step_size final_objective_value
## 1 237 0.00009 1045.33367
##
##
## H2ODimReductionMetrics: glrm
## ** Reported on training data. **
##
## Sum of Squared Error (Numeric): 864.1832
## Misclassification Error (Categorical): 81
## Number of Numeric Entries: 2397
## Number of Categorical Entries: 1493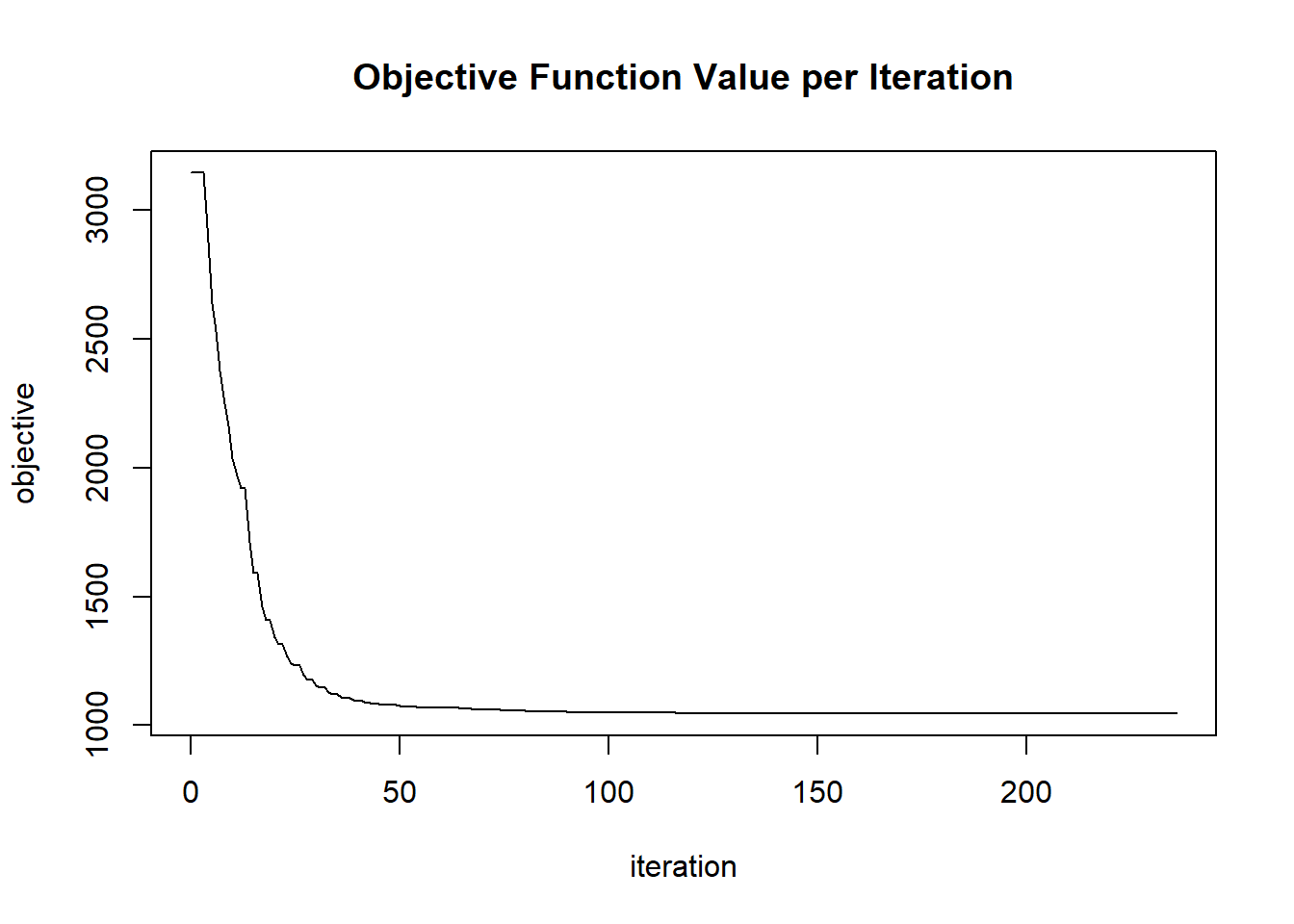
3.4.10 Review GLRM
# Don't use h2o's provided model$importance statistics, they are flawed.
# We need to calculate these manually for now (Apr. 2020).
# Extract compressed dataset.
new_data = as.data.frame(h2o::h2o.getFrame(glrm_result@model$representation_name))
# Calculate variances for each archetype.
(variances = sapply(new_data, stats::var))## Arch1 Arch2 Arch3 Arch4 Arch5 Arch6 Arch7
## 0.02260095 0.02191188 0.02752955 0.02226097 0.02311360 0.02408451 0.02040544
## Arch8 Arch9 Arch10
## 0.01575170 0.03315694 0.02512172## Arch9 Arch3 Arch10 Arch6 Arch5 Arch1 Arch4
## 0.03315694 0.02752955 0.02512172 0.02408451 0.02311360 0.02260095 0.02226097
## Arch2 Arch7 Arch8
## 0.02191188 0.02040544 0.01575170glrm_vars = data.frame(variances, pct_total = variances / sum(variances))
glrm_vars$cumulative_pct = cumsum(glrm_vars$pct_total)
glrm_vars$order = seq(nrow(glrm_vars))
glrm_vars## variances pct_total cumulative_pct order
## Arch9 0.03315694 0.14053286 0.1405329 1
## Arch3 0.02752955 0.11668165 0.2572145 2
## Arch10 0.02512172 0.10647628 0.3636908 3
## Arch6 0.02408451 0.10208015 0.4657710 4
## Arch5 0.02311360 0.09796503 0.5637360 5
## Arch1 0.02260095 0.09579221 0.6595282 6
## Arch4 0.02226097 0.09435124 0.7538794 7
## Arch2 0.02191188 0.09287162 0.8467510 8
## Arch7 0.02040544 0.08648673 0.9332378 9
## Arch8 0.01575170 0.06676223 1.0000000 10data.frame(
component = glrm_vars$order,
PVE = glrm_vars$pct_total,
CVE = glrm_vars$cumulative_pct
) %>%
tidyr::gather(metric, variance_explained, -component) %>%
ggplot(aes(component, variance_explained)) +
geom_point() + theme_minimal() +
facet_wrap(~ metric, ncol = 1, scales = "free")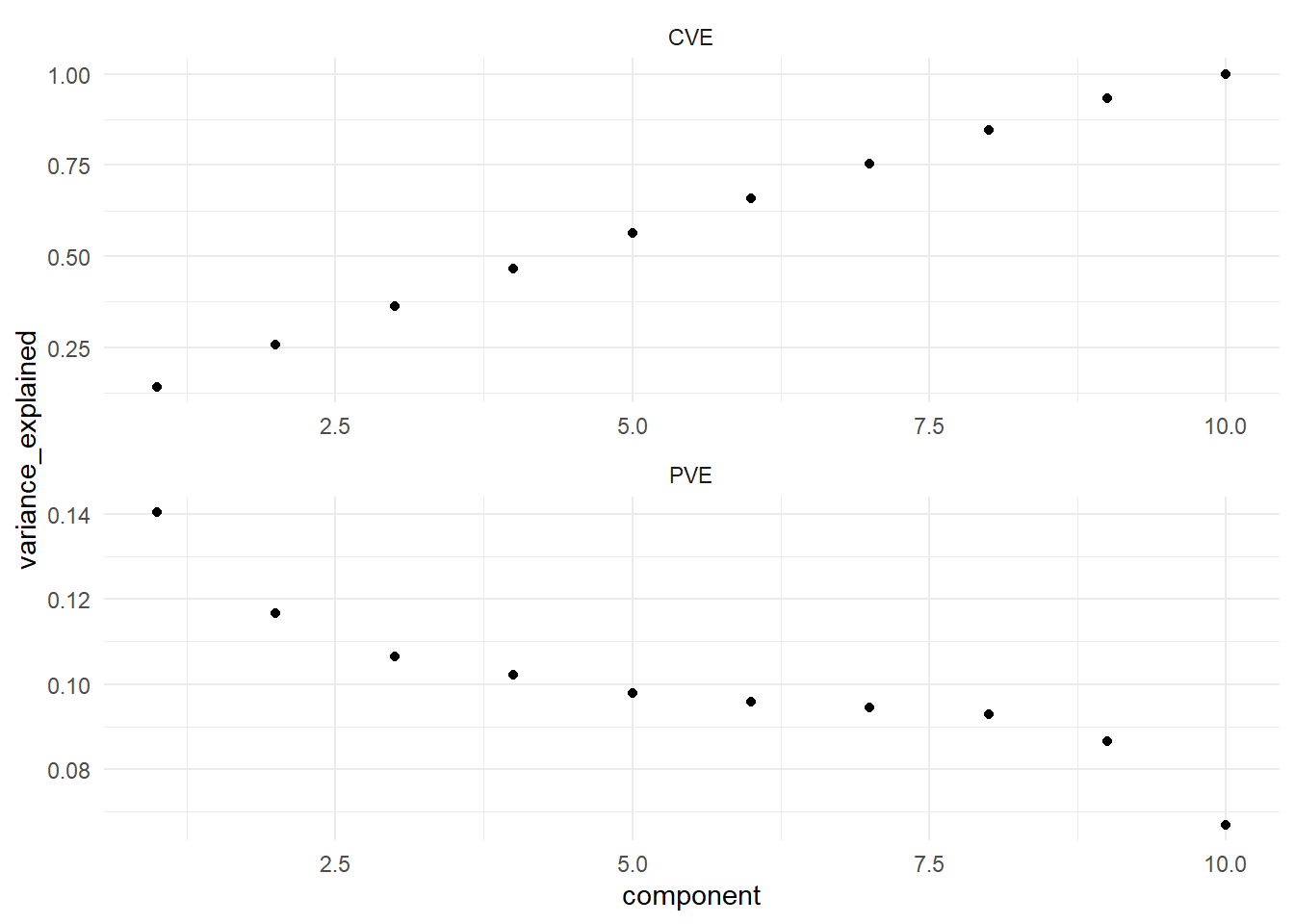
## Saving 7 x 5 in image# Examine how many components (archetypes) to use.
library(dplyr)
library(ggplot2)
# Reconstructed data from GLRM.
recon_df = h2o::h2o.reconstruct(glrm_result, h2o_df,
reverse_transform = TRUE)
# Fix column names.
names(recon_df) = names(impute_df)
# Convert from h2o object back to an R df.
recon_df = as.data.frame(recon_df)
#####################
# Quick quality review on age variable.
# Compare imputed values to known values.
known_age = !is.na(impute_df$age)
# Examine RMSE = 4.3
sqrt(mean((impute_df$age[known_age] - recon_df$age[known_age])^2))## [1] 5.018388# Compare to median imputation, RMSE = 9.1
sqrt(mean((impute_df$age[known_age] - median(impute_df$age[known_age]))^2))## [1] 9.122765# Compare to mean imputation, RMSE = 9.1
sqrt(mean((impute_df$age[known_age] - mean(impute_df$age[known_age]))^2))## [1] 9.0952463.4.11 Evaluate imputation
# TODO: serialize GLRM h2o object for future reference.
# Calculate median/mode imputation for comparison to GLRM.
impute_info =
ck37r::impute_missing_values(data,
# TODO: need to skip date variables, e.g. POSIXct.
# This is yieling an h2o error currently.
skip_vars = c(vars$exclude, vars$outcome),
# Don't add indicators as we've already created those.
add_indicators = FALSE,
type = "standard",
verbose = TRUE)## Found 11 variables with NAs.
## Running standard imputation.
## Imputing age (1 integer) with 5 NAs. Impute value: 55
## Imputing sex (2 factor) with 2 NAs. Impute value: 1
## Imputing cp (3 factor) with 4 NAs. Impute value: 0
## Imputing chol (5 integer) with 3 NAs. Impute value: 240
## Imputing fbs (6 integer) with 4 NAs. Impute value: 0
## Imputing restecg (7 integer) with 5 NAs. Impute value: 1
## Imputing thalach (8 integer) with 3 NAs. Impute value: 152
## Imputing oldpeak (10 numeric) with 7 NAs. Impute value: 0.8
## Imputing slope (11 factor) with 4 NAs. Impute value: 2
## Imputing ca (12 factor) with 6 NAs. Impute value: 0
## Imputing thal (13 factor) with 6 NAs. Impute value: 2# Skip race because it's categorical.
# Also skip the "impute to 0" variables.
(vars_with_missingness =
var_df$var[var_df$missingness > 0 & !var_df$var %in% c("race") &
!var_df$var %in% impute_to_0_vars])## [1] "ca" "oldpeak" "restecg" "slope" "age" "sex" "cp"
## [8] "thal" "thalach" "chol" "fbs"# Bound GLRM variables back to the original bounds.
for (var in vars_with_missingness) {
row = var_df[var_df$var == var, , drop = FALSE]
# Skip factor vars.
if (row$class != "factor") {
recon_df[[var]] = pmin(pmax(recon_df[[var]], row$min), row$max)
}
}
# Round integer and ordinal vars back to be integers.
for (var in c(vars$integers, vars$ordinal)) {
# TODO: confirm if we need both round() and as.integer() here.
recon_df[[var]] = as.integer(round(recon_df[[var]]))
}
# Loop over each variable and compare GLRM imputation to median/mode imputation
# Use RMSE as a comparison metric.
# TODO: use a training/test split to make this kosher.
impute_compare = data.frame(var = vars_with_missingness,
loss = losses[var_df$var %in% vars_with_missingness, "loss"],
missingness = var_df[var_df$var %in% vars_with_missingness, "missingness"],
error_glrm = NA,
error_median = NA,
pct_reduction = NA,
stringsAsFactors = FALSE)
# TODO: get this to work with categorical variables.
# For now, remove categorical variables.
#(impute_compare = subset(impute_compare, loss != "Categorical"))
for (var in impute_compare$var) {
# Obesity became a factor?
cat("Analzying", var, class(data[[var]]), class(recon_df[[var]]), "\n")
# Analyze the rows in which the variable is not missing.
observed_rows = !is.na(data[[var]])
# Calculate RMSE for GLRM.
error_glrm = sqrt(mean((impute_df[observed_rows, var] -
recon_df[observed_rows, var])^2))
# Compare to median imputation.
error_median = sqrt(mean((impute_df[observed_rows, var] -
impute_info$impute_values[[var]])^2))
# Save results
impute_compare[impute_compare$var == var,
c("error_glrm", "error_median")] = c(error_glrm, error_median)
}## Analzying ca factor factor## Warning in Ops.factor(impute_df[observed_rows, var], recon_df[observed_rows, :
## '-' not meaningful for factors## Warning in Ops.factor(impute_df[observed_rows, var],
## impute_info$impute_values[[var]]): '-' not meaningful for factors## Analzying oldpeak numeric numeric
## Analzying restecg integer numeric
## Analzying slope factor factor## Warning in Ops.factor(impute_df[observed_rows, var], recon_df[observed_rows, :
## '-' not meaningful for factors
## Warning in Ops.factor(impute_df[observed_rows, var], recon_df[observed_rows, :
## '-' not meaningful for factors## Analzying age integer numeric
## Analzying sex factor factor## Warning in Ops.factor(impute_df[observed_rows, var], recon_df[observed_rows, :
## '-' not meaningful for factors
## Warning in Ops.factor(impute_df[observed_rows, var], recon_df[observed_rows, :
## '-' not meaningful for factors## Analzying cp factor factor## Warning in Ops.factor(impute_df[observed_rows, var], recon_df[observed_rows, :
## '-' not meaningful for factors
## Warning in Ops.factor(impute_df[observed_rows, var], recon_df[observed_rows, :
## '-' not meaningful for factors## Analzying thal factor factor## Warning in Ops.factor(impute_df[observed_rows, var], recon_df[observed_rows, :
## '-' not meaningful for factors
## Warning in Ops.factor(impute_df[observed_rows, var], recon_df[observed_rows, :
## '-' not meaningful for factors## Analzying thalach integer numeric
## Analzying chol integer numeric
## Analzying fbs integer numericimpute_compare$pct_reduction = 1 - impute_compare$error_glrm / impute_compare$error_median
(impute_compare = impute_compare %>% arrange(desc(missingness)) %>% as.data.frame())## var loss missingness error_glrm error_median pct_reduction
## 1 oldpeak Huber 0.02310231 0.78744295 1.1901624 0.3383735
## 2 ca Categorical 0.01980198 NA NA NA
## 3 thal Categorical 0.01980198 NA NA NA
## 4 restecg Huber 0.01650165 0.16977460 0.7071068 0.7599025
## 5 age Huber 0.01650165 5.01838842 9.1227645 0.4499049
## 6 slope Categorical 0.01320132 NA NA NA
## 7 cp Categorical 0.01320132 NA NA NA
## 8 fbs Huber 0.01320132 0.09768869 0.3879455 0.7481896
## 9 thalach Huber 0.00990099 16.00993723 22.8834729 0.3003712
## 10 chol Huber 0.00990099 37.75530167 52.2104715 0.2768634
## 11 sex Categorical 0.00660066 NA NA NAcat("Average percent reduction in RMSE:",
round(100 * mean(impute_compare$pct_reduction, na.rm = TRUE), 1), "\n")## Average percent reduction in RMSE: 47.9save(impute_compare, file = "data/imputation-comparison-glrm.RData")
# Make a separate copy for use in the paper.
imput_comp = impute_compare
imput_comp$pct_reduction = round(imput_comp$pct_reduction * 100, 2)
imput_comp$missingness = round(imput_comp$missingness * 100, 2)
# Remove loss column.
imput_comp$loss = NULL
names(imput_comp) = c("Variable", "Missingness", "Error GLRM", "Error Median", "Percent reduction")
(kab_table = kable(imput_comp, format = "latex", digits = c(1, 1, 3, 3, 1),
caption = "Comparing missing value imputation using GLRM versus median/mode",
label = "imputation-comparison",
booktabs = TRUE))3.4.12 Replace missing values.
# Now replace the missing values with imputed values.
for (var in impute_compare$var) {
# Analyze the rows in which the variable is not missing.
missing_rows = is.na(data[[var]])
data[missing_rows, var] = recon_df[missing_rows, var]
}
# Should be all 0's.
summary(colMeans(is.na(data)))## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0 0 0 0 0 0## age sex cp trestbps chol fbs restecg thalach
## 0 0 0 0 0 0 0 0
## exang oldpeak slope ca thal
## 0 0 0 0 0## [1] "age" "sex" "cp" "trestbps" "chol"
## [6] "fbs" "restecg" "thalach" "exang" "oldpeak"
## [11] "slope" "ca" "thal" "target" "miss_age"
## [16] "miss_sex" "miss_cp" "miss_chol" "miss_fbs" "miss_restecg"
## [21] "miss_thalach" "miss_exang" "miss_oldpeak" "miss_slope" "miss_ca"
## [26] "miss_thal"# Update the predictors with the new missingness indicators.
(vars$predictors = setdiff(names(data), c(vars$exclude, vars$outcomes)))## [1] "age" "sex" "cp" "trestbps" "chol"
## [6] "fbs" "restecg" "thalach" "exang" "oldpeak"
## [11] "slope" "ca" "thal" "miss_age" "miss_sex"
## [16] "miss_cp" "miss_chol" "miss_fbs" "miss_restecg" "miss_thalach"
## [21] "miss_exang" "miss_oldpeak" "miss_slope" "miss_ca" "miss_thal"## age sex cp trestbps chol fbs
## 0 0 0 0 0 0
## restecg thalach exang oldpeak slope ca
## 0 0 0 0 0 0
## thal target miss_age miss_sex miss_cp miss_chol
## 0 0 0 0 0 0
## miss_fbs miss_restecg miss_thalach miss_exang miss_oldpeak miss_slope
## 0 0 0 0 0 0
## miss_ca miss_thal
## 0 03.5 Update predictor summary
## Var: fbs
##
## 0 0.0771160802470997 0.170076509369194 0.363667408225791
## 255 1 1 1
## 1
## 45
## Var: restecg
##
## 0 0.276255291712452 0.620070370142201 0.66372197263869
## 146 1 1 1
## 0.950072559816494 1 1.19642276841703 2
## 1 149 1 33.6 Histogram condense
Apply histogram condensing to high-cardinality features
uniq_val_threshold = 80L
# These are the continuous vars with moderate or high missingness.
(dense_vars = var_df[var_df$uniq_vals > uniq_val_threshold, c("var", "uniq_vals")])## var uniq_vals
## 10 thalach 93
## 11 chol 155hist_bins = uniq_val_threshold
for (dense_var in dense_vars$var) {
# Confirm it has a large number of unique values.
num_unique = length(unique(data[[dense_var]]))
if (num_unique > uniq_val_threshold) {
print(qplot(data[[dense_var]]) + theme_minimal() +
labs(x = dense_var, y = "original values"))
# Try histogram binning vs. equal-sized group binning.
hist_vec2 = histogram::histogram(data[[dense_var]],
control = list(maxbin = hist_bins))
# Apply histogram binning to original data vector.
cuts = cut(data[[dense_var]], breaks = hist_vec2$breaks,
# If we don't specify this, all obs with lowest value will get an NA.
include.lowest = TRUE)
# Use the midpoint of each bin as the new value.
mid_vals = hist_vec2$mids[as.numeric(cuts)]
# Check for missing values in the dense vars.
if (sum(is.na(mid_vals)) > 0) {
stop("missing values in mid_vals")
}
# Update variable to use the mid_vals
data[[dense_var]] = mid_vals
print(qplot(mid_vals) + labs(x = dense_var, y = "mid_vals") + theme_minimal())
}
}## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.## Choosing between regular and irregular histogram:
##
## 1.Building regular histogram with maximum number of bins 53.
## - Choosing number of bins via maximum likelihood with BR penalty.
## - Number of bins chosen: 10.
##
##
## 2.Building irregular histogram.
## - Using finest grid based on observations.
## - Choosing number of bins via maximum likelihood with PENB penalty.
## - Computing weights for dynamic programming algorithm.
## - Now performing dynamic optimization.
## - Number of bins chosen: 4.
##
##
##
## Regular histogram chosen.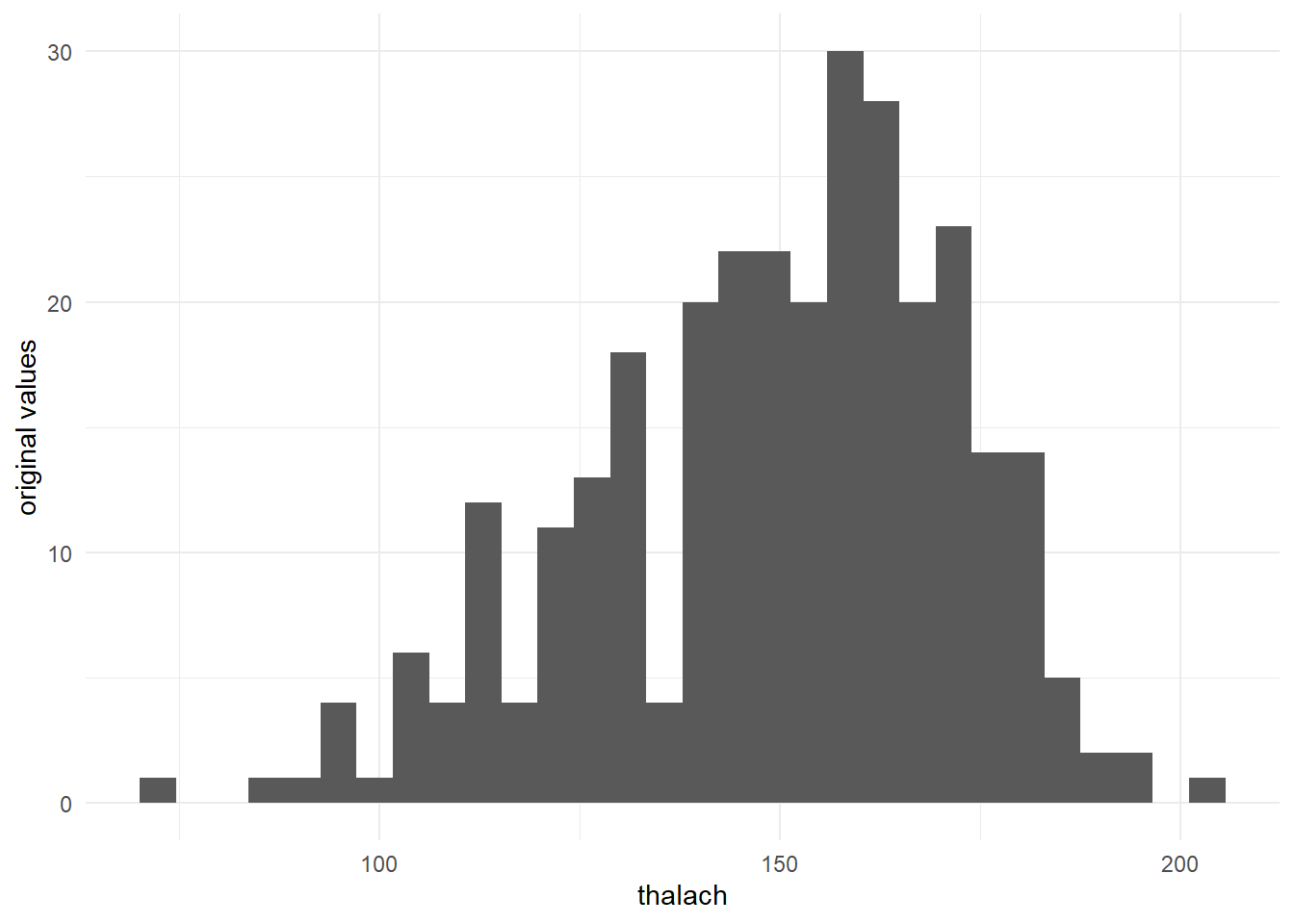
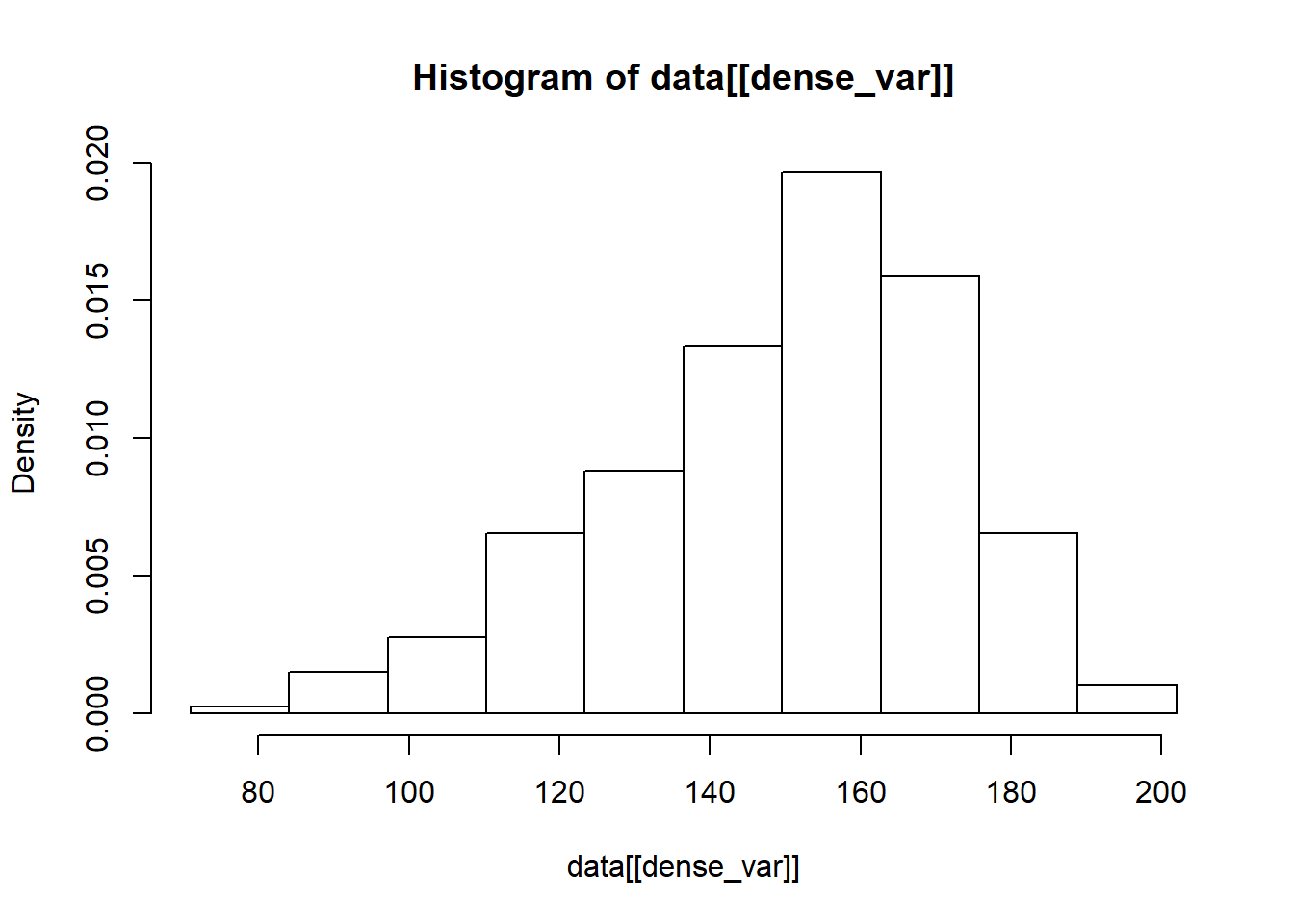
## $breaks
## [1] 71.0 84.1 97.2 110.3 123.4 136.5 149.6 162.7 175.8 188.9 202.0
##
## $counts
## [1] 1 6 11 26 35 53 78 63 26 4
##
## $density
## [1] 0.0002519336 0.0015116015 0.0027712695 0.0065502733 0.0088176757
## [6] 0.0133524803 0.0196508200 0.0158718162 0.0065502733 0.0010077344
##
## $mids
## [1] 77.55 90.65 103.75 116.85 129.95 143.05 156.15 169.25 182.35 195.45
##
## $xname
## [1] "data[[dense_var]]"
##
## $equidist
## [1] TRUE
##
## attr(,"class")
## [1] "histogram"## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.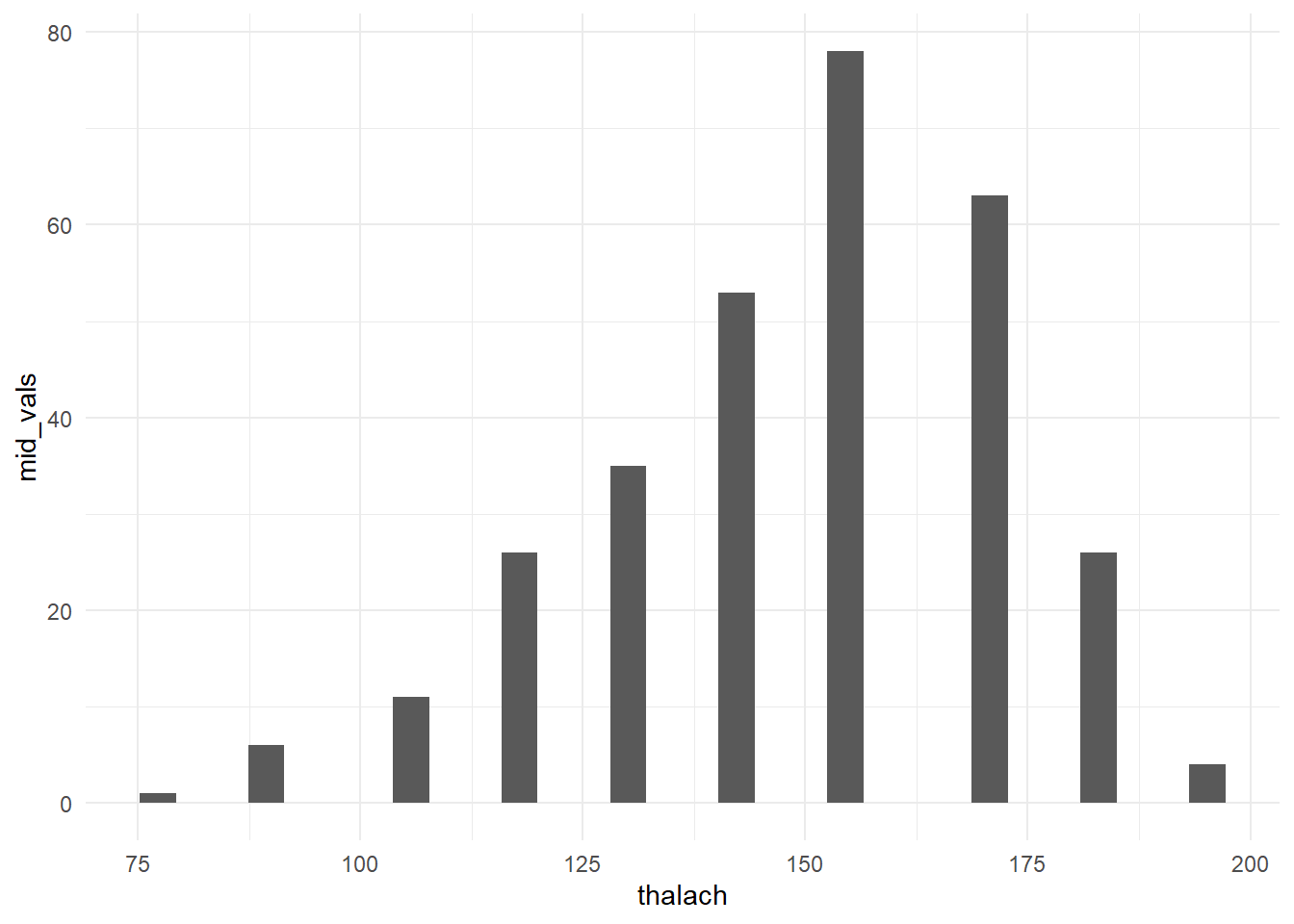
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Choosing between regular and irregular histogram:
##
## 1.Building regular histogram with maximum number of bins 53.
## - Choosing number of bins via maximum likelihood with BR penalty.
## - Number of bins chosen: 9.
##
##
## 2.Building irregular histogram.
## - Using finest grid based on observations.
## - Choosing number of bins via maximum likelihood with PENB penalty.
## - Using greedy procedure to recursively build a finest partition with at most 100 bins.
## - Pre-selected finest partition with 100 bins.
## - Computing weights for dynamic programming algorithm.
## - Now performing dynamic optimization.
## - Number of bins chosen: 5.
##
##
##
## Regular histogram chosen.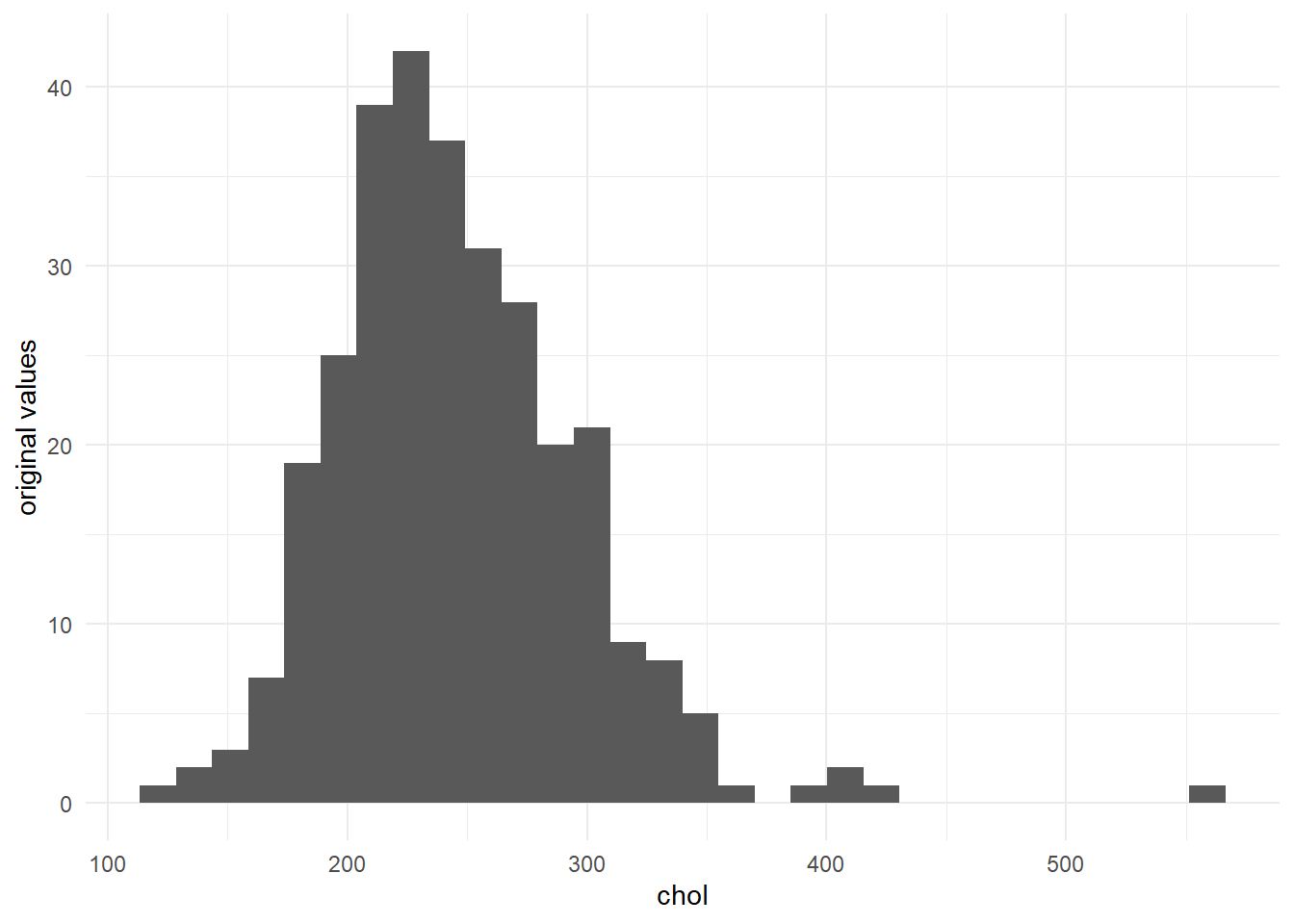
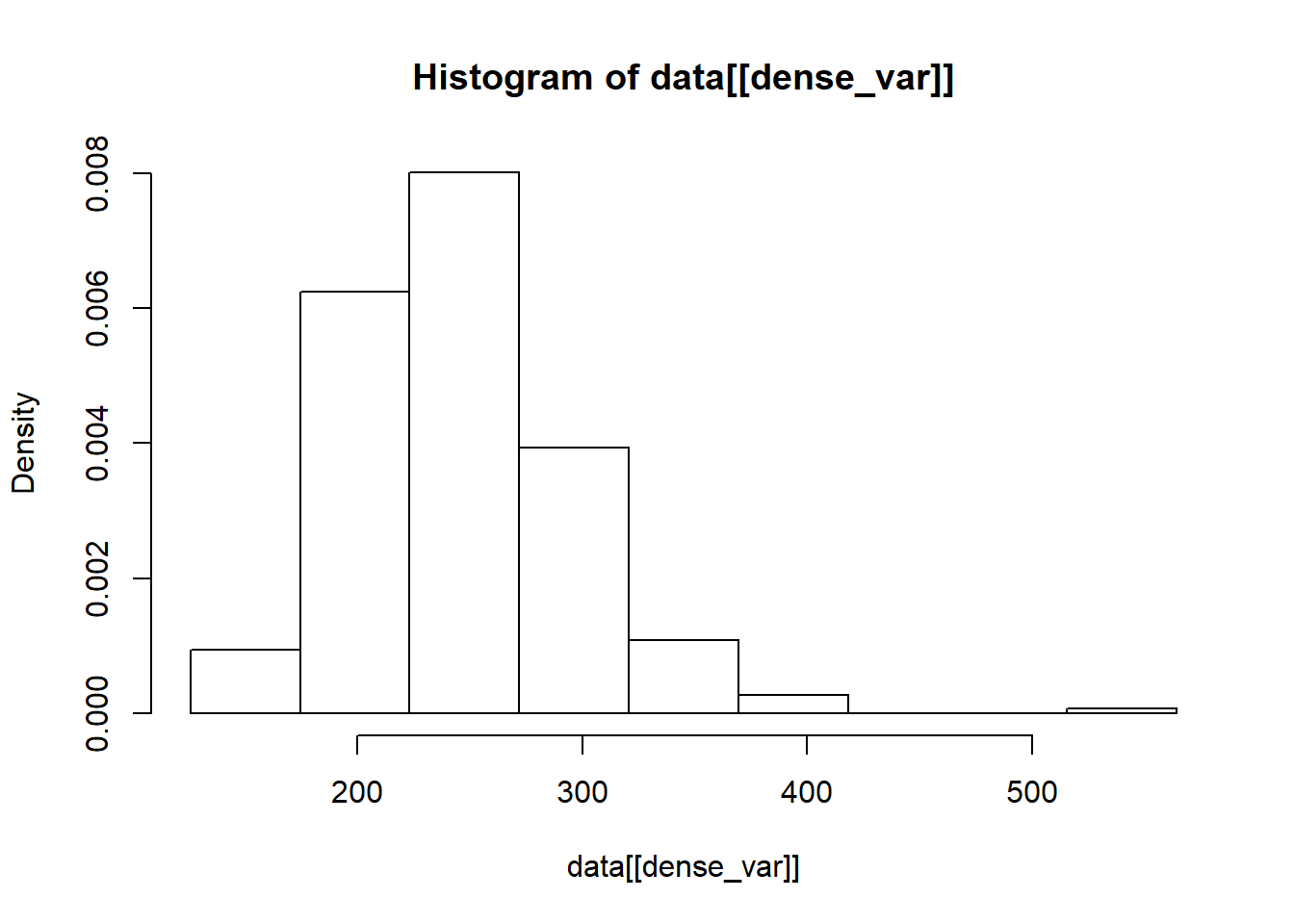
## $breaks
## [1] 126.0000 174.6667 223.3333 272.0000 320.6667 369.3333 418.0000 466.6667
## [9] 515.3333 564.0000
##
## $counts
## [1] 14 92 118 58 16 4 0 0 1
##
## $density
## [1] 0.000949410 0.006238980 0.008002170 0.003933270 0.001085040 0.000271260
## [7] 0.000000000 0.000000000 0.000067815
##
## $mids
## [1] 150.3333 199.0000 247.6667 296.3333 345.0000 393.6667 442.3333 491.0000
## [9] 539.6667
##
## $xname
## [1] "data[[dense_var]]"
##
## $equidist
## [1] TRUE
##
## attr(,"class")
## [1] "histogram"## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.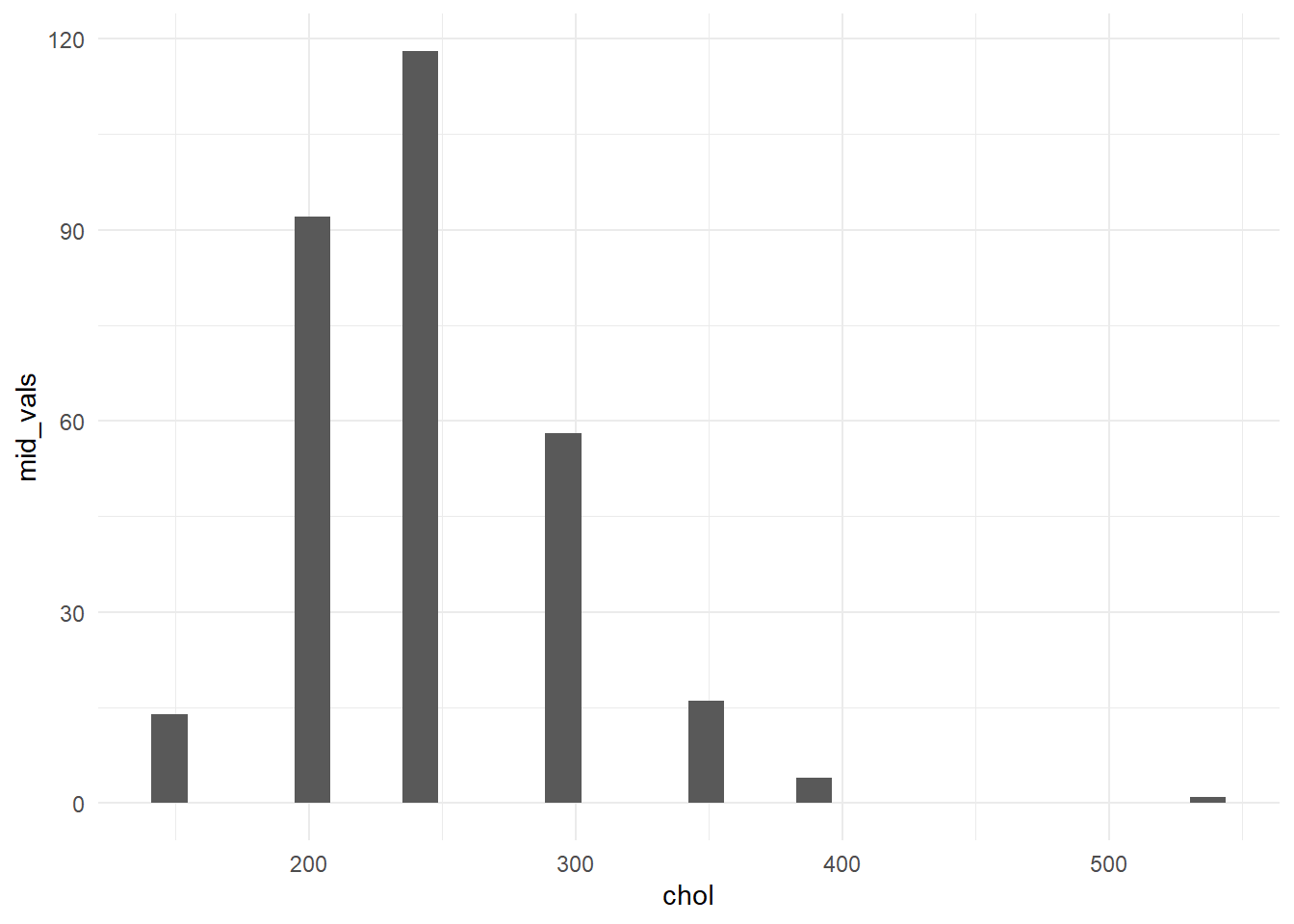
## thalach chol
## 0 03.7 Update predictor summary
## Var: chol
##
## 150.333333333333 199 247.666666666667 296.333333333333
## 14 92 118 58
## 345 393.666666666667 539.666666666667
## 16 4 1
## Var: fbs
##
## 0 0.0771160802470997 0.170076509369194 0.363667408225791
## 255 1 1 1
## 1
## 45
## Var: restecg
##
## 0 0.276255291712452 0.620070370142201 0.66372197263869
## 146 1 1 1
## 0.950072559816494 1 1.19642276841703 2
## 1 149 1 3
## Var: thalach
##
## 77.55 90.65 103.75 116.85 129.95 143.05 156.15 169.25 182.35 195.45
## 1 6 11 26 35 53 78 63 26 4